Institute of Mechanics,
Chinese Academy of Sciences
2021 Vol.11(3)
Theoretical and Applied Mechanics Letters 11 (2021) 100241.
doi: 10.1016/j.taml.2021.100241
Abstract:
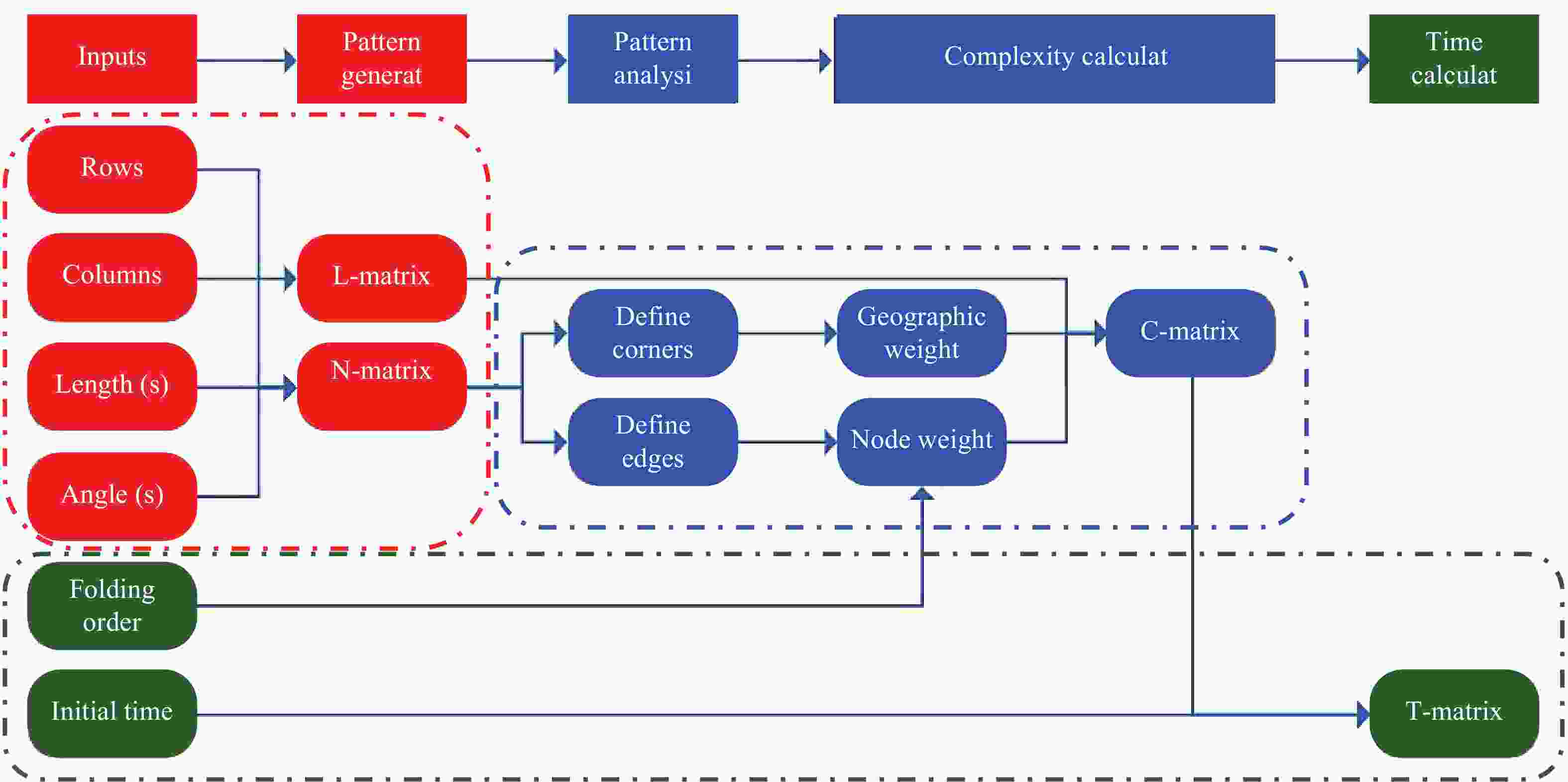
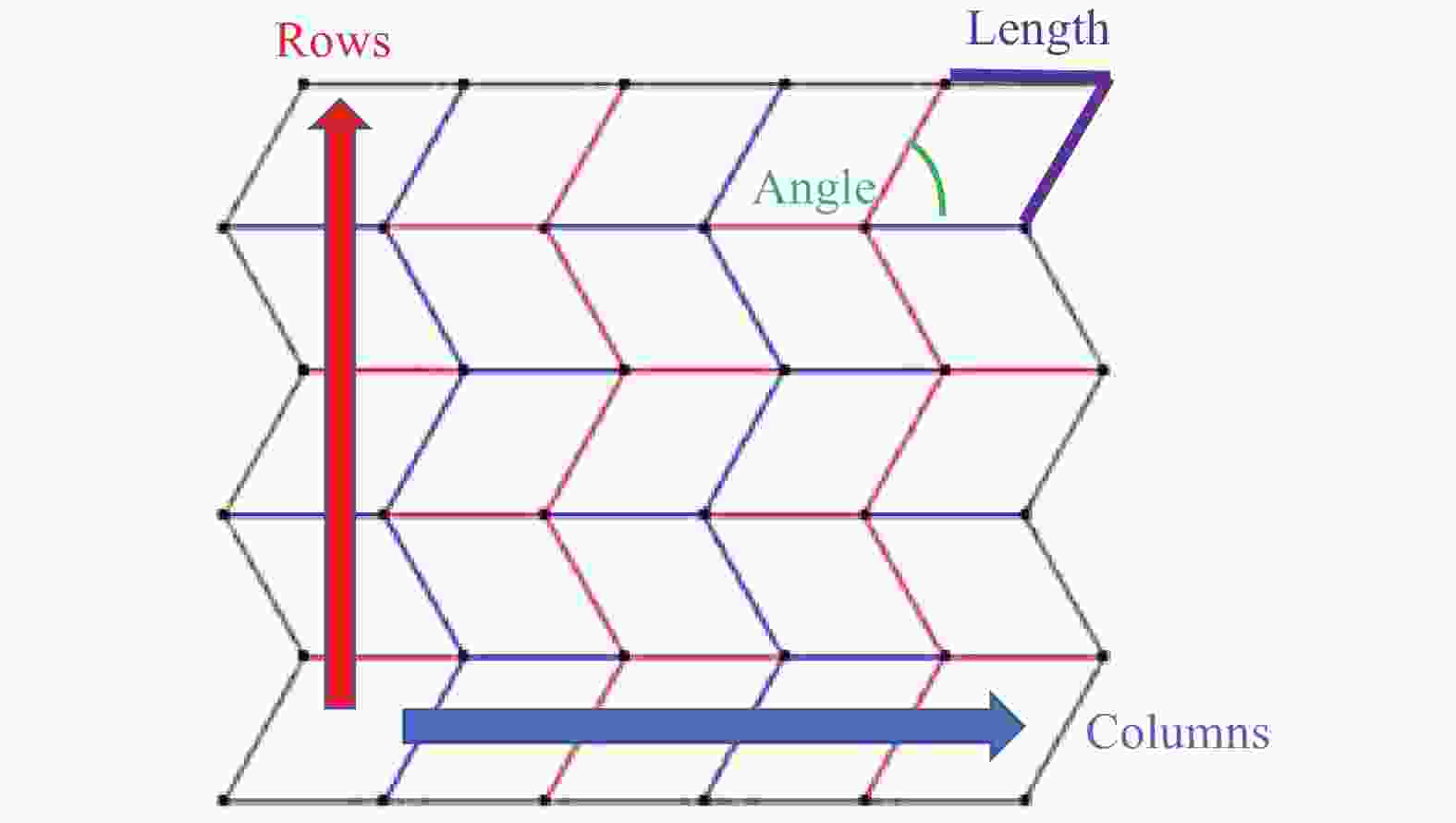
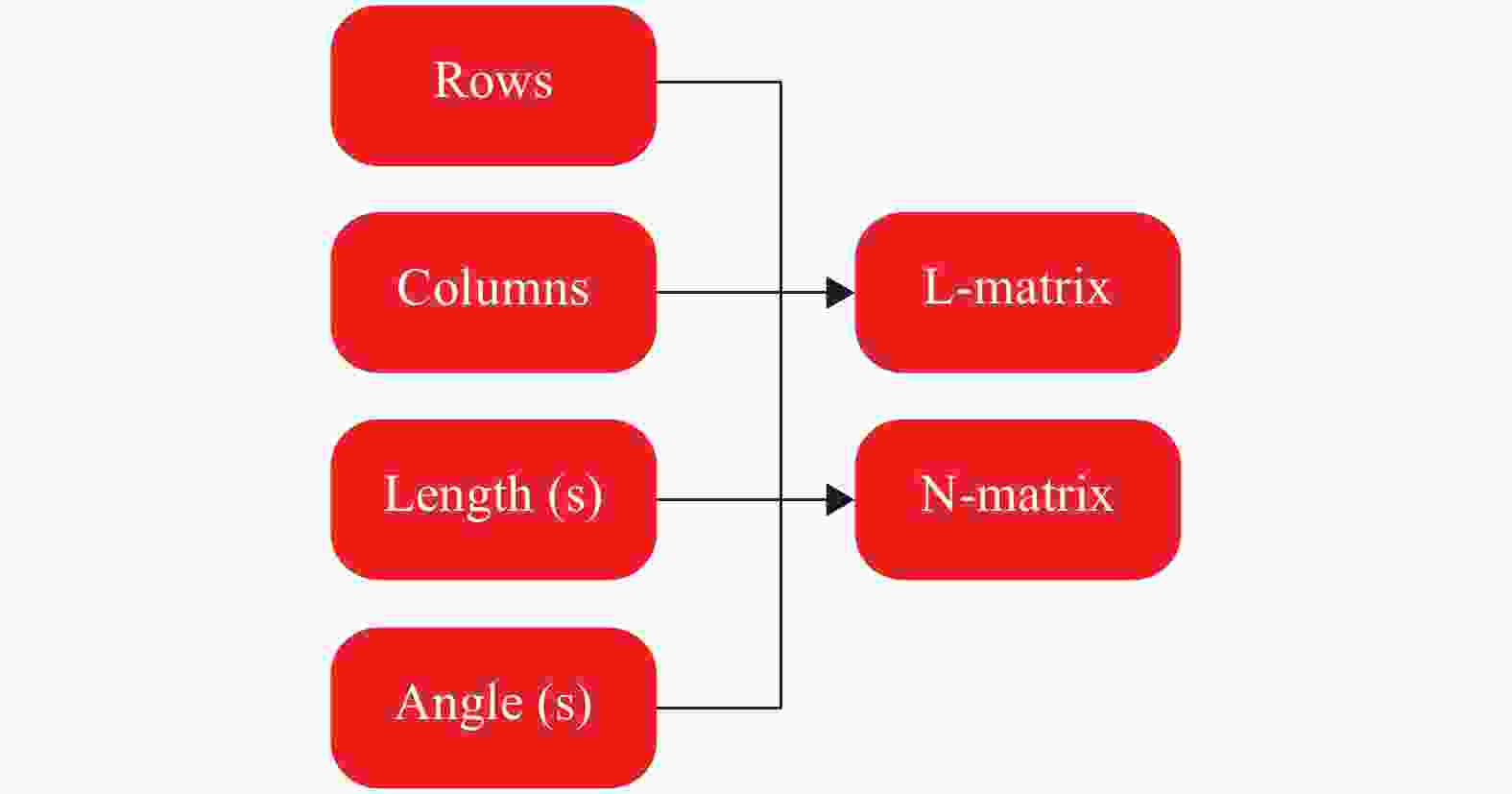
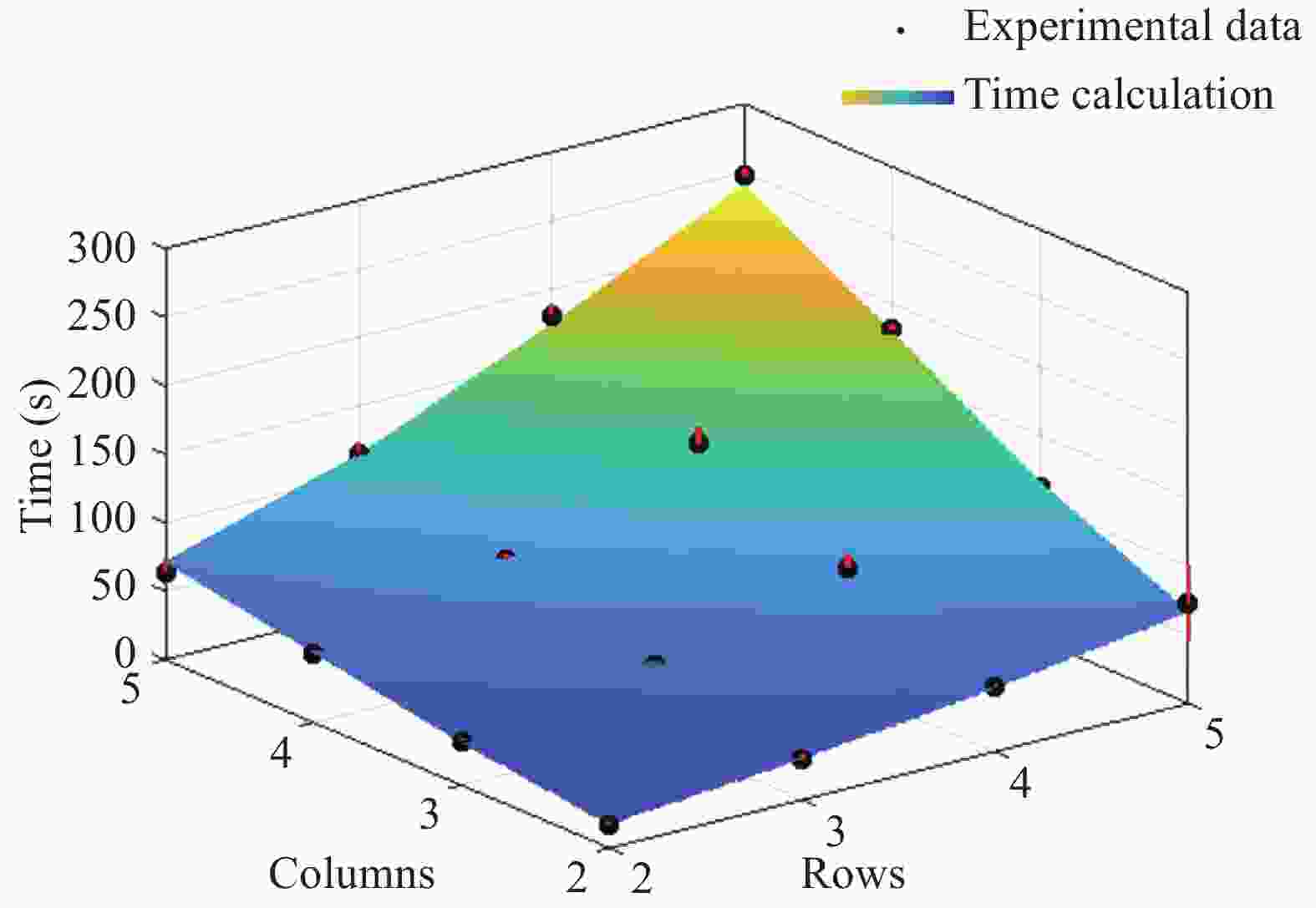
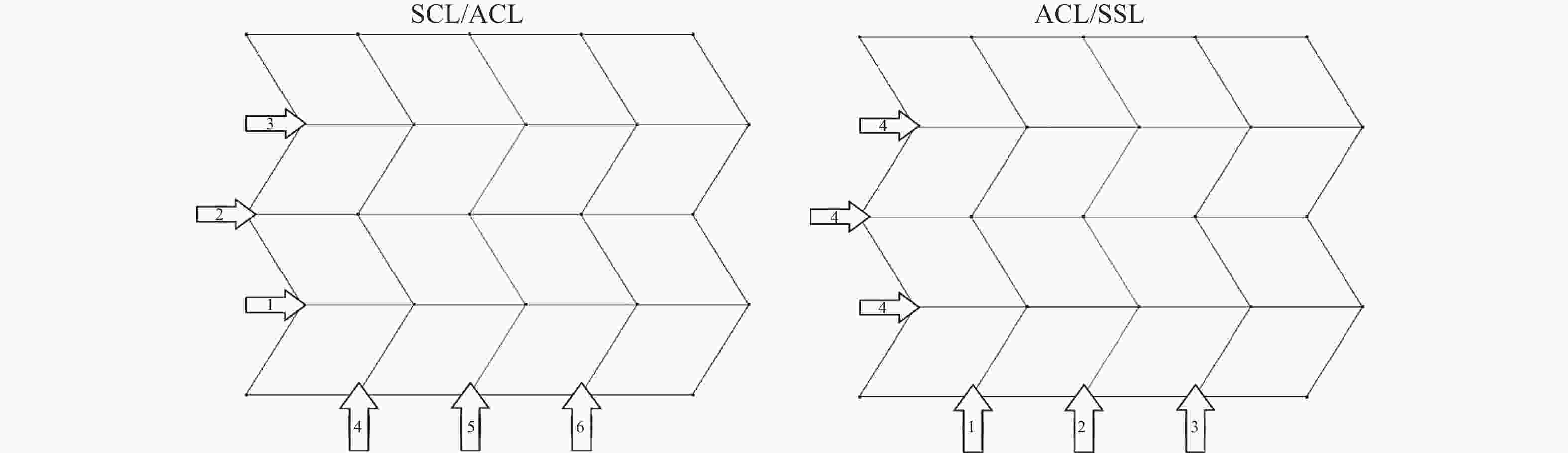
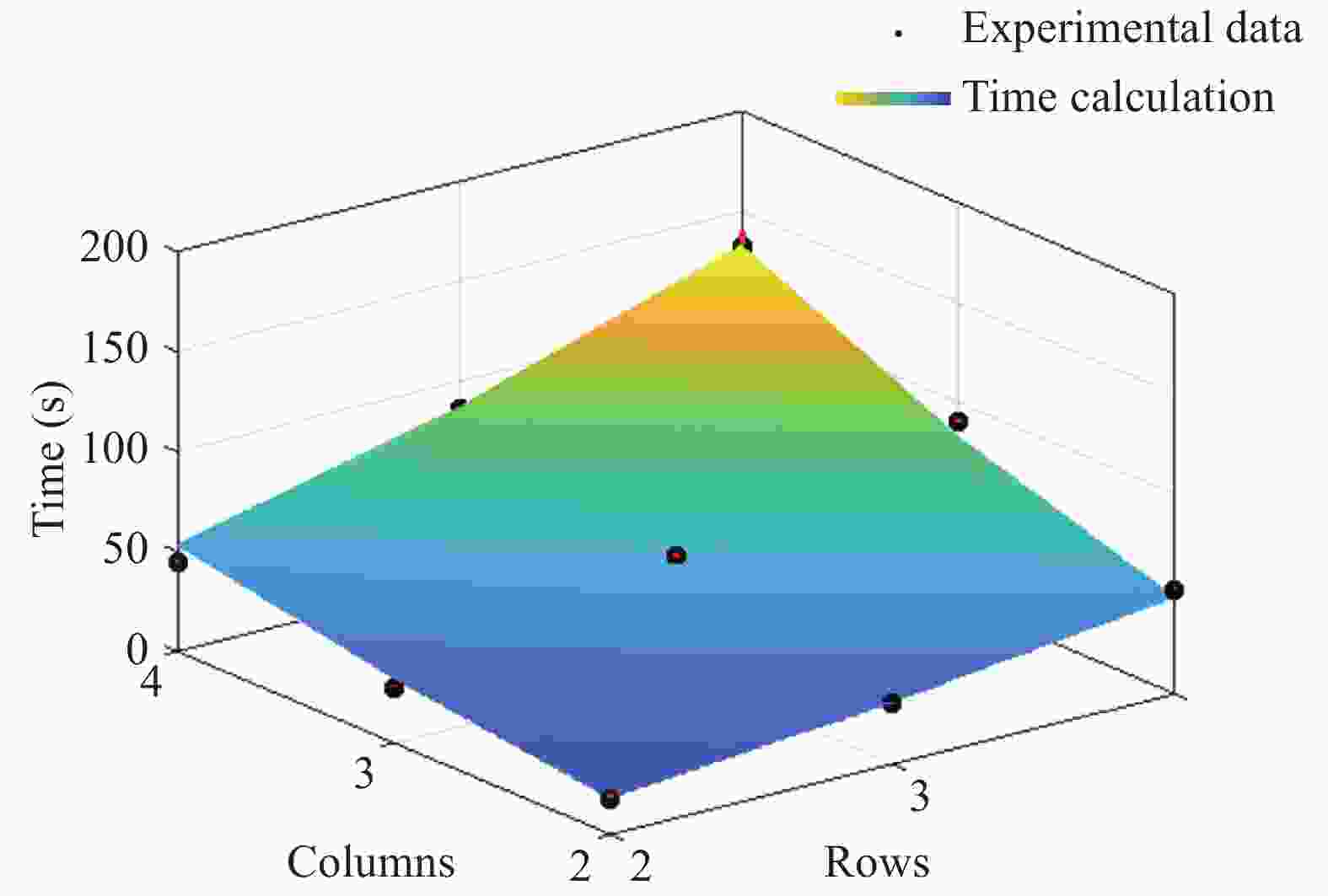
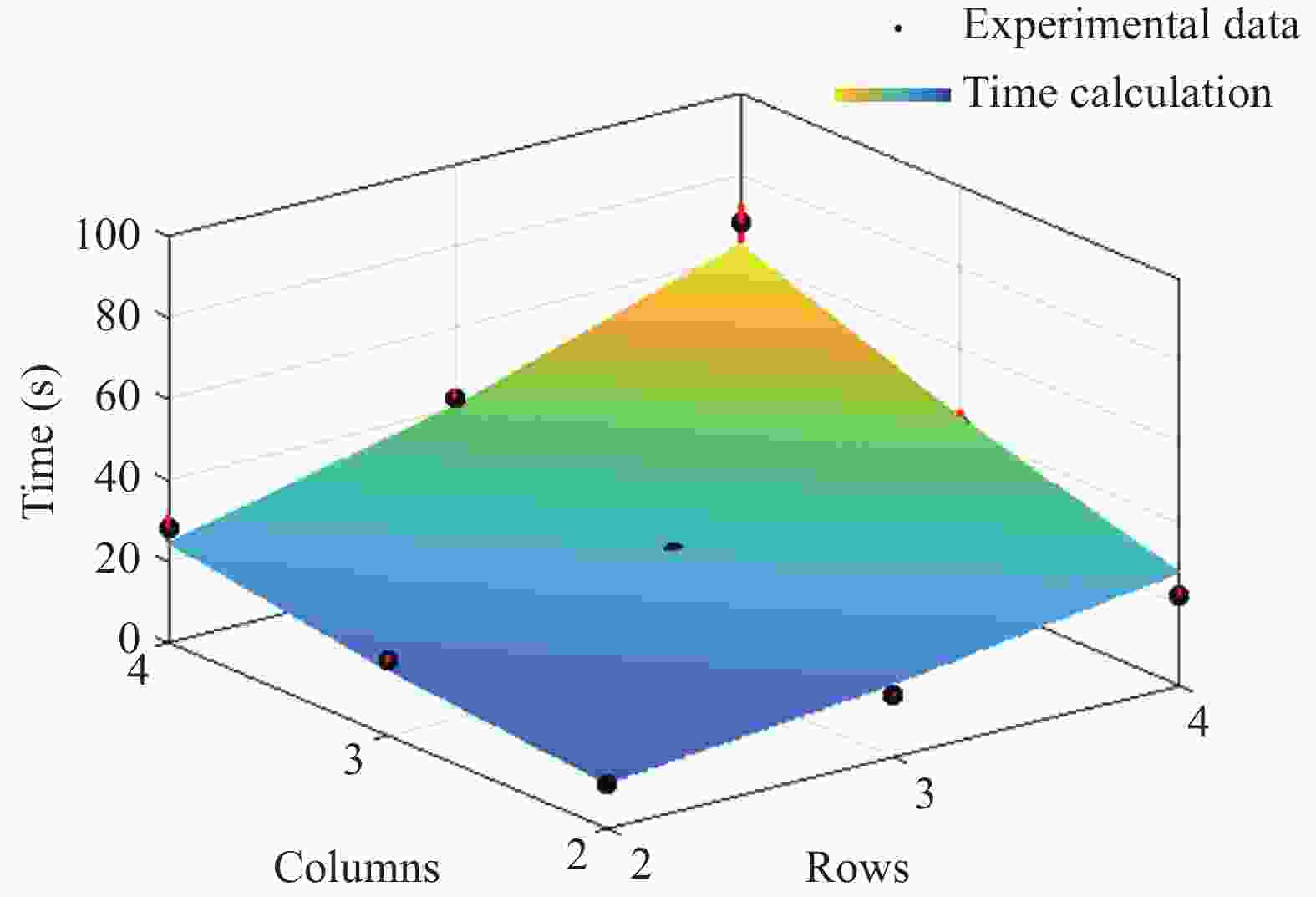
This paper presents a quantitative framework to analyze the complexity of folding origami structures from flat membranes. Extensive efforts have realized intricate origami patterns with desired functions such as mechanical properties, packaging efficiency, and deployment behavior. However, the complexity associated with the manufacturing or folding of origami patterns has not been explored. Understanding how difficult origami structures are to make, and how much time they require to form is crucial information to determining the practical feasibility of origami designs and future applications such as robotic origami assembly in space. In this work, we develop this origami complexity metric by modeling the geometric properties and crease formation of the origami structure, from which it outputs crease and pattern complexity values and a prediction of the time to complete the pattern assembly, based on the characteristics of the operator. The framework is experimentally validated by fabricating various Miura-ori origami paper models.
This paper presents a quantitative framework to analyze the complexity of folding origami structures from flat membranes. Extensive efforts have realized intricate origami patterns with desired functions such as mechanical properties, packaging efficiency, and deployment behavior. However, the complexity associated with the manufacturing or folding of origami patterns has not been explored. Understanding how difficult origami structures are to make, and how much time they require to form is crucial information to determining the practical feasibility of origami designs and future applications such as robotic origami assembly in space. In this work, we develop this origami complexity metric by modeling the geometric properties and crease formation of the origami structure, from which it outputs crease and pattern complexity values and a prediction of the time to complete the pattern assembly, based on the characteristics of the operator. The framework is experimentally validated by fabricating various Miura-ori origami paper models.
Theoretical and Applied Mechanics Letters 11 (2021) 100242.
doi: 10.1016/j.taml.2021.100242
Abstract:
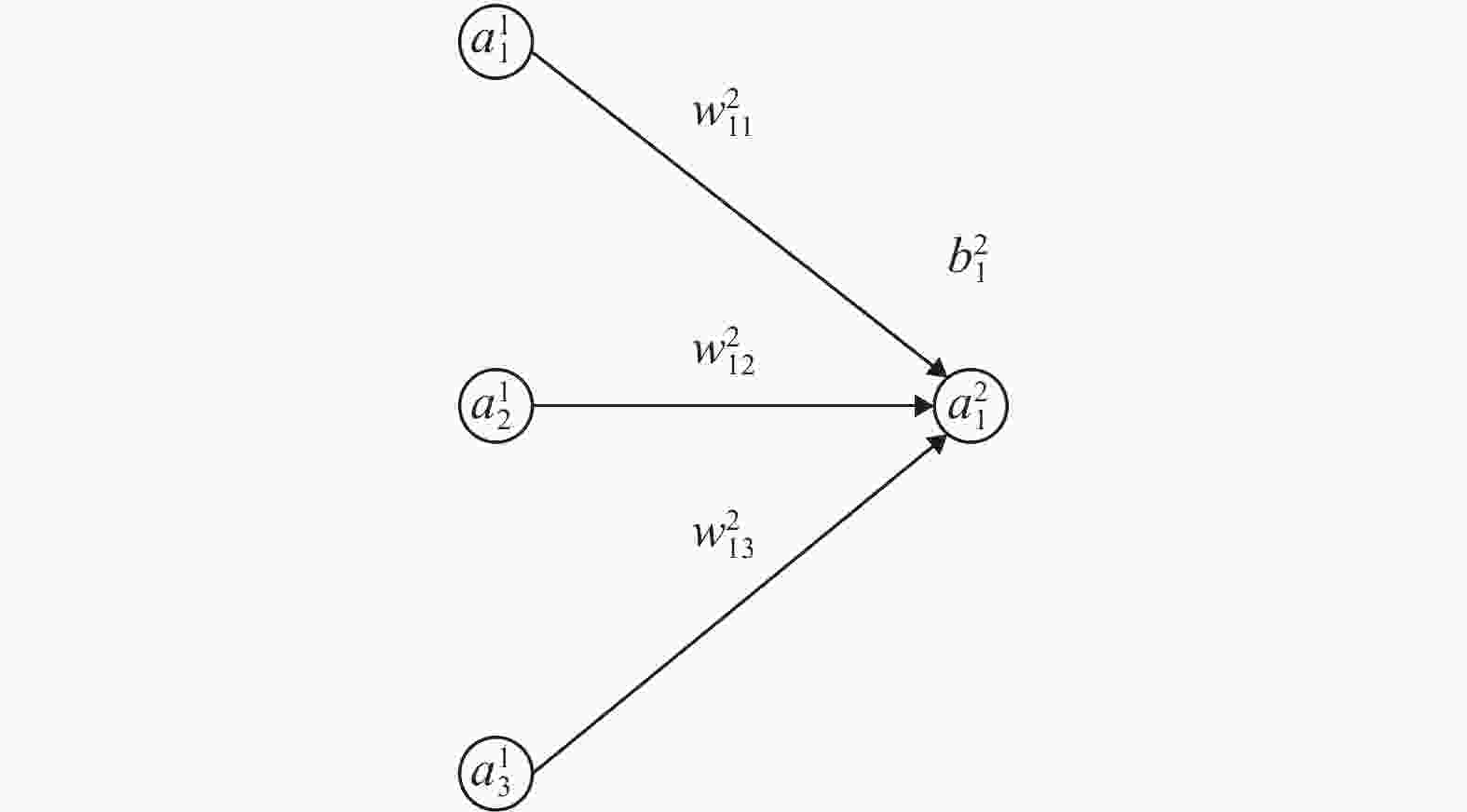
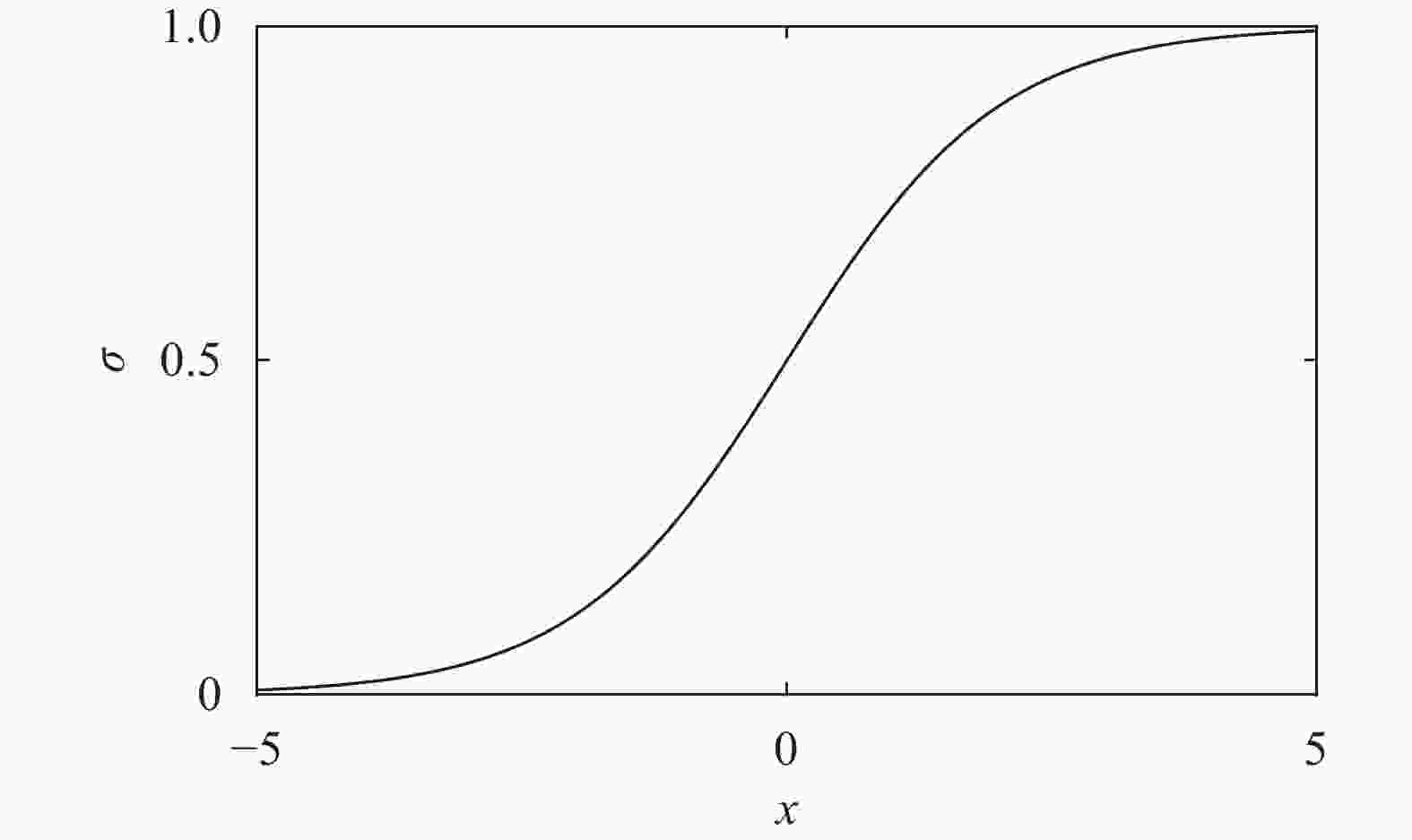
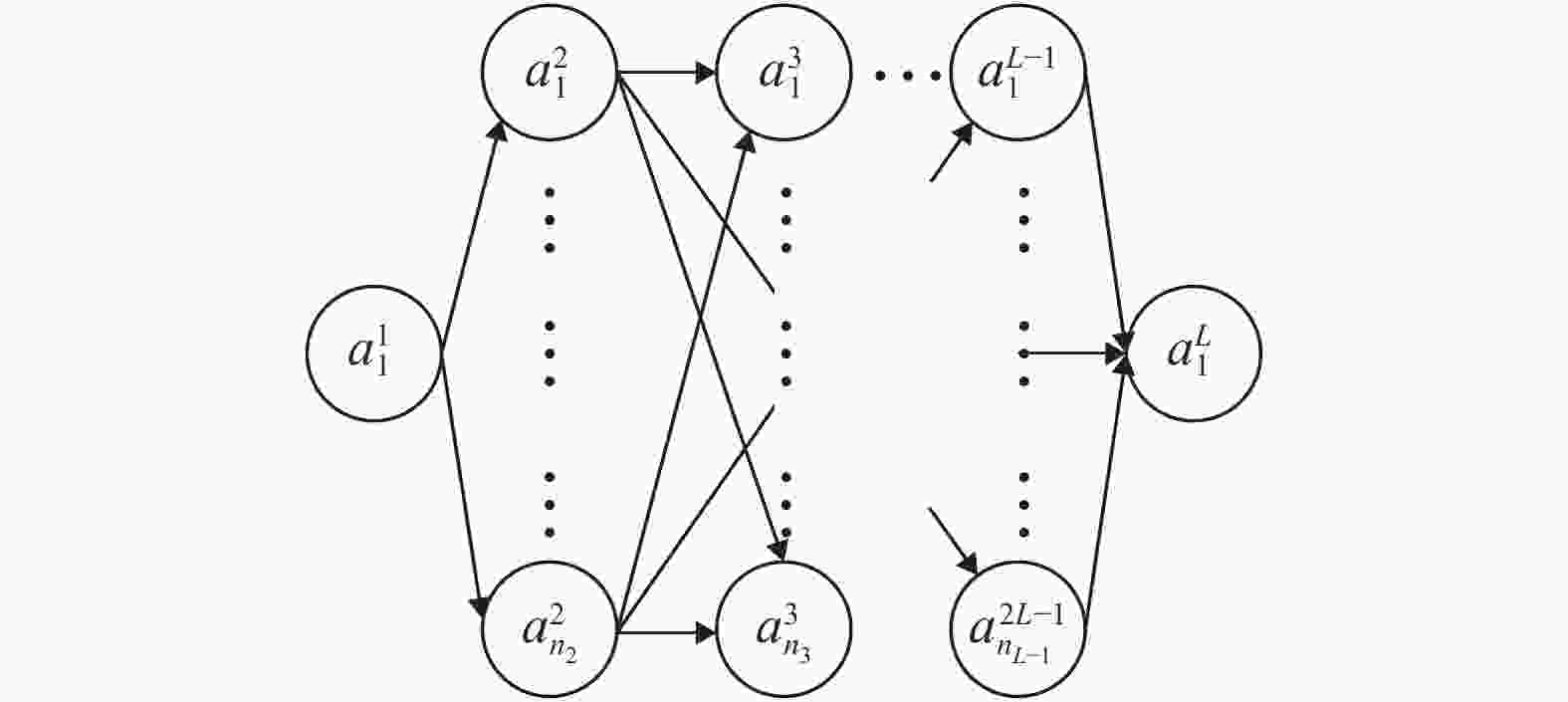
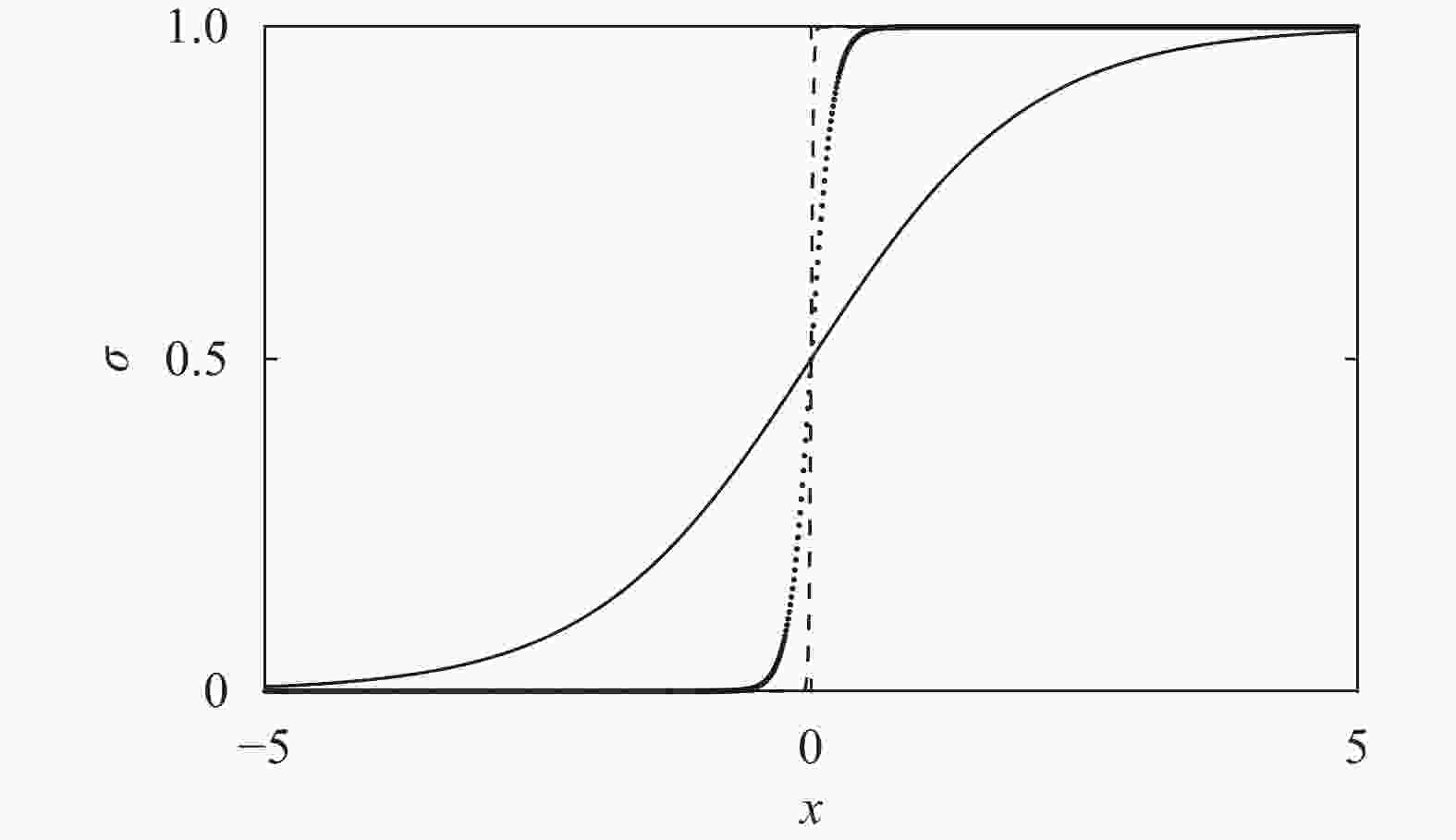
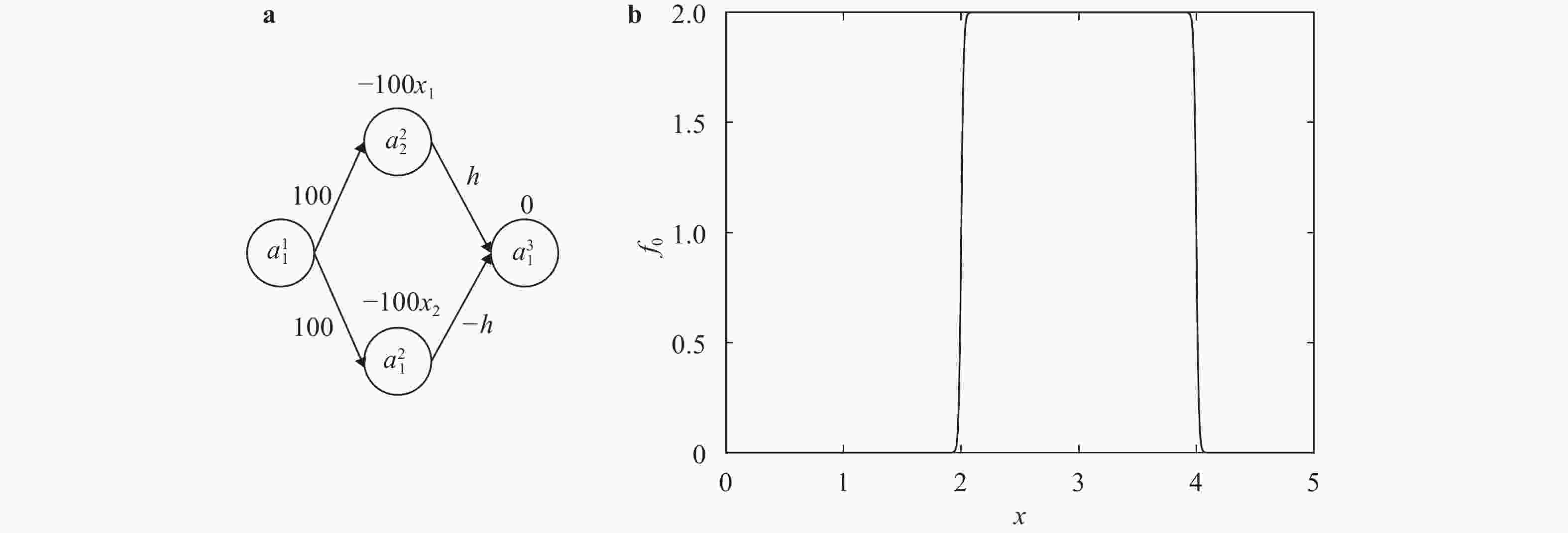
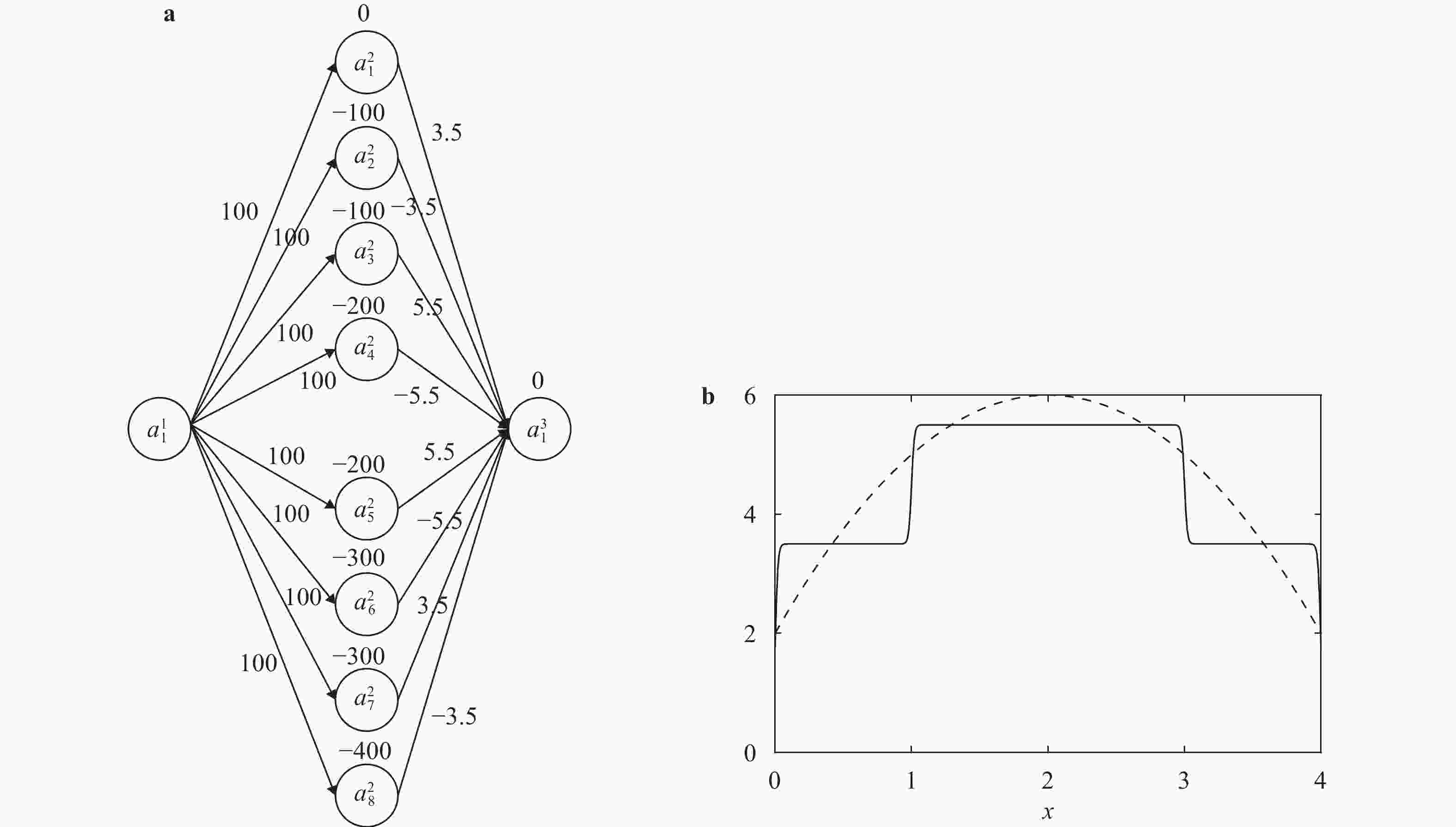
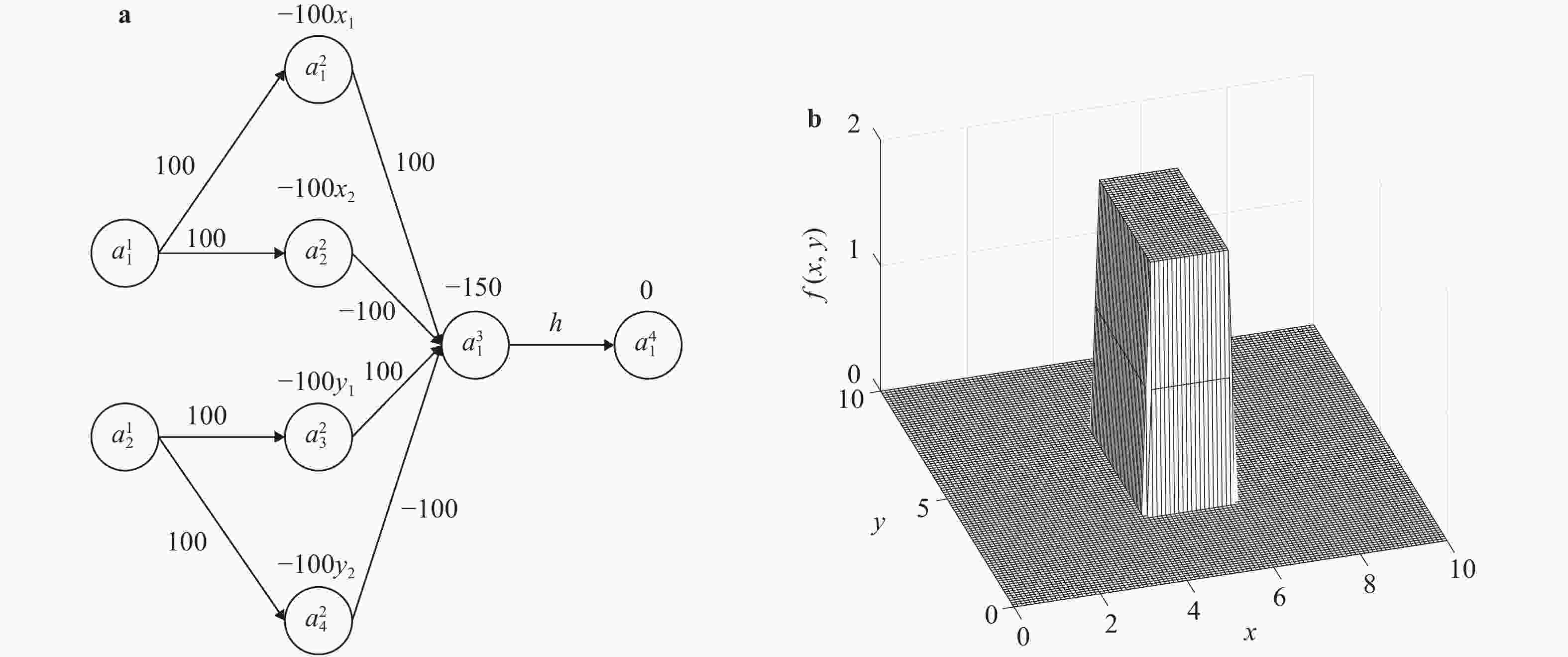
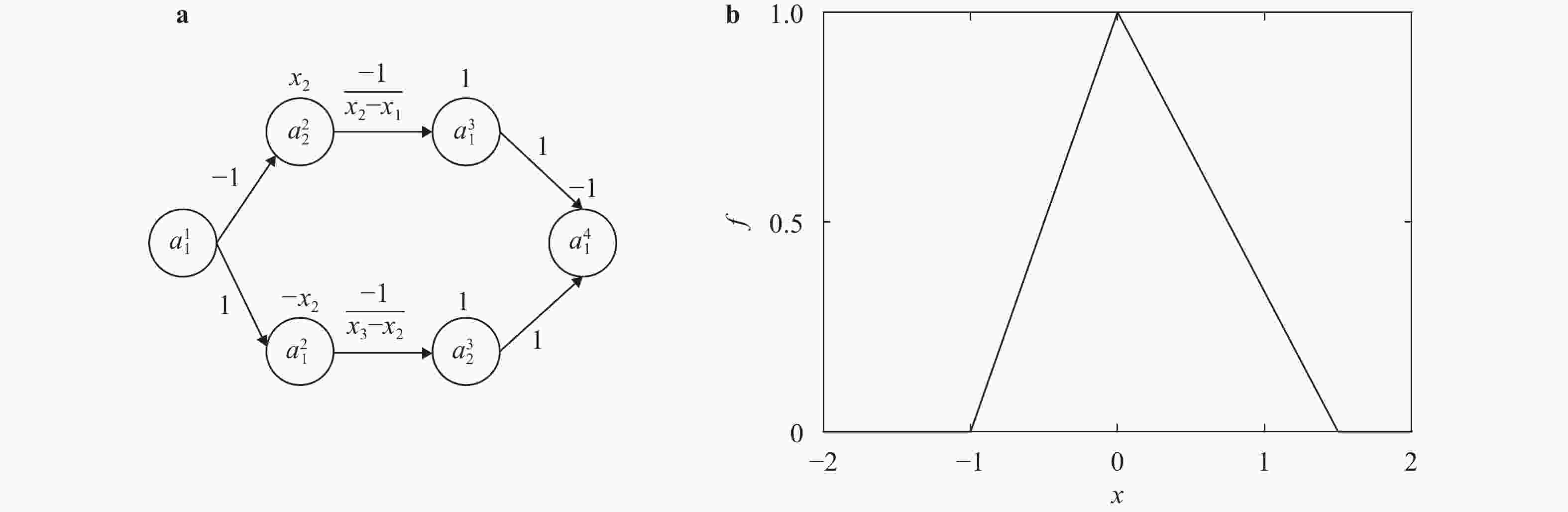
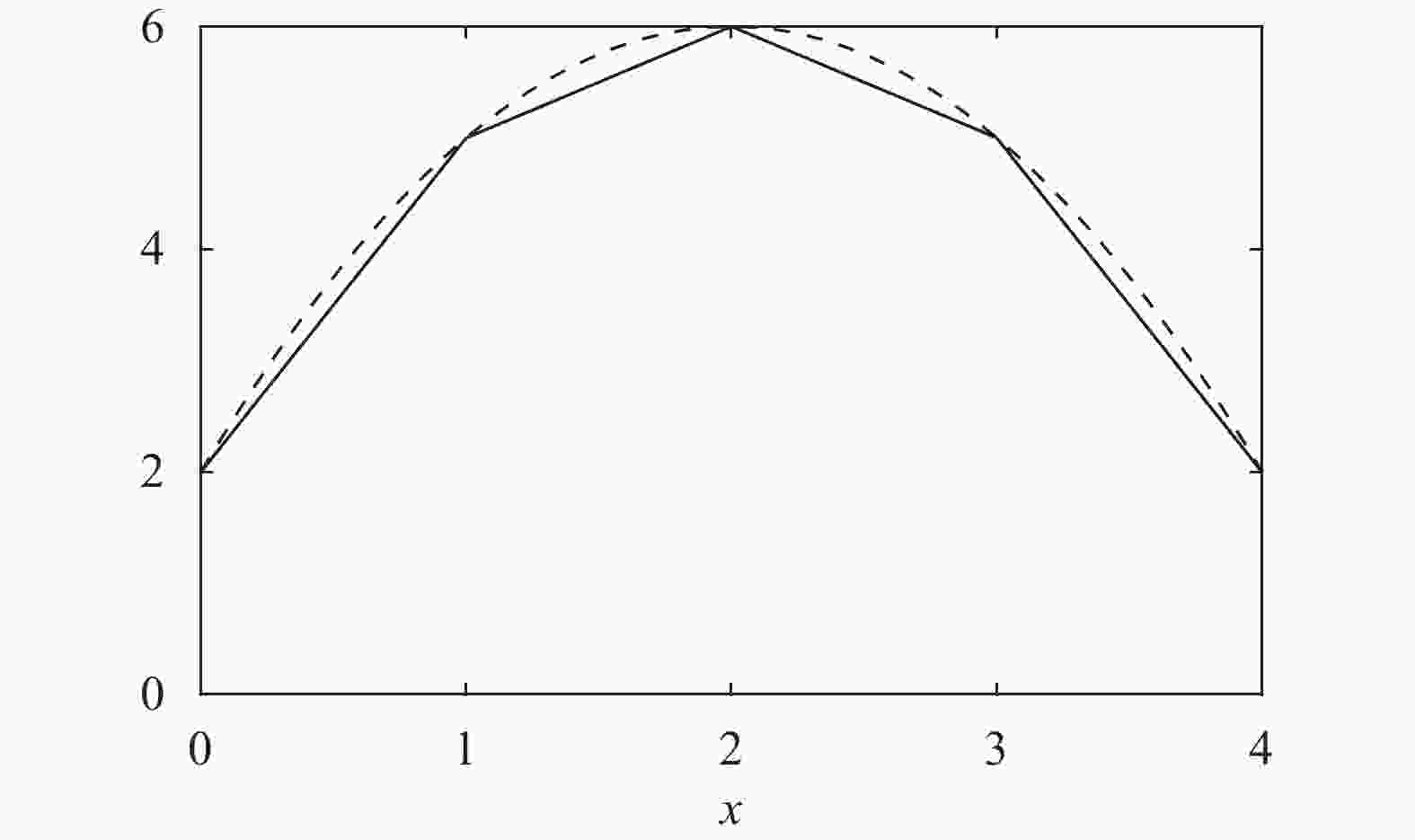
In recent years, neural networks have become an increasingly powerful tool in scientific computing. The universal approximation theorem asserts that a neural network may be constructed to approximate any given continuous function at desired accuracy. The backpropagation algorithm further allows efficient optimization of the parameters in training a neural network. Powered by GPU's, effective computations for scientific and engineering problems are thereby enabled. In addition, we show that finite element shape functions may also be approximated by neural networks.
In recent years, neural networks have become an increasingly powerful tool in scientific computing. The universal approximation theorem asserts that a neural network may be constructed to approximate any given continuous function at desired accuracy. The backpropagation algorithm further allows efficient optimization of the parameters in training a neural network. Powered by GPU's, effective computations for scientific and engineering problems are thereby enabled. In addition, we show that finite element shape functions may also be approximated by neural networks.
Theoretical and Applied Mechanics Letters 11 (2021) 100243.
doi: 10.1016/j.taml.2021.100243
Abstract:
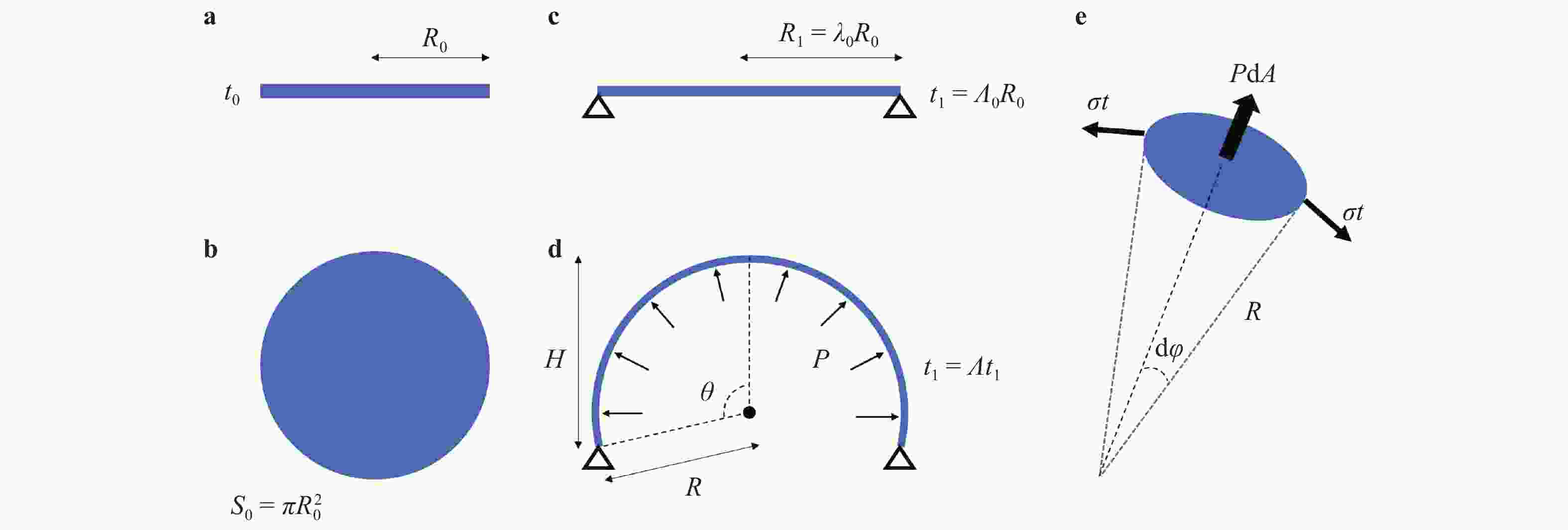
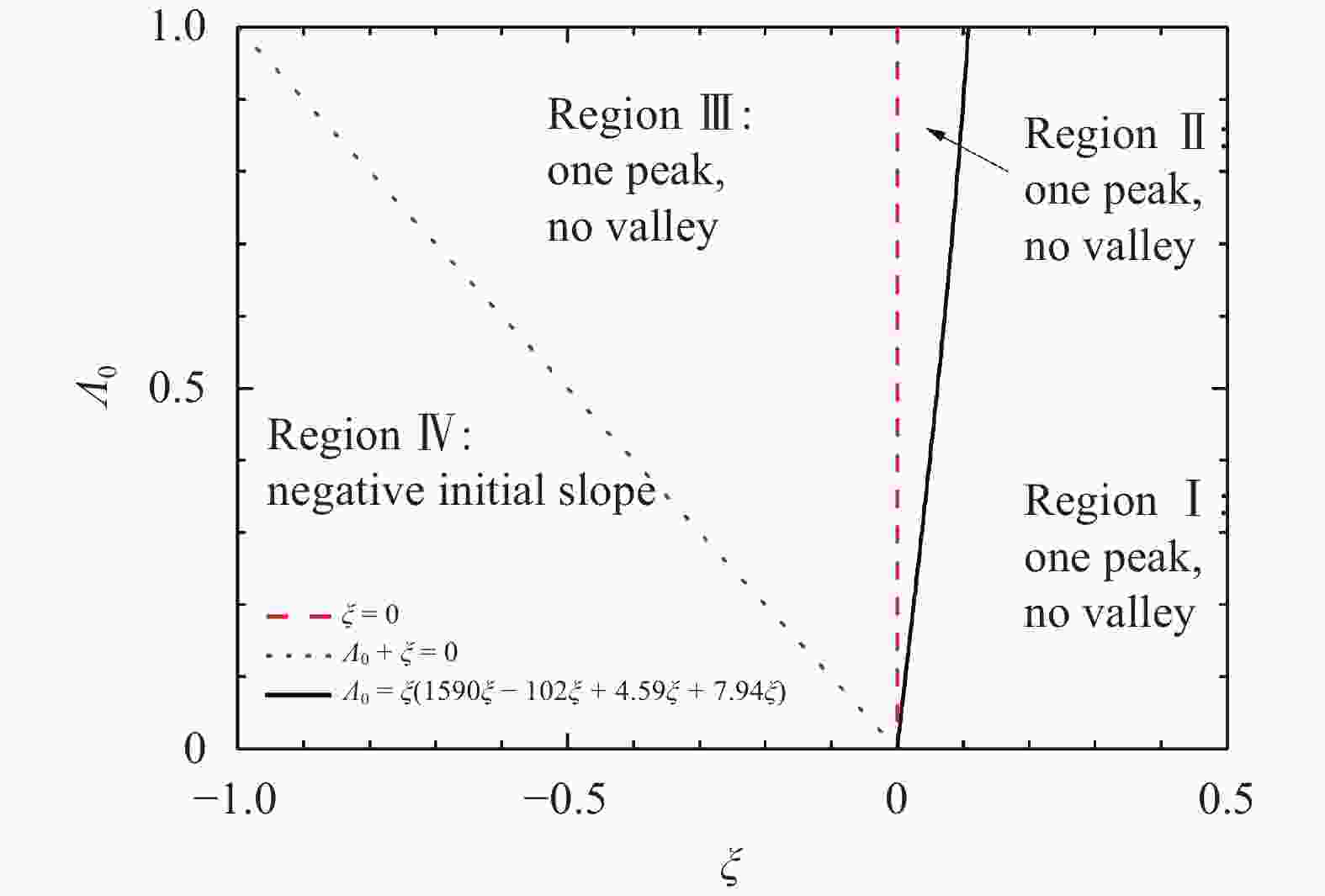
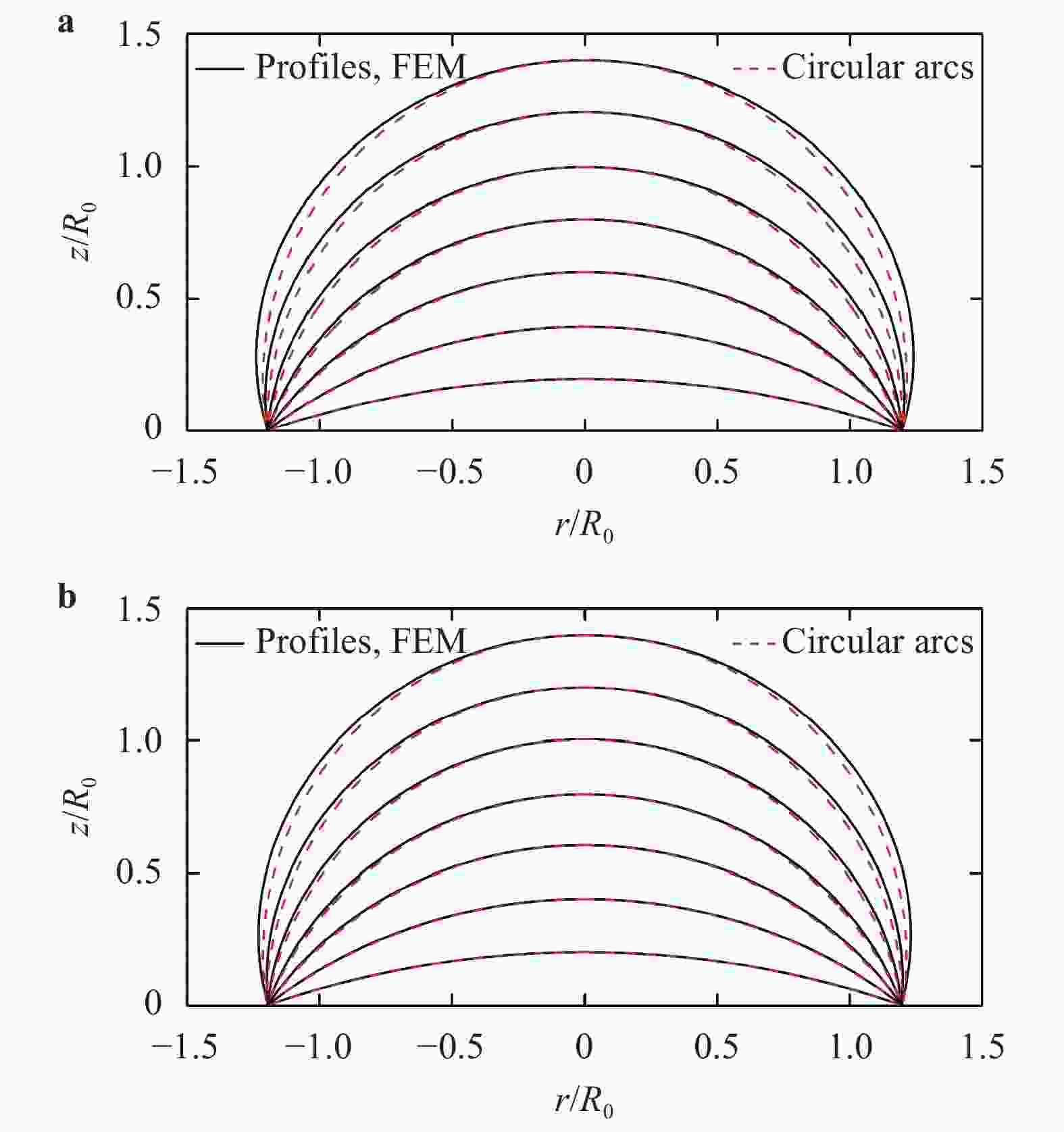
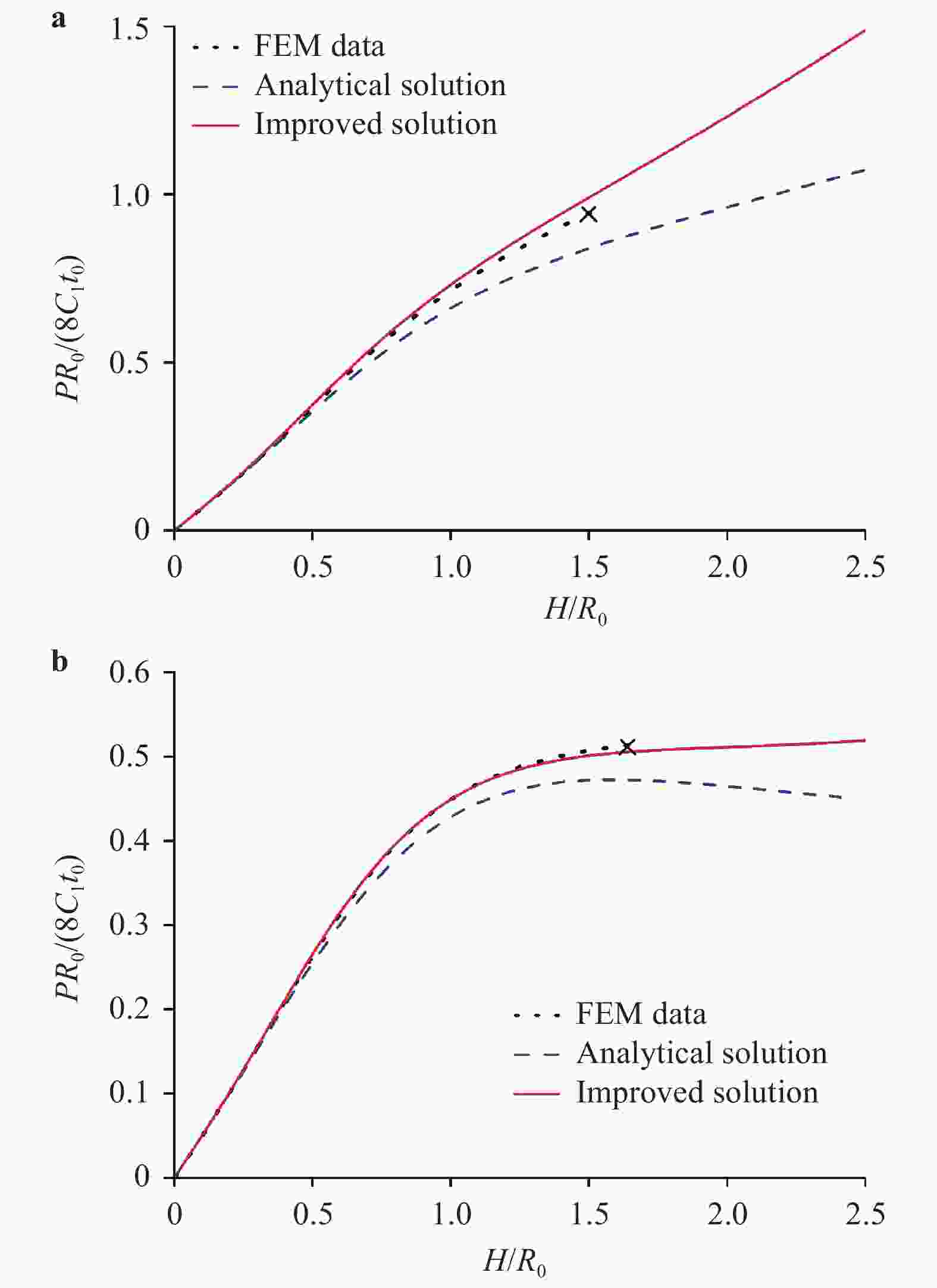
Elastomeric membranes are frequently used in several emerging fields such as soft robotics and flexible electronics. For convenience of the structural design, it is very attractive to find simple analytical solutions to well describe their elastic deformations in response to external loadings. However, both the material/geometrical nonlinearity and the deformation inhomogeneity due to boundary constraints make it much challenging to get an exact analytical solution. In this paper, we focus on the inflation of a pre-stretched elastomeric circular membrane under uniform pressure, and derive an approximate analytical solution of the pressure-volume curve based upon a reasonable assumption on the shape of the inflated membrane. Such an explicit expression enables us to quantitatively design the material and geometrical parameters of the pre-stretched membrane to generate a target pressure-volume curve with prescribed peak point and initial slope. This work would be of help in the simplified mechanical design of structures involving elastomeric membranes.
Elastomeric membranes are frequently used in several emerging fields such as soft robotics and flexible electronics. For convenience of the structural design, it is very attractive to find simple analytical solutions to well describe their elastic deformations in response to external loadings. However, both the material/geometrical nonlinearity and the deformation inhomogeneity due to boundary constraints make it much challenging to get an exact analytical solution. In this paper, we focus on the inflation of a pre-stretched elastomeric circular membrane under uniform pressure, and derive an approximate analytical solution of the pressure-volume curve based upon a reasonable assumption on the shape of the inflated membrane. Such an explicit expression enables us to quantitatively design the material and geometrical parameters of the pre-stretched membrane to generate a target pressure-volume curve with prescribed peak point and initial slope. This work would be of help in the simplified mechanical design of structures involving elastomeric membranes.
Theoretical and Applied Mechanics Letters 11 (2021) 100244.
doi: 10.1016/j.taml.2021.100244
Abstract:
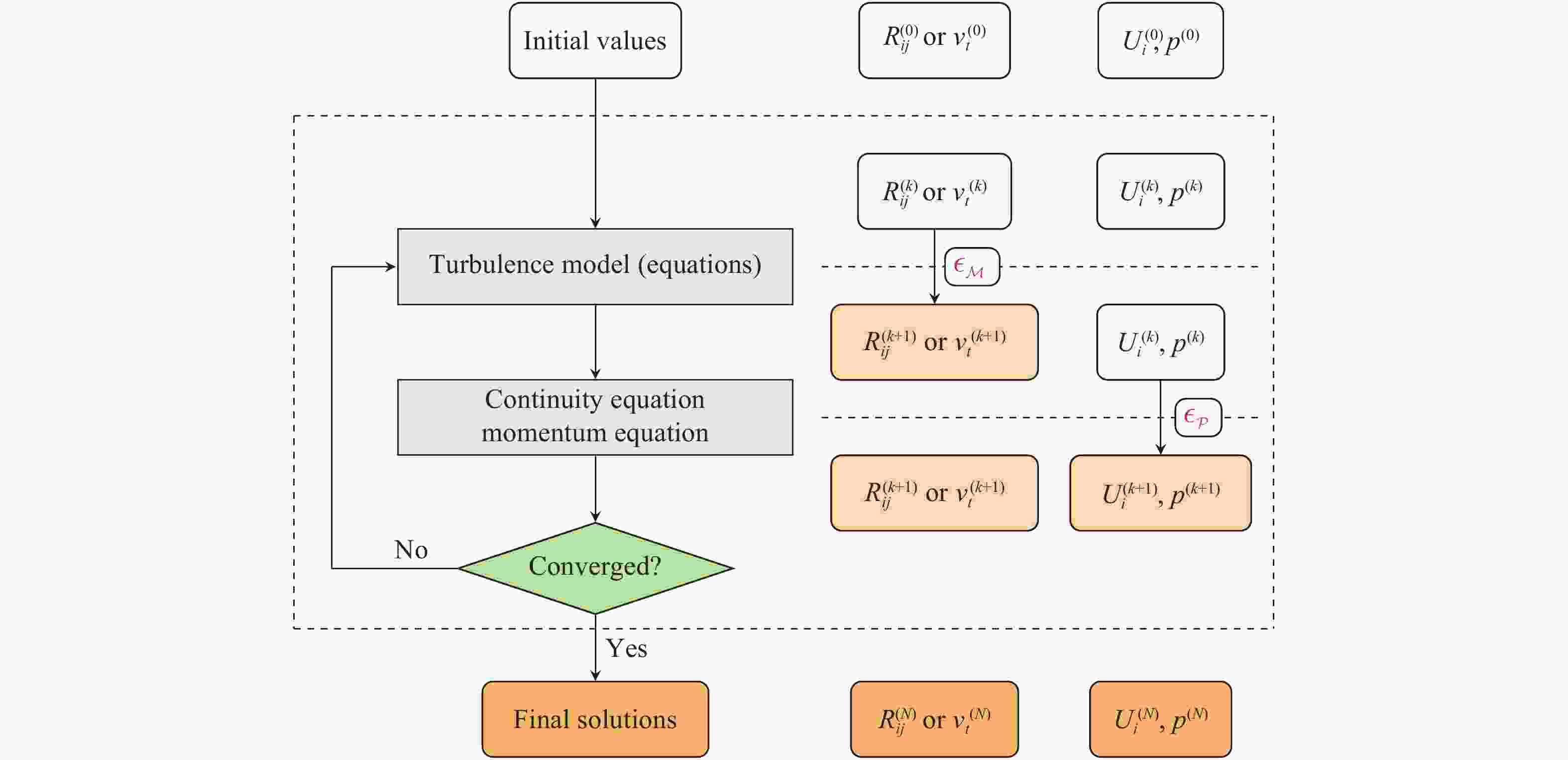
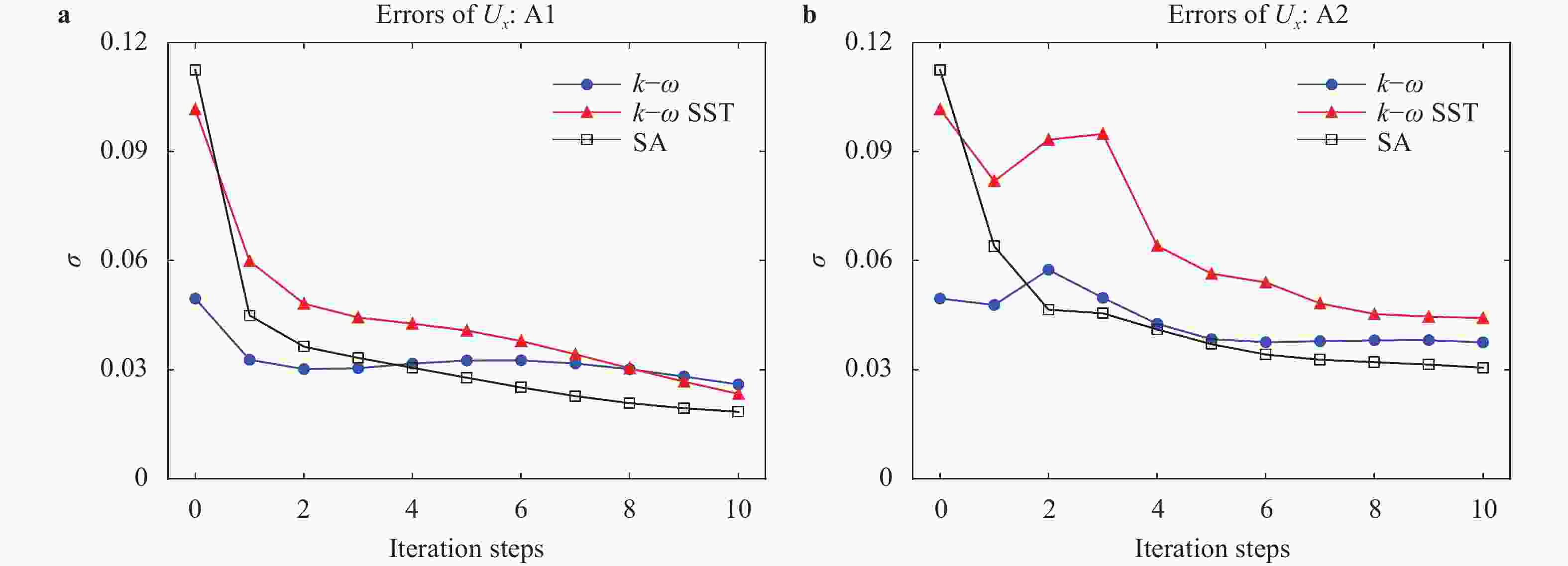
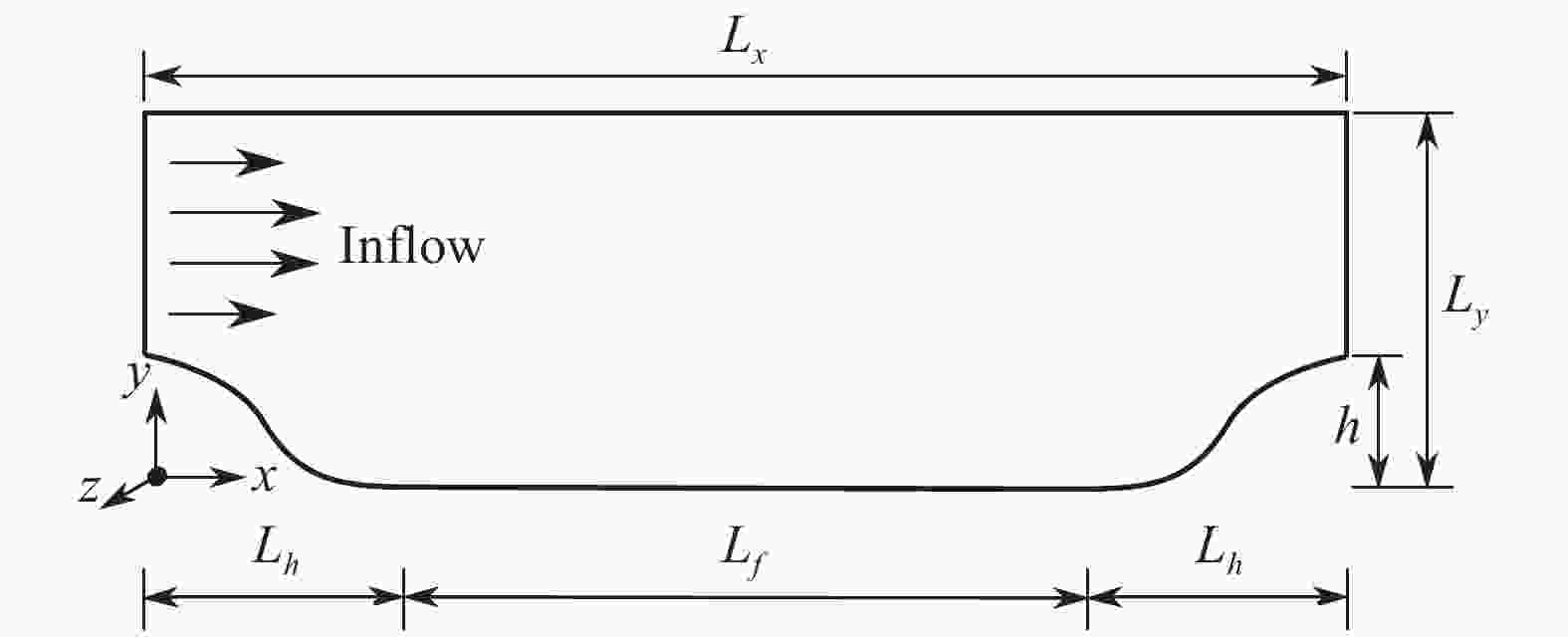
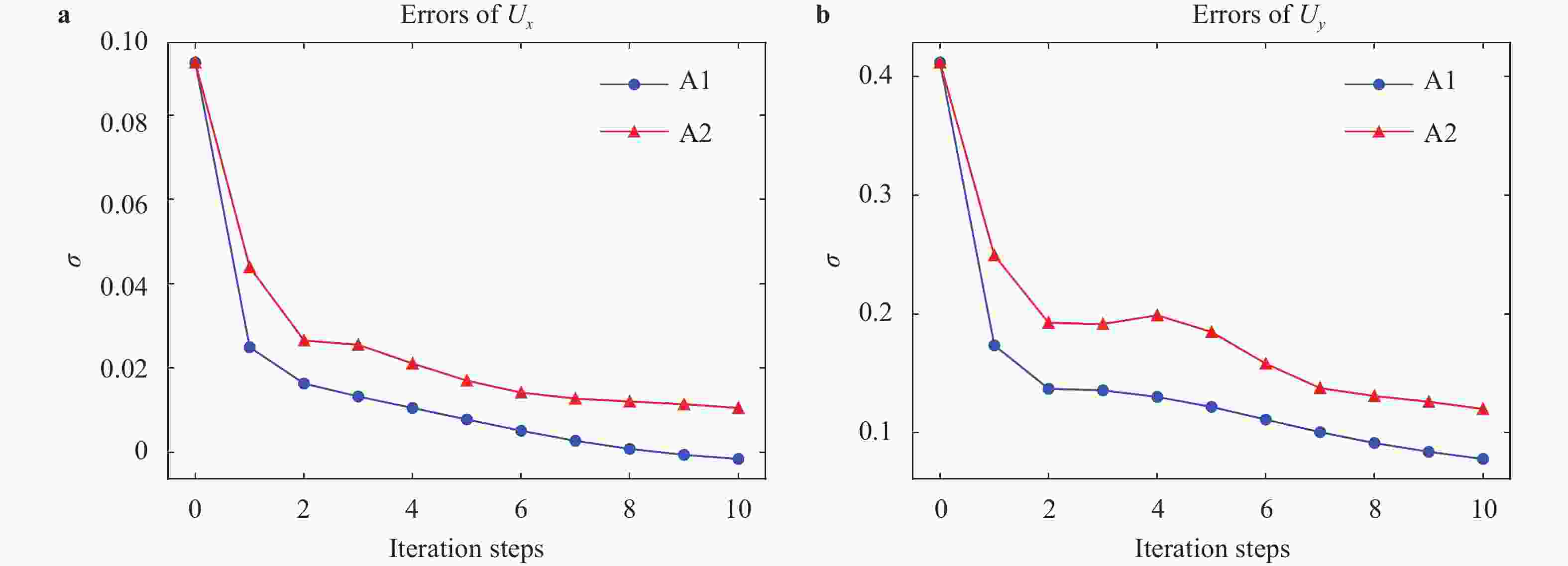
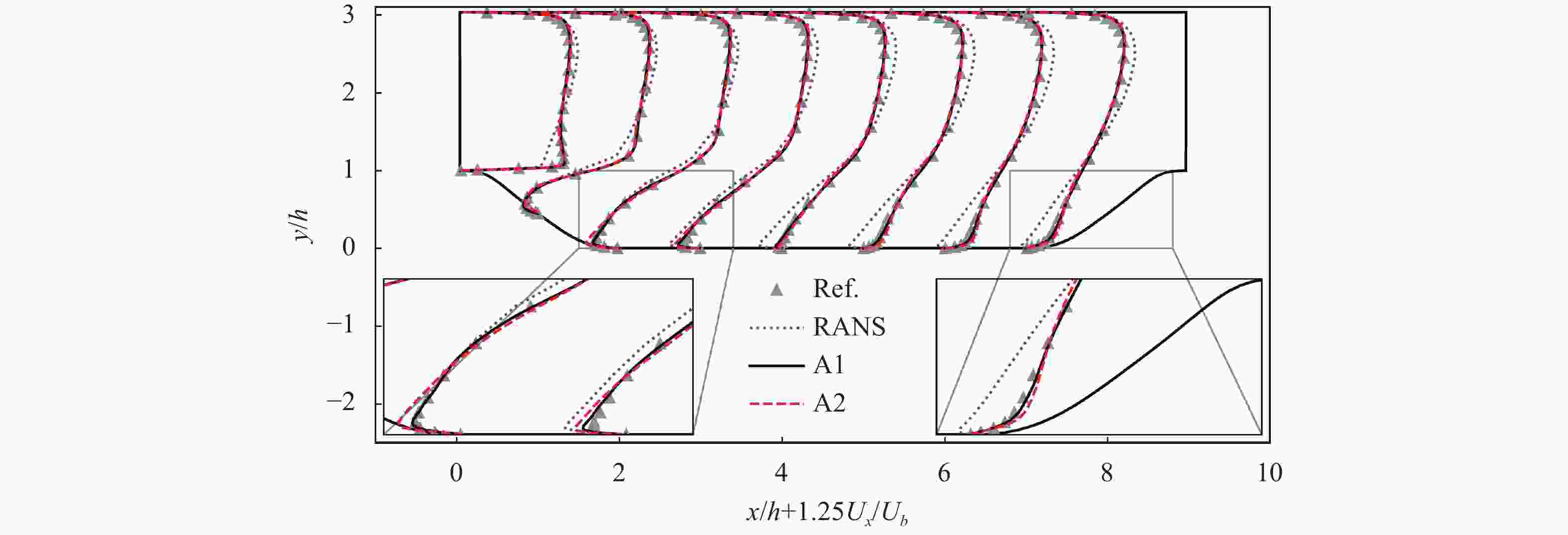
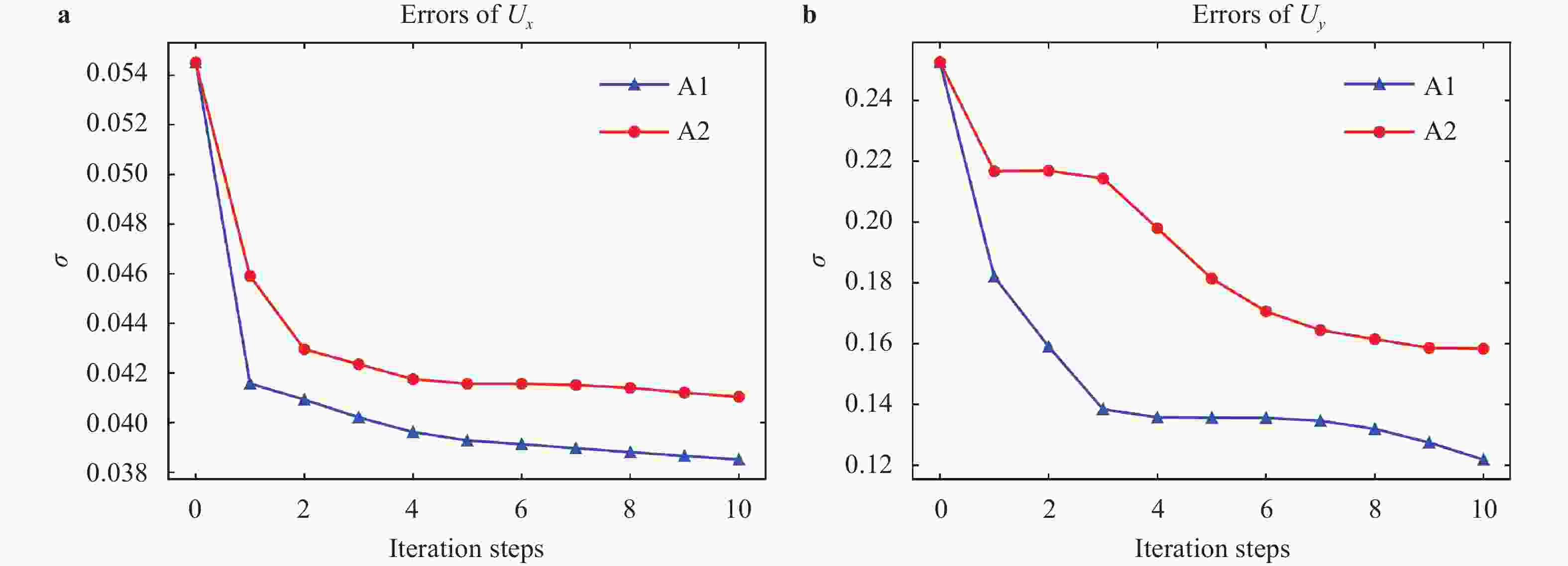
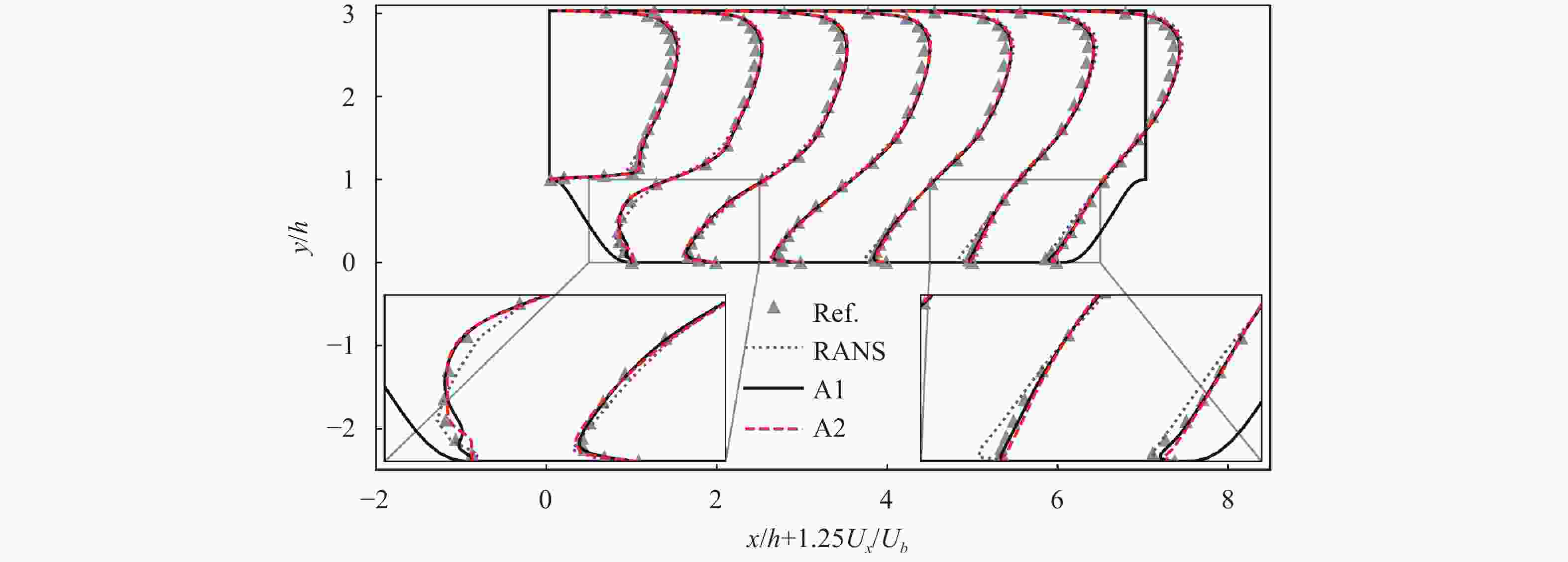
With the rising of modern data science, data-driven turbulence modeling with the aid of machine learning algorithms is becoming a new promising field. Many approaches are able to achieve better Reynolds stress prediction, with much lower modeling error (\begin{document}$\epsilon_{\rm{M}}$\end{document} ![]()
![]()
\begin{document}$\epsilon_{\rm{P}}$\end{document} ![]()
![]()
\begin{document}$\epsilon_{\rm{P}}$\end{document} ![]()
![]()
\begin{document}$\epsilon_{\rm{M}}$\end{document} ![]()
![]()
\begin{document}$\epsilon_{\rm{P}}$\end{document} ![]()
![]()
\begin{document}$\nu_{\rm{t}}^*$\end{document} ![]()
![]()
\begin{document}$S_{ij}^0$\end{document} ![]()
![]()
\begin{document}$\epsilon_{\rm{P}}$\end{document} ![]()
![]()
With the rising of modern data science, data-driven turbulence modeling with the aid of machine learning algorithms is becoming a new promising field. Many approaches are able to achieve better Reynolds stress prediction, with much lower modeling error (
Theoretical and Applied Mechanics Letters 11 (2021) 100245.
doi: 10.1016/j.taml.2021.100245
Abstract:
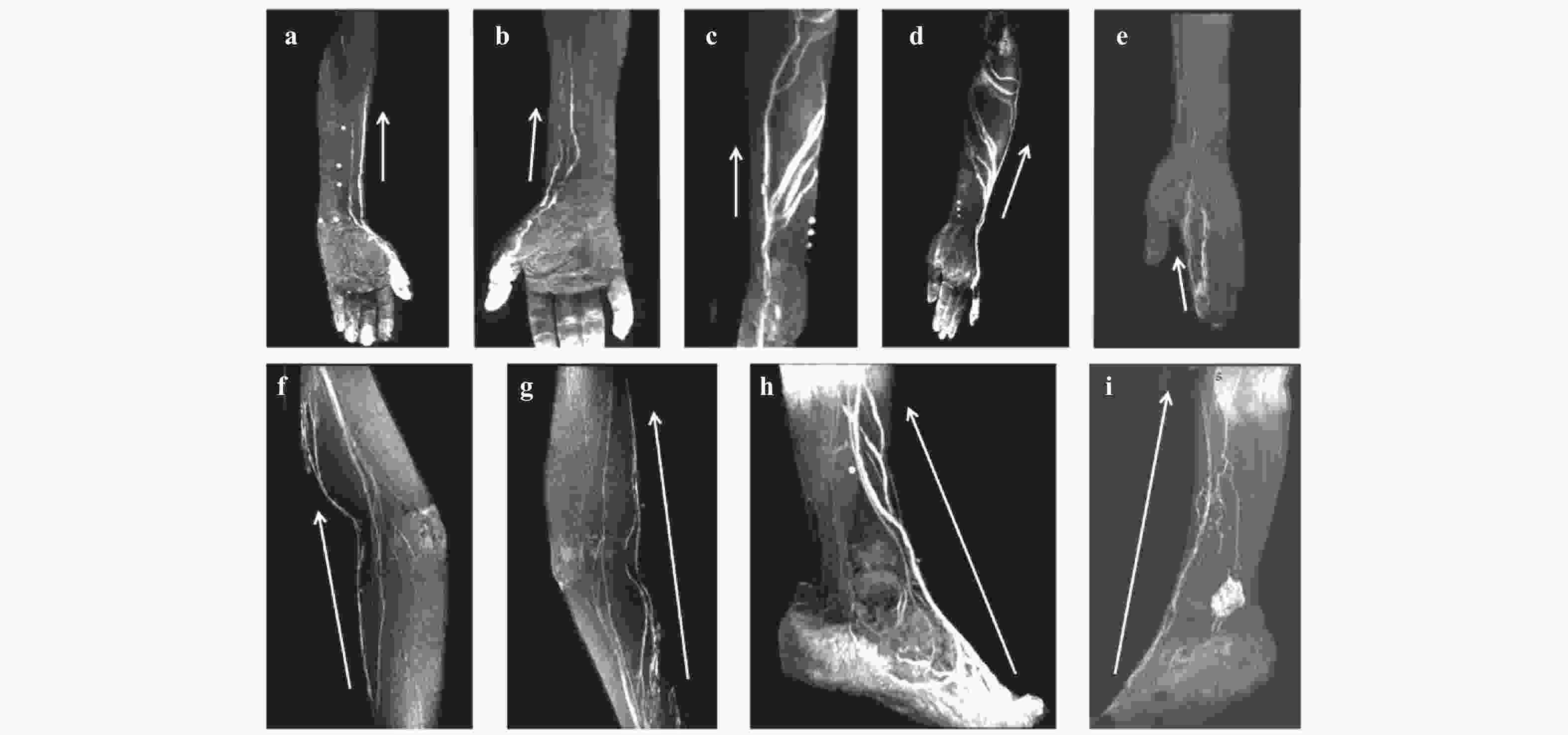
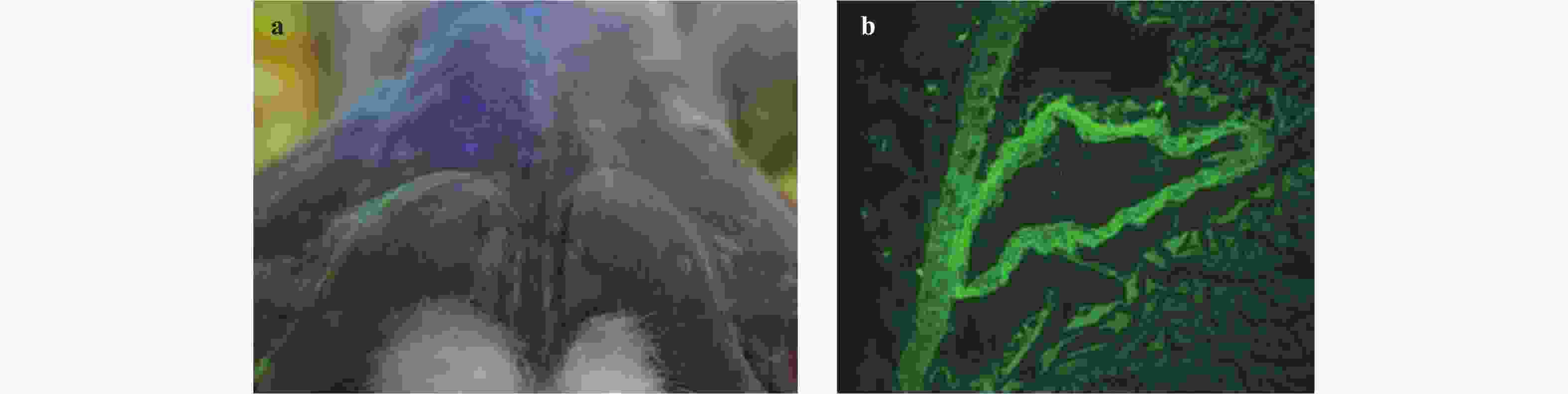
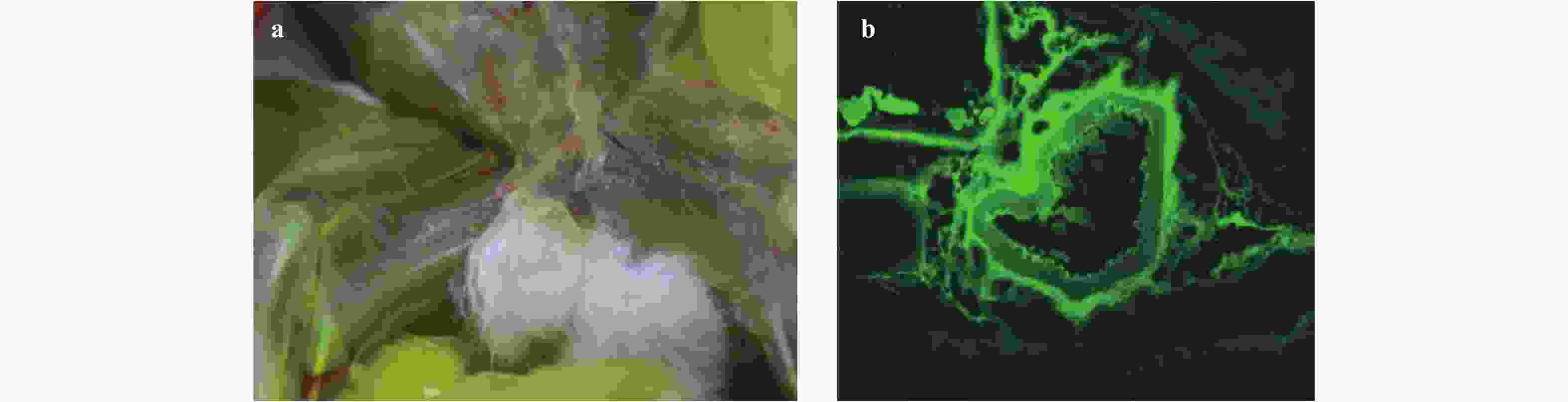
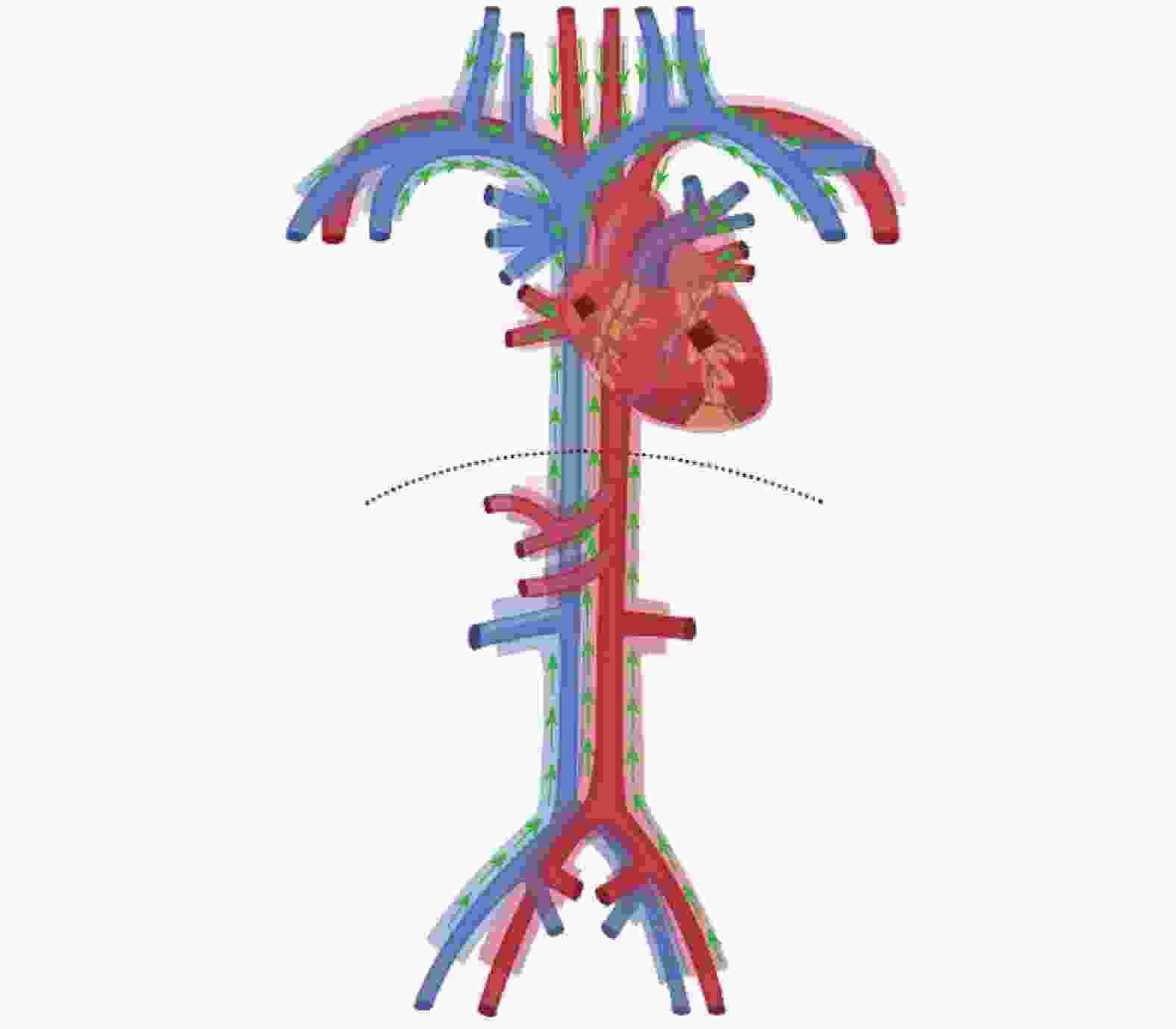
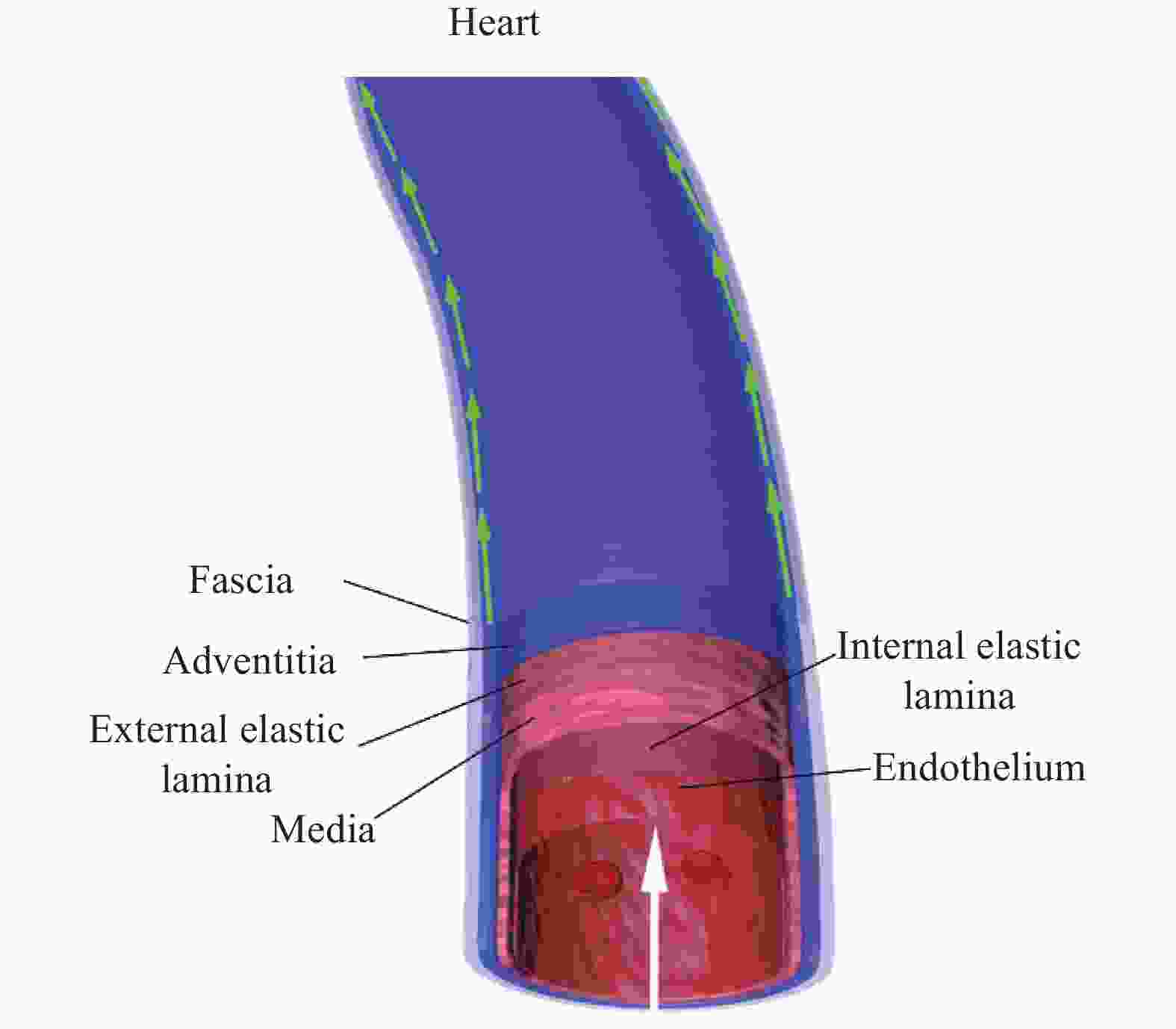
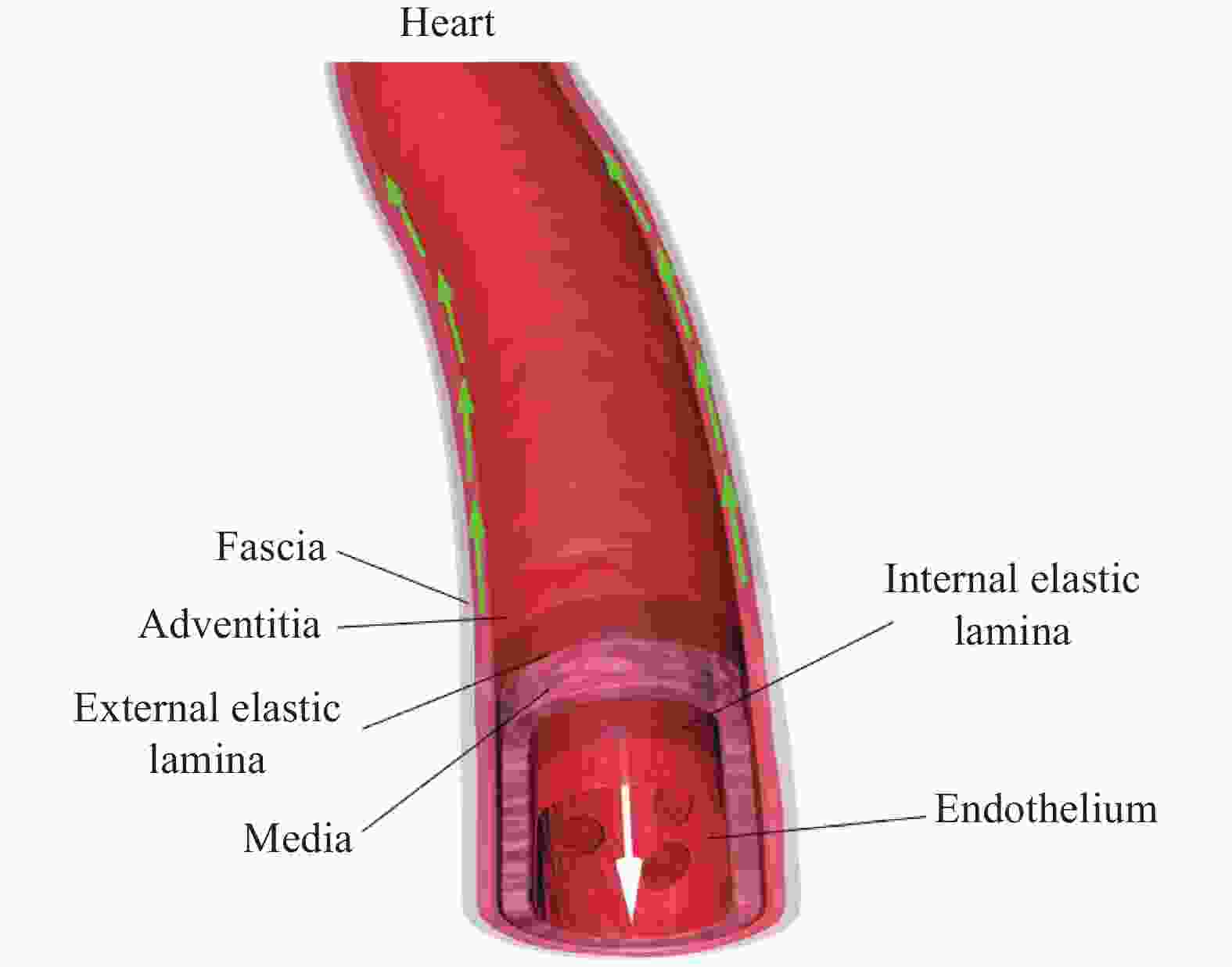
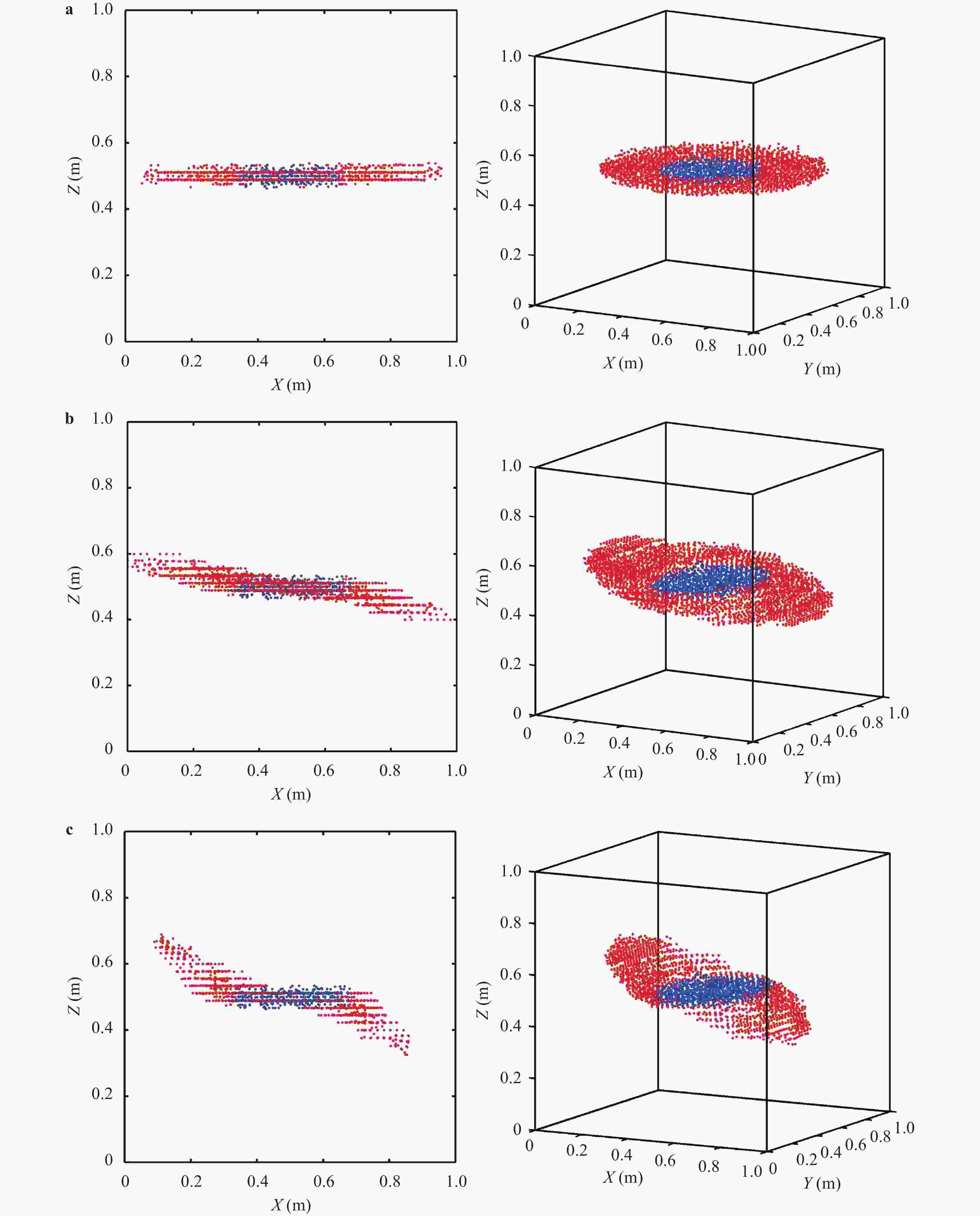
In the previous studies, the phenomenon that the interstitial fluid (ISF) can flow along tunica adventitia of the arteries and veins in both human and animal bodies was reported. On the basis of these studies, this paper aims to: (i) summarize the basic properties of the ISF flows in the walls of arteries and veins, (ii) combine the basic properties with axiomaticism and abstract the axiom for ISF flows, and (iii) propose three fundamental laws of the ISF flow, (i.e., the existence law, the homotropic law and the reverse law). The three laws provide solid theoretical basement for exploring the kinematic patterns of interstitial fluid flow in the cardiovascular system.
In the previous studies, the phenomenon that the interstitial fluid (ISF) can flow along tunica adventitia of the arteries and veins in both human and animal bodies was reported. On the basis of these studies, this paper aims to: (i) summarize the basic properties of the ISF flows in the walls of arteries and veins, (ii) combine the basic properties with axiomaticism and abstract the axiom for ISF flows, and (iii) propose three fundamental laws of the ISF flow, (i.e., the existence law, the homotropic law and the reverse law). The three laws provide solid theoretical basement for exploring the kinematic patterns of interstitial fluid flow in the cardiovascular system.
Theoretical and Applied Mechanics Letters 11 (2021) 100246.
doi: 10.1016/j.taml.2021.100246
Abstract:
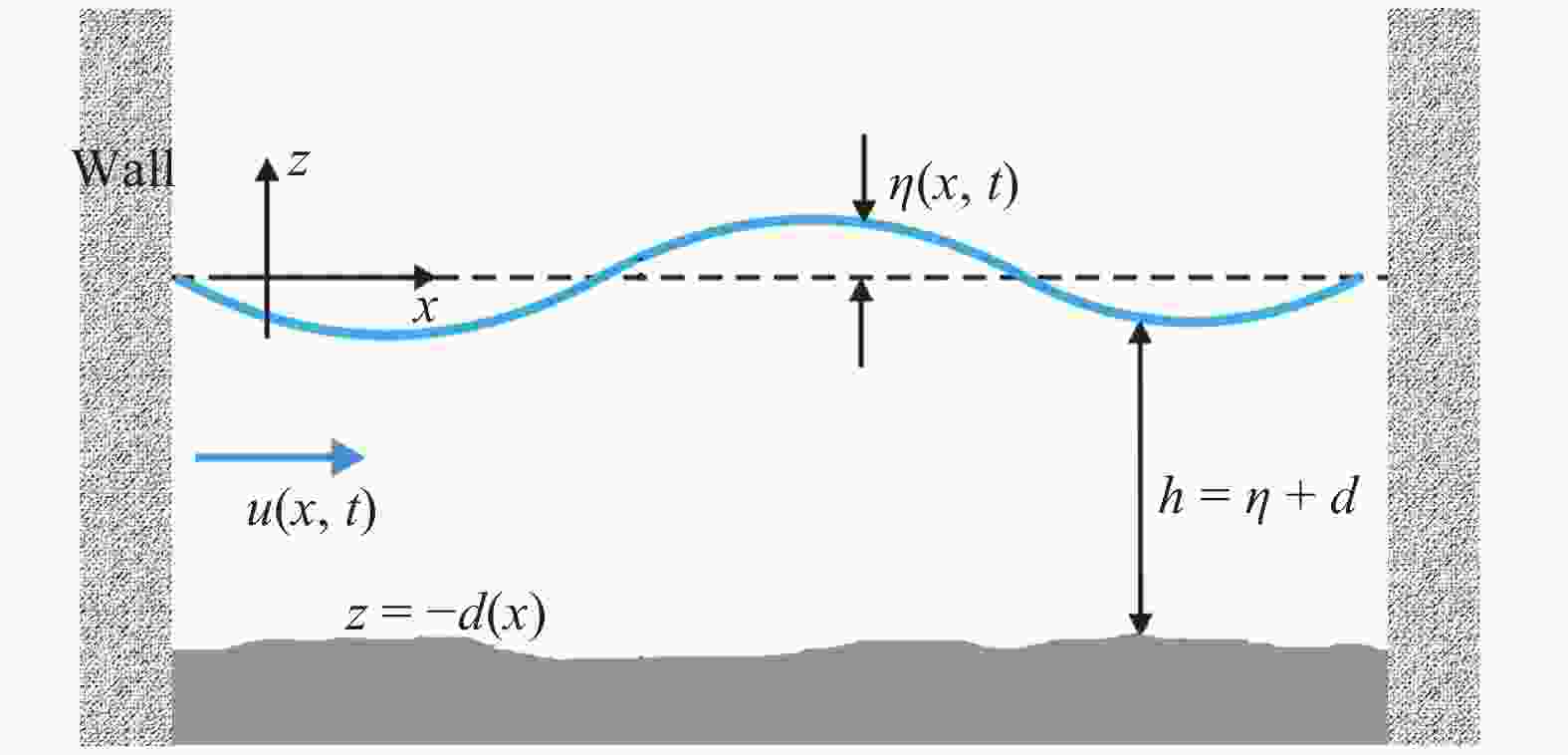
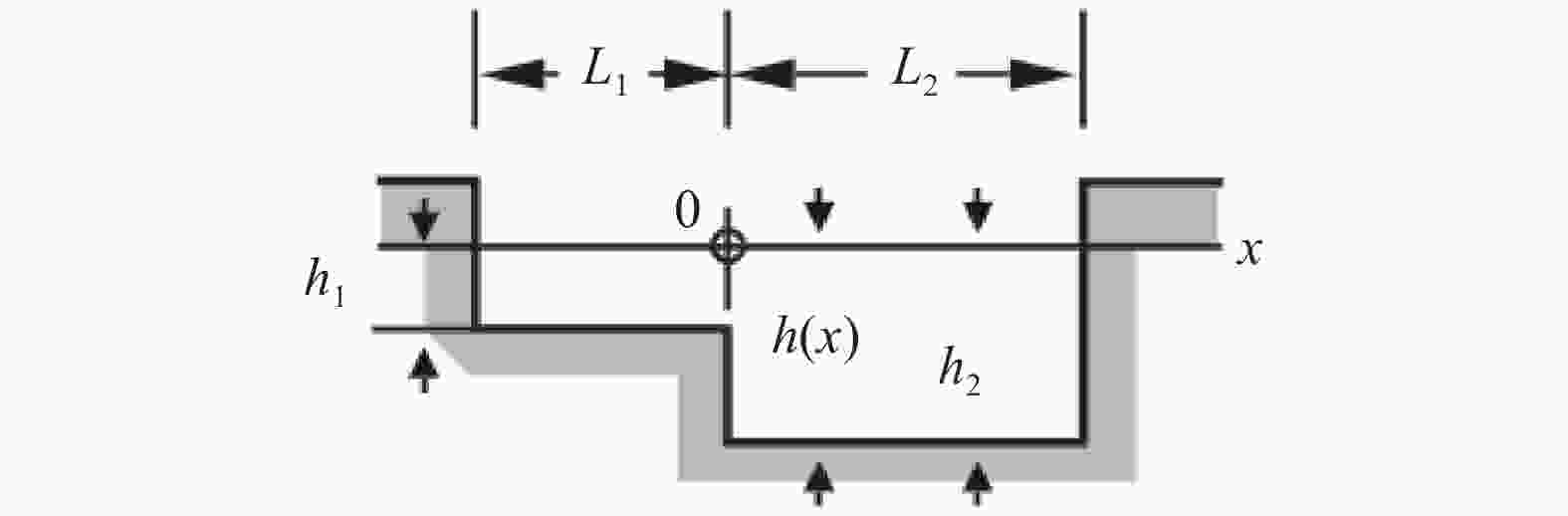
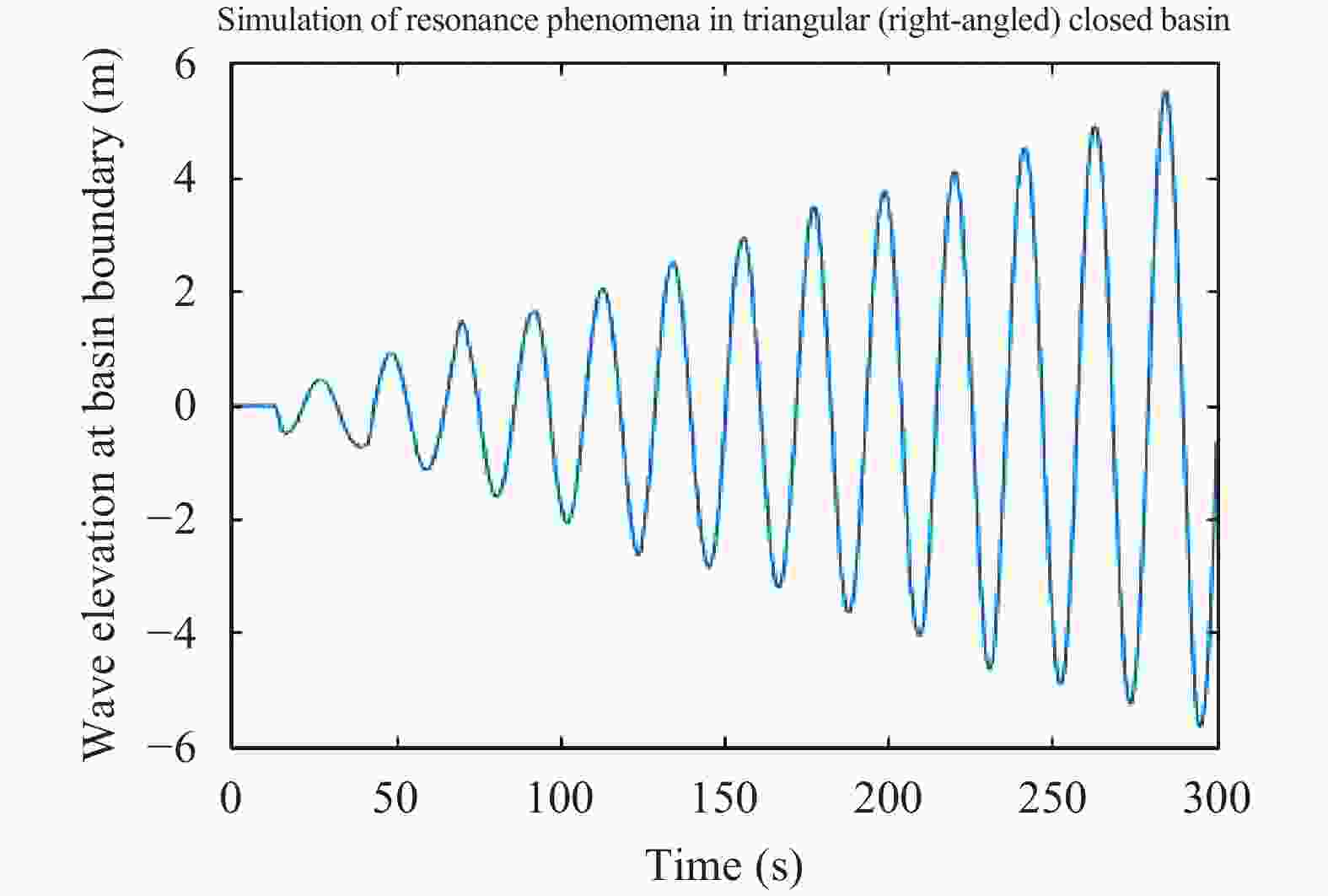
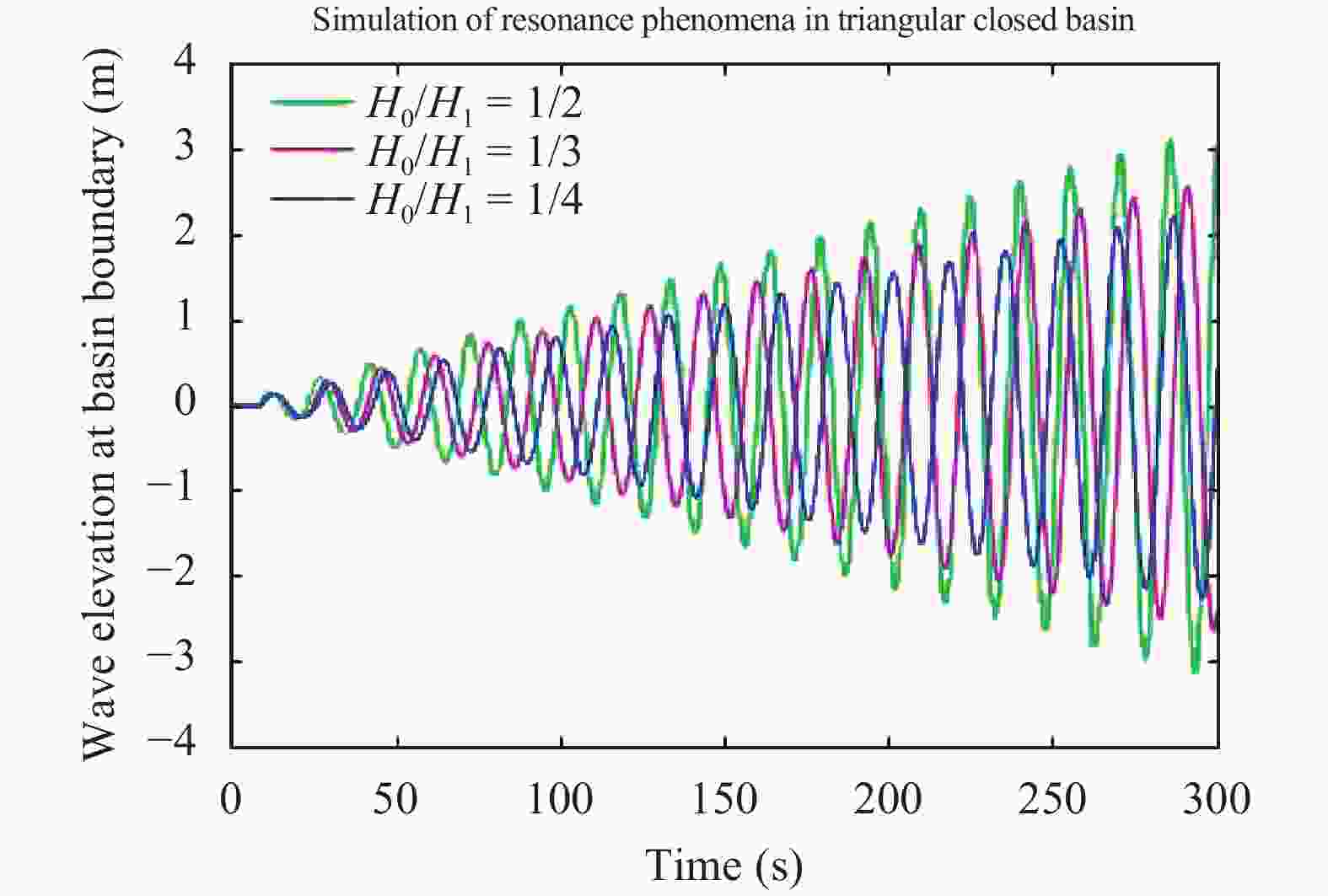
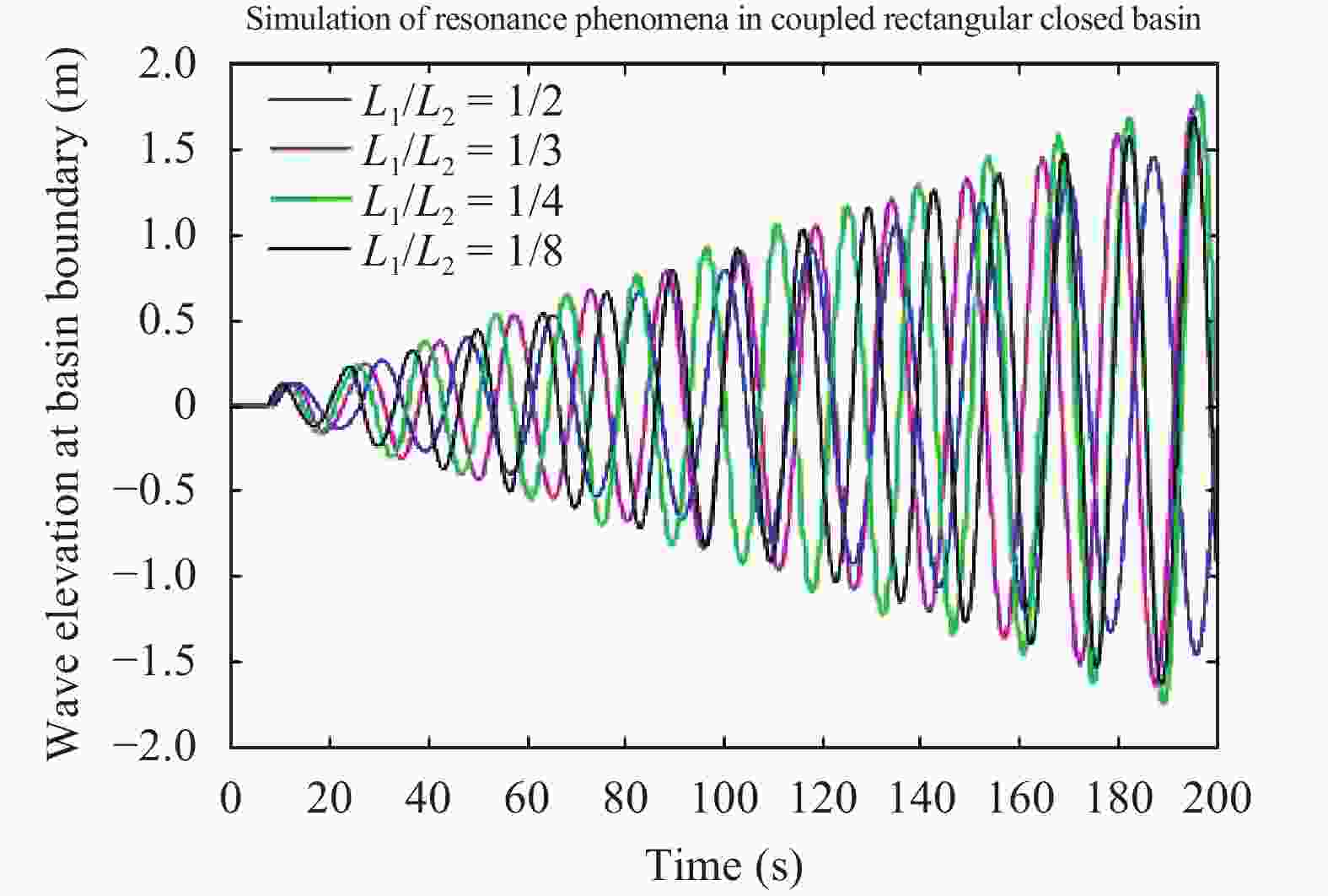
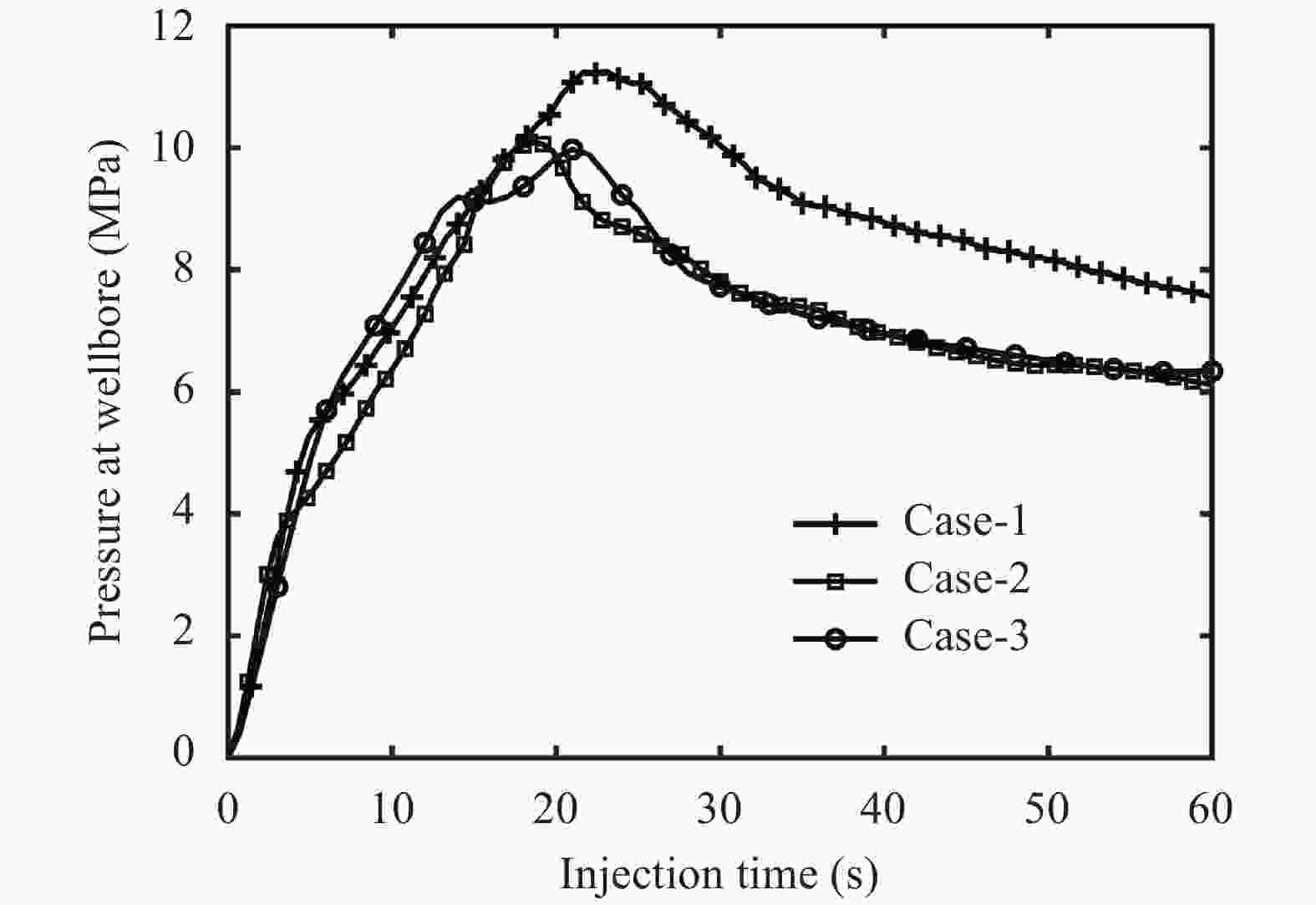
Seiches are long-period standing waves with a unique period called a natural resonant period, during which the phenomenon of resonance occurs. The occurrence of resonance in coastal areas can cause destruction to surrounding natural and man-made structures. By determining the resonant period of a given basin, we can pinpoint the conditions that allow waves to achieve resonance. In this study, a mathematical model is developed from the shallow water equations to examine seiches and resonances in various types of closed basin. The developed model is solved analytically using the separation of variables method to determine the seiches' fundamental resonant periods. Comparisons between the analytical solutions and experimental measurements for resonant periods are also provided. It is shown that the analytical resonant period confirms the experimental data for closed basin of various geometric profiles. Using a finite volume method on a staggered grid, the model is solved numerically to simulate the wave profile when resonance phenomenon occurs. Through those numerical simulations, we also obtain the fundamental resonant period for each basin which agrees with the derived analytical period.
Seiches are long-period standing waves with a unique period called a natural resonant period, during which the phenomenon of resonance occurs. The occurrence of resonance in coastal areas can cause destruction to surrounding natural and man-made structures. By determining the resonant period of a given basin, we can pinpoint the conditions that allow waves to achieve resonance. In this study, a mathematical model is developed from the shallow water equations to examine seiches and resonances in various types of closed basin. The developed model is solved analytically using the separation of variables method to determine the seiches' fundamental resonant periods. Comparisons between the analytical solutions and experimental measurements for resonant periods are also provided. It is shown that the analytical resonant period confirms the experimental data for closed basin of various geometric profiles. Using a finite volume method on a staggered grid, the model is solved numerically to simulate the wave profile when resonance phenomenon occurs. Through those numerical simulations, we also obtain the fundamental resonant period for each basin which agrees with the derived analytical period.
Theoretical and Applied Mechanics Letters 11 (2021) 100247.
doi: 10.1016/j.taml.2021.100247
Abstract:
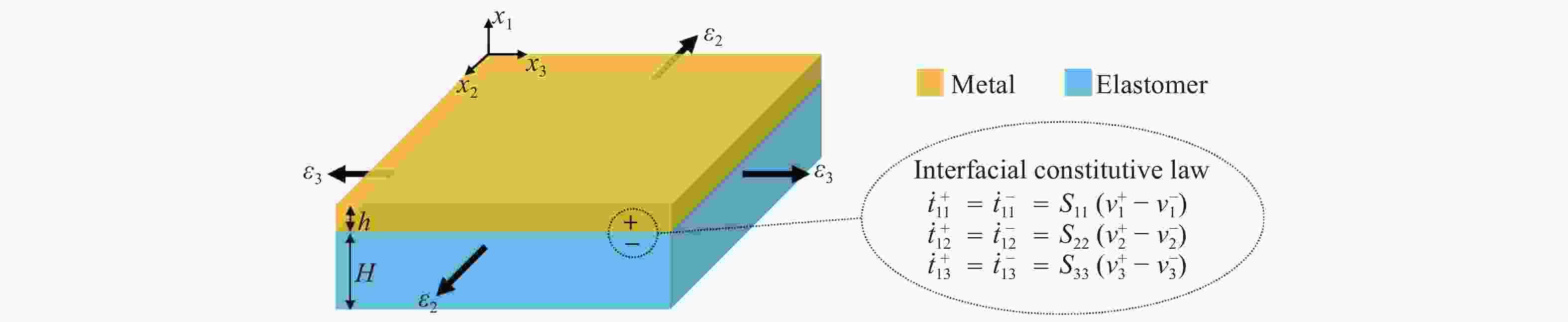
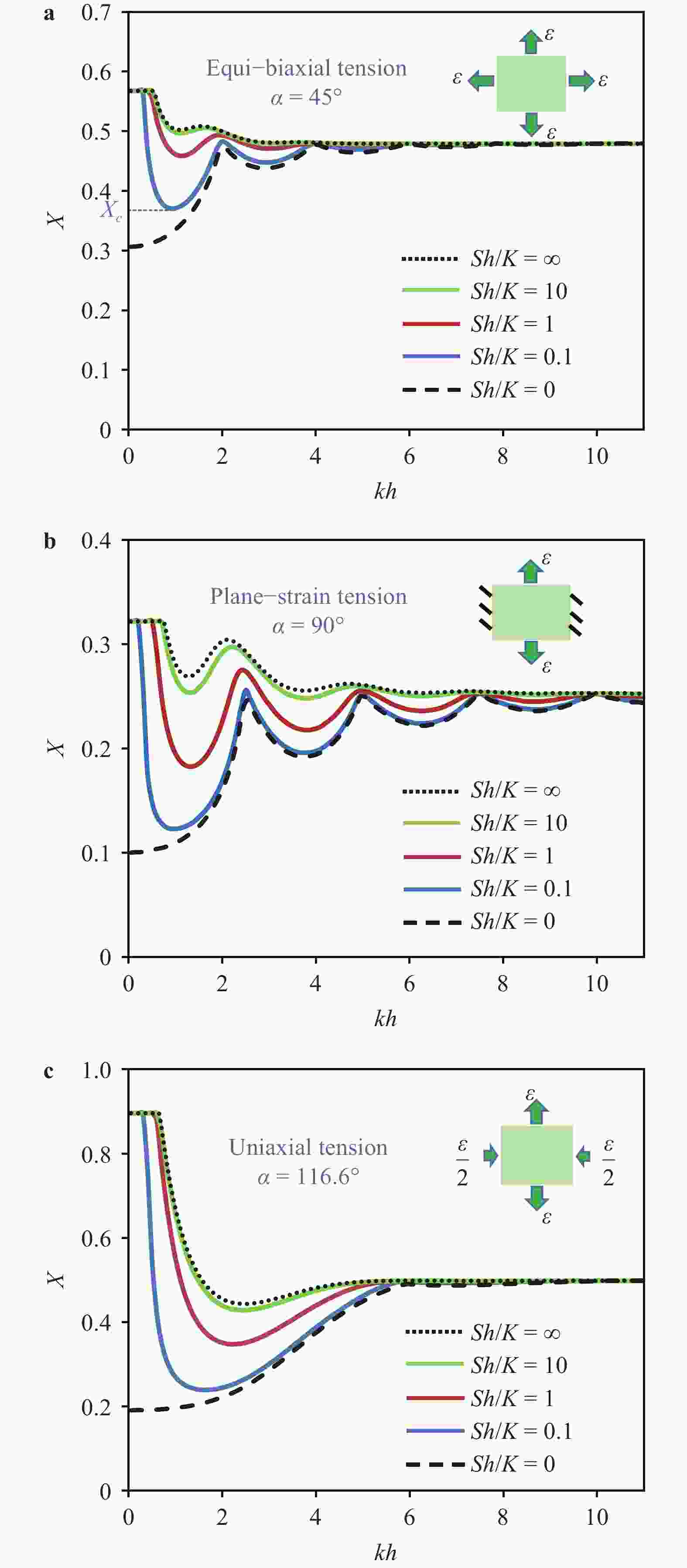
Flexible electronic devices are often subjected to large and repeated deformation, so that their functional components such as metal interconnects need to sustain strains up to tens of percent, which is far beyond the intrinsic deformability of metal materials (~1%). To meet the stringent requirements of flexible electronics, metal/elastomer bilayers, a stretchable structure that consists of a metal film adhered to a stretchable elastomer substrate, have been developed to improve the stretch capability of metal interconnects. Previous studies have predicted that the metal/elastomer bilayers are much more stretchable than freestanding metal films. However, these investigations usually assume perfect bonding between the metal and elastomer layers. In this work, the effect of the metal/elastomer interface with a finite interfacial stiffness on the stretchability of bilayer structures is analyzed. The results show that the assumption of perfect interface (with infinite interfacial stiffness) may lead to an overestimation of the stretchability of bilayer structures. It is also demonstrated that increased adhesion between the metal and elastomer layers can enhance the stretchability of the metal layer.
Flexible electronic devices are often subjected to large and repeated deformation, so that their functional components such as metal interconnects need to sustain strains up to tens of percent, which is far beyond the intrinsic deformability of metal materials (~1%). To meet the stringent requirements of flexible electronics, metal/elastomer bilayers, a stretchable structure that consists of a metal film adhered to a stretchable elastomer substrate, have been developed to improve the stretch capability of metal interconnects. Previous studies have predicted that the metal/elastomer bilayers are much more stretchable than freestanding metal films. However, these investigations usually assume perfect bonding between the metal and elastomer layers. In this work, the effect of the metal/elastomer interface with a finite interfacial stiffness on the stretchability of bilayer structures is analyzed. The results show that the assumption of perfect interface (with infinite interfacial stiffness) may lead to an overestimation of the stretchability of bilayer structures. It is also demonstrated that increased adhesion between the metal and elastomer layers can enhance the stretchability of the metal layer.
Theoretical and Applied Mechanics Letters 11 (2021) 100252.
doi: 10.1016/j.taml.2021.100252
Abstract:
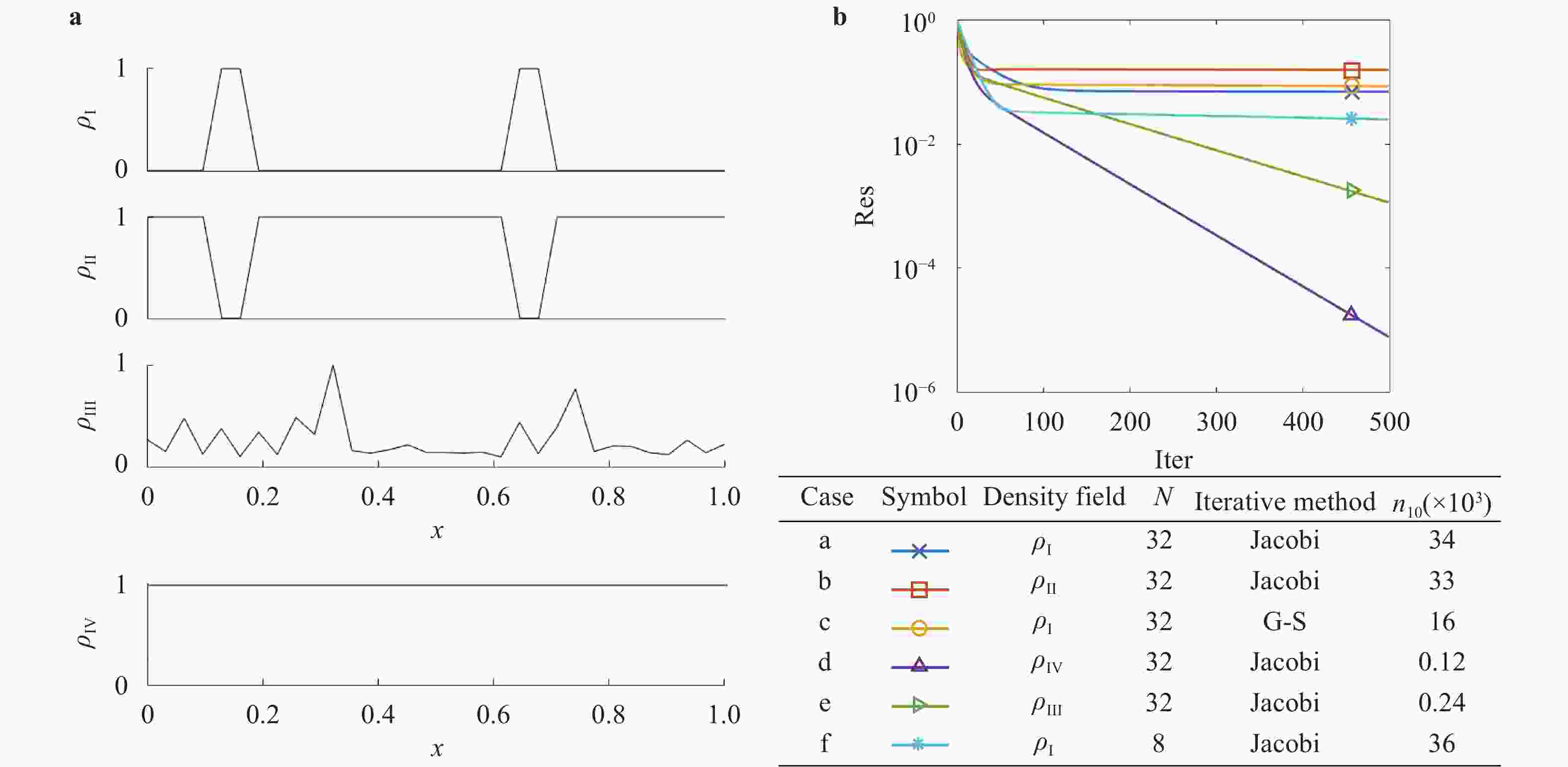
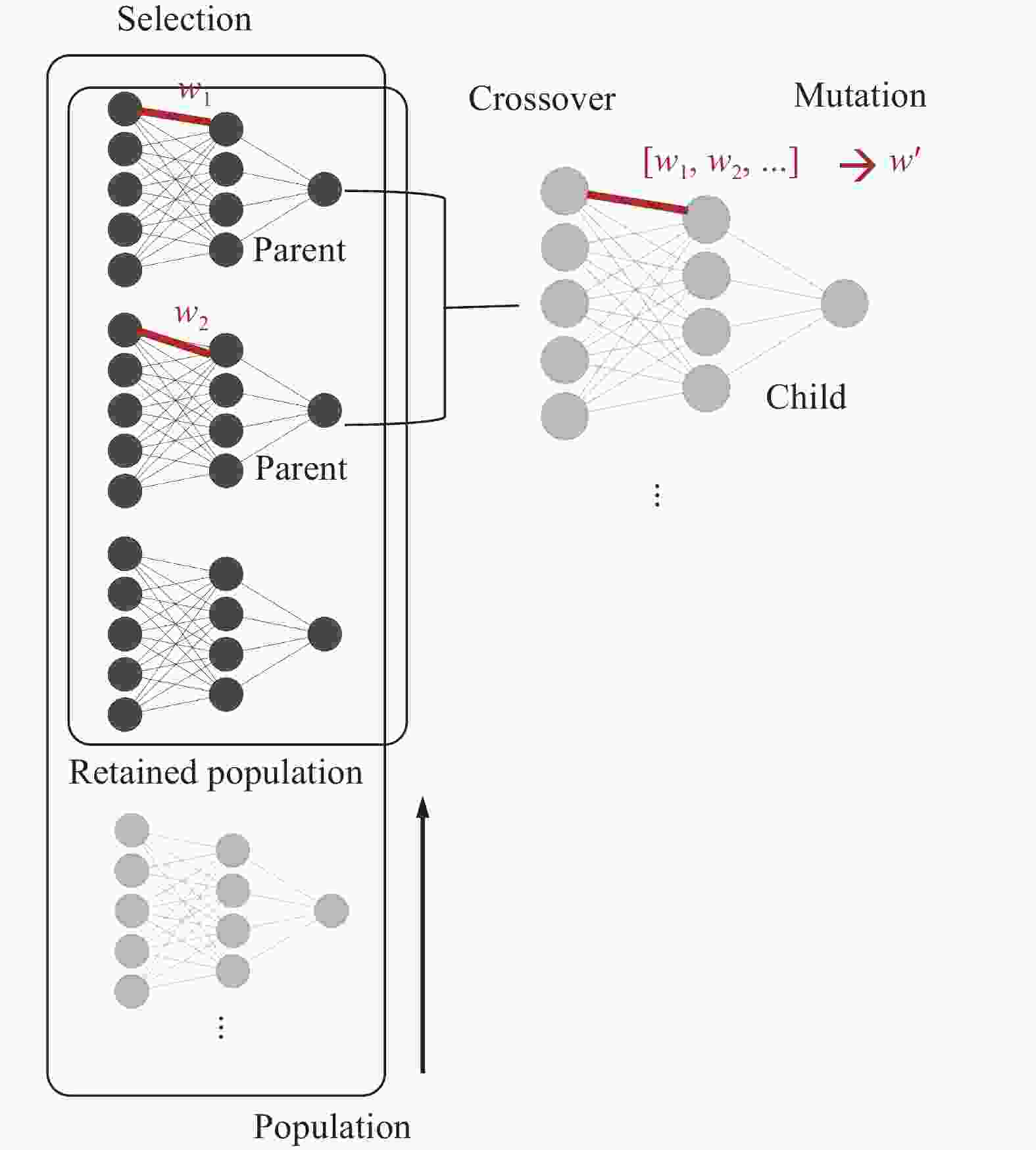
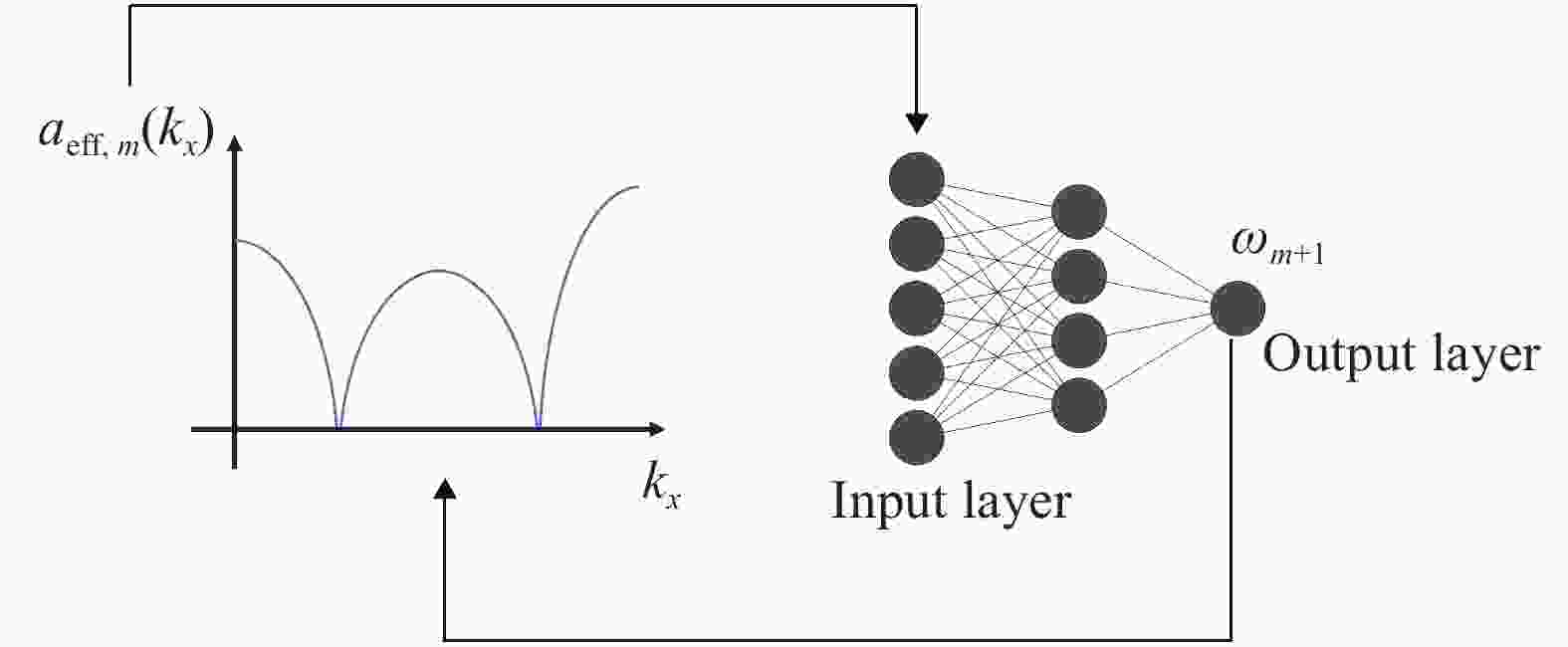
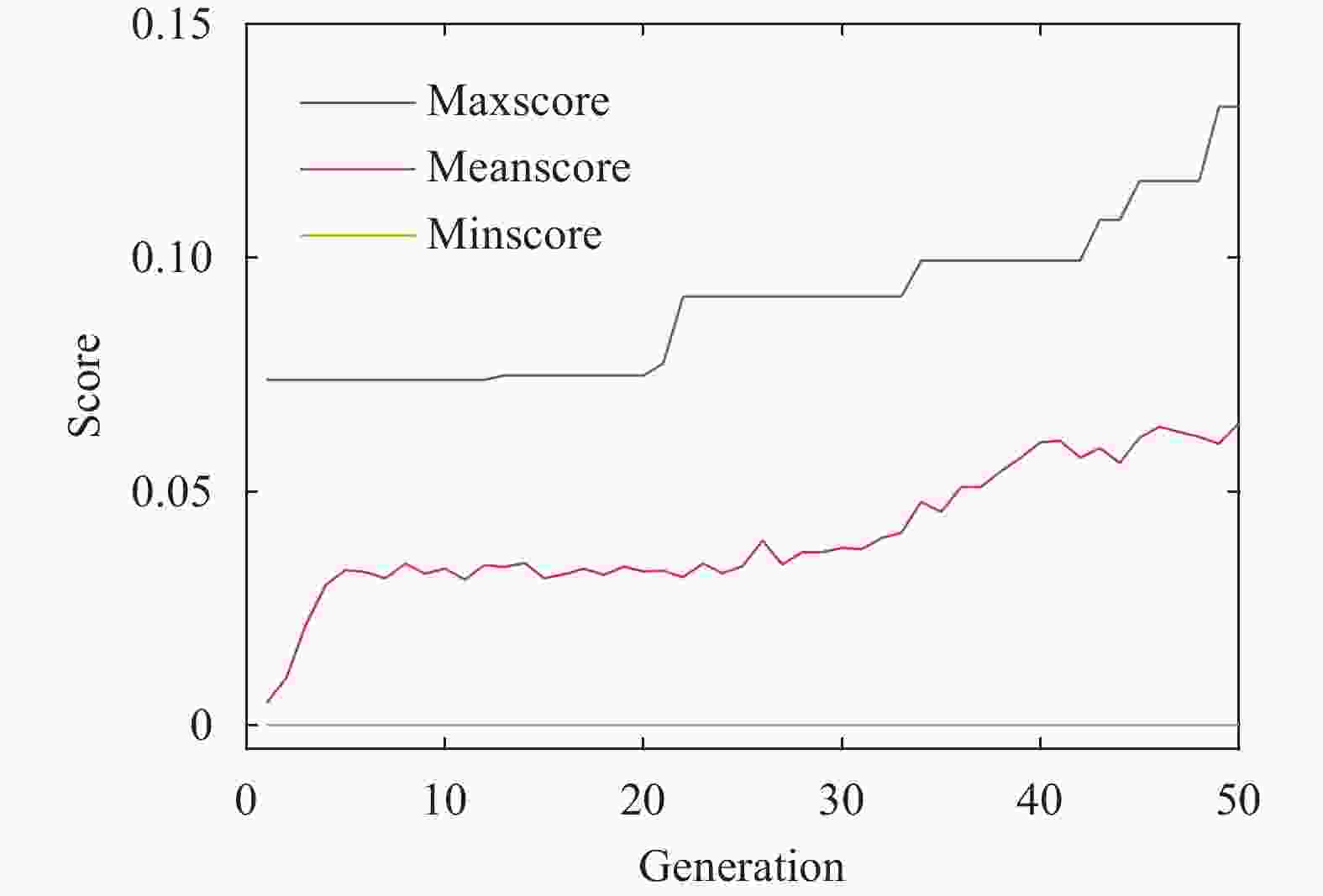
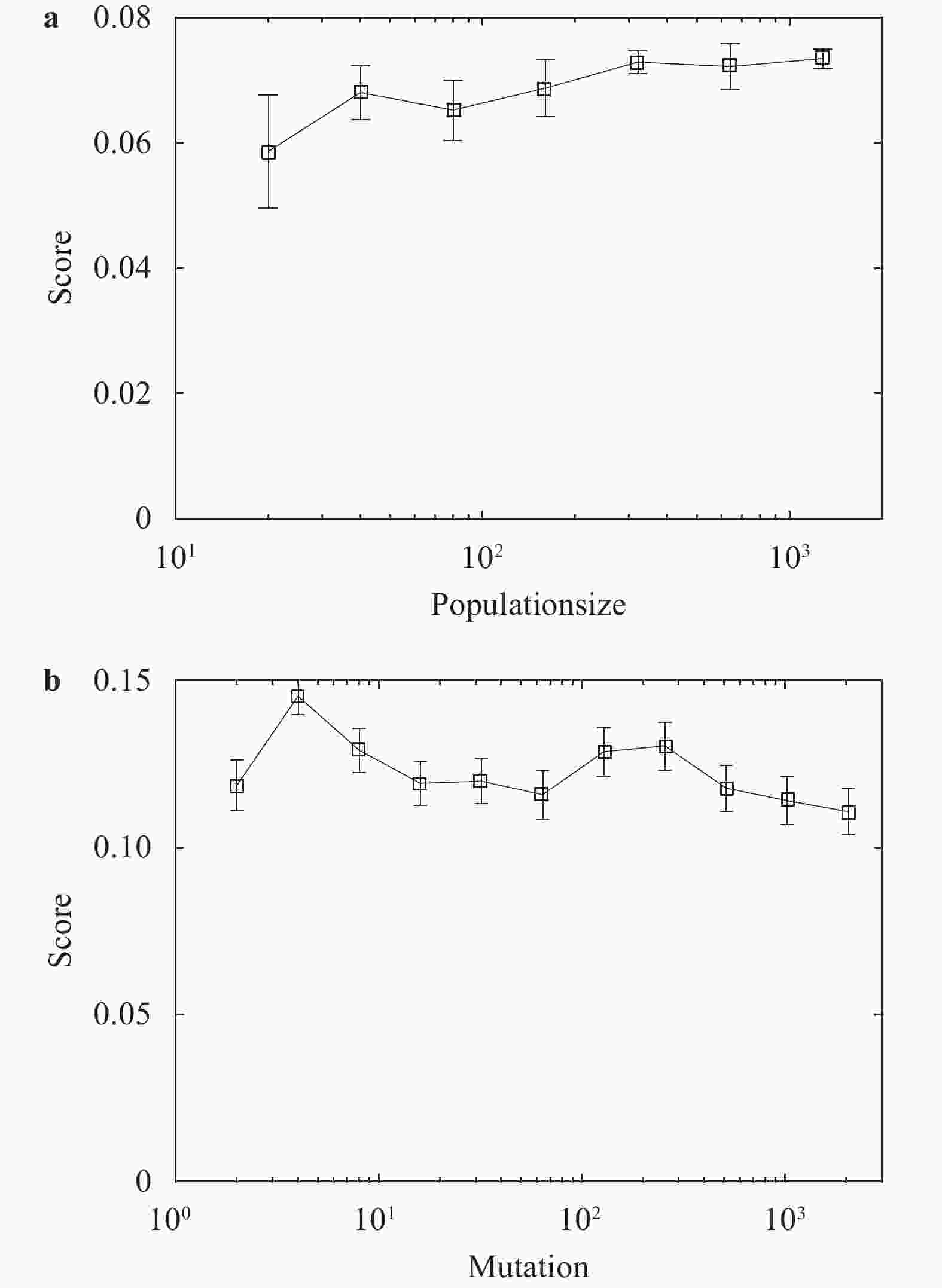
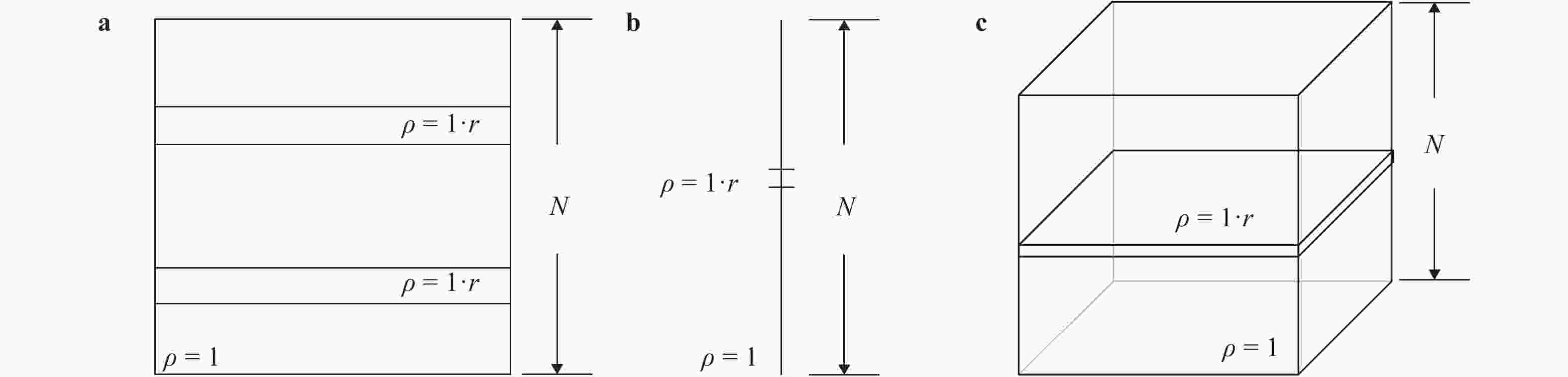
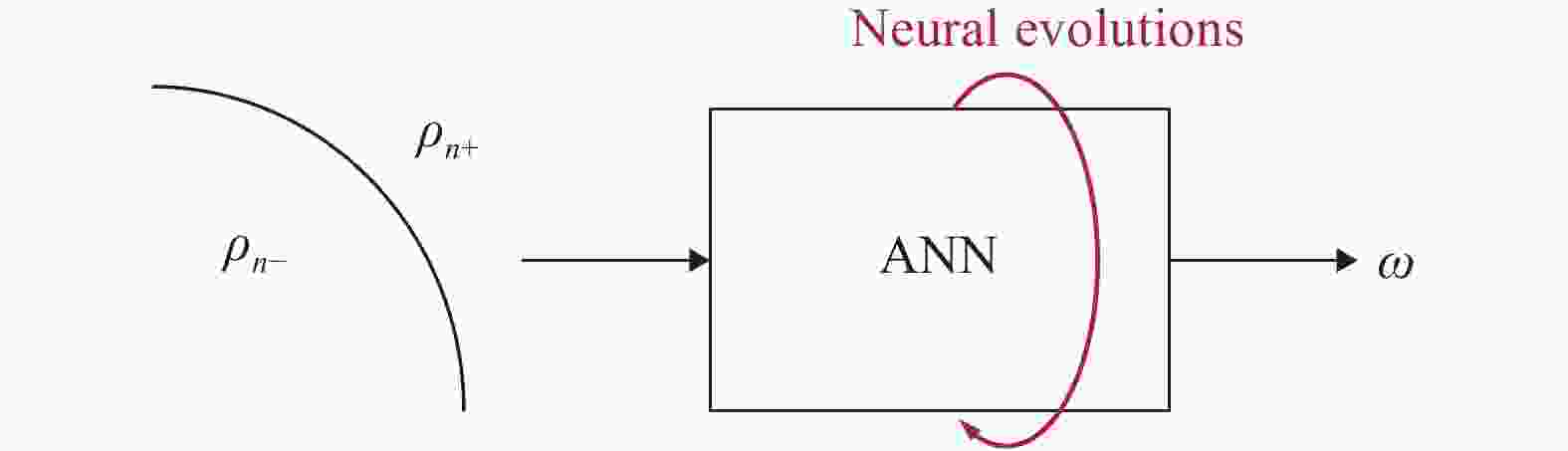
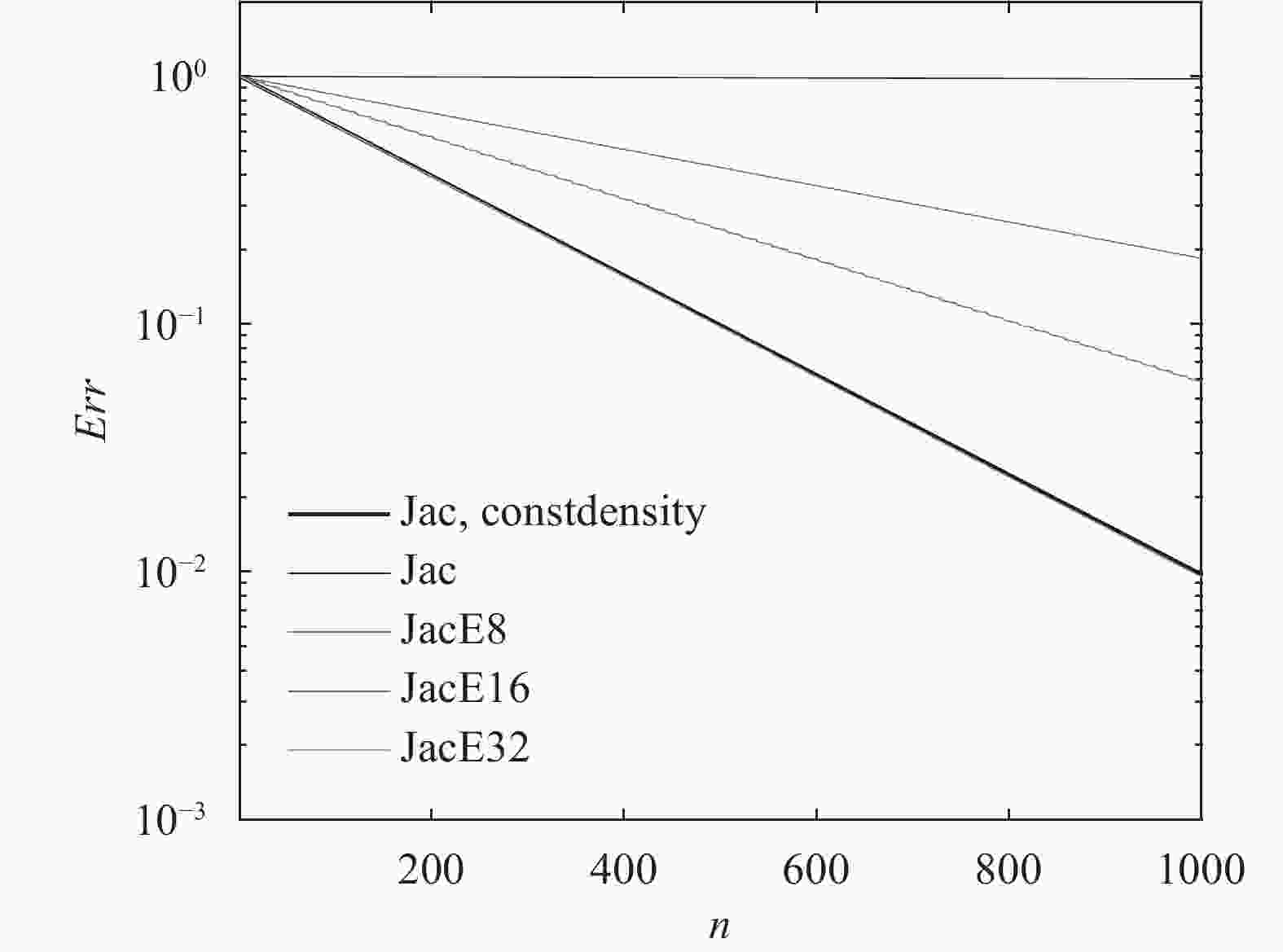
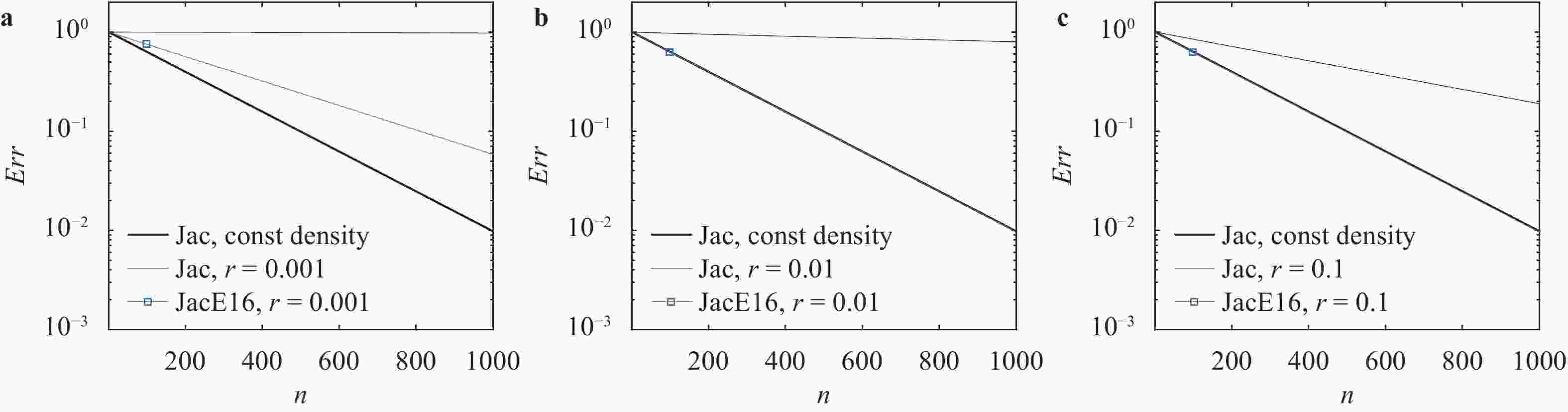
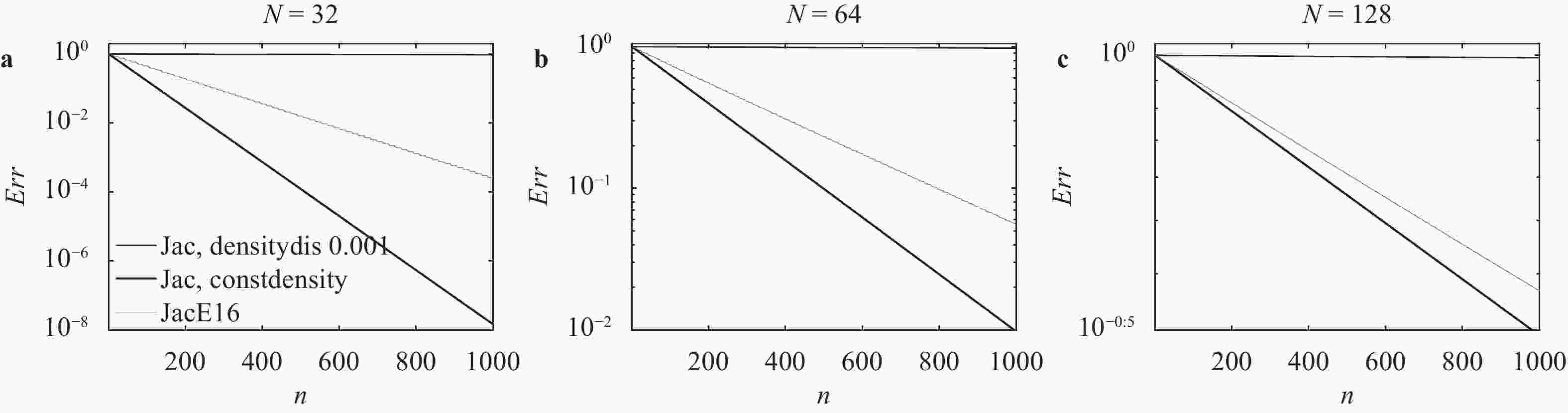
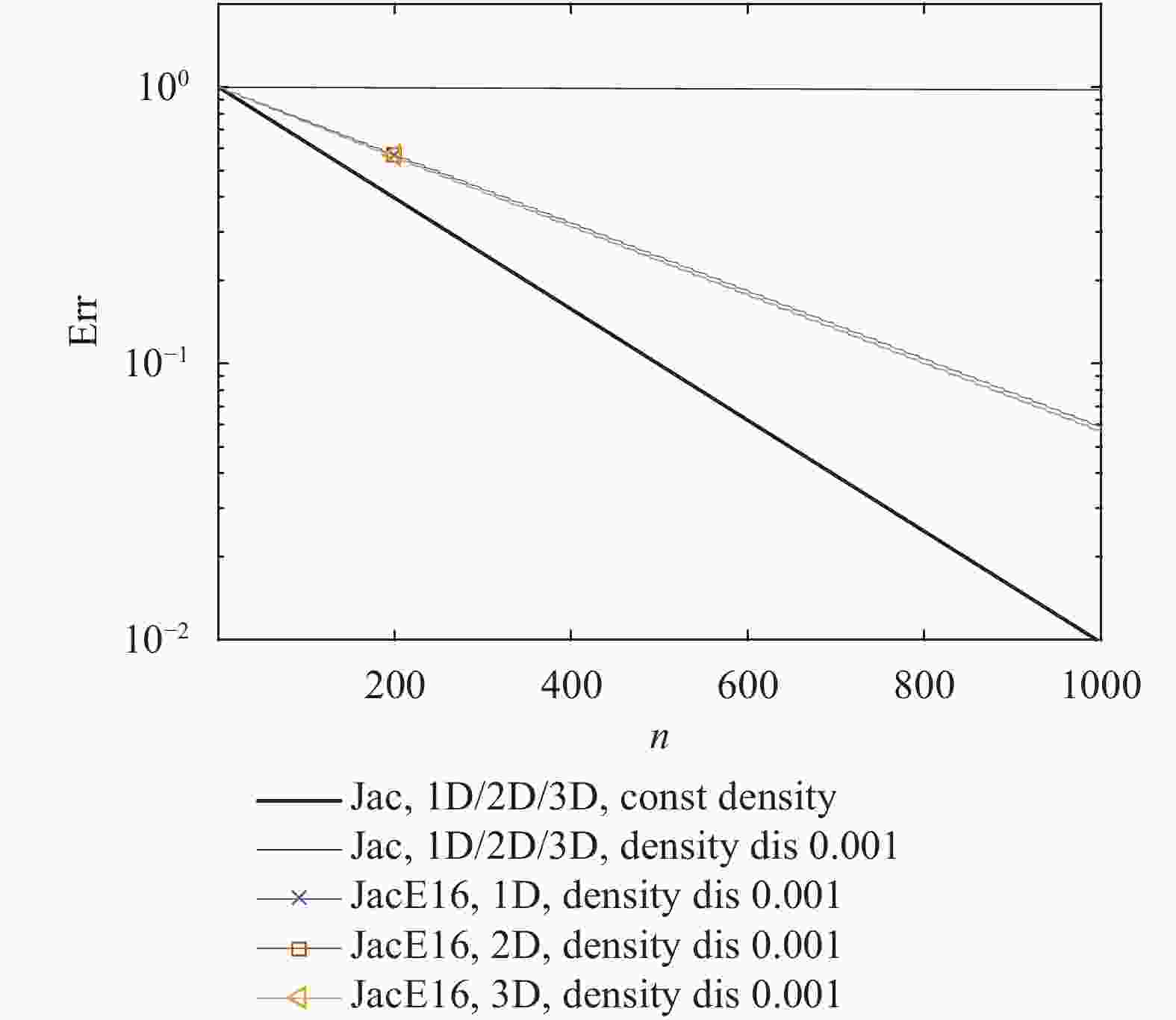
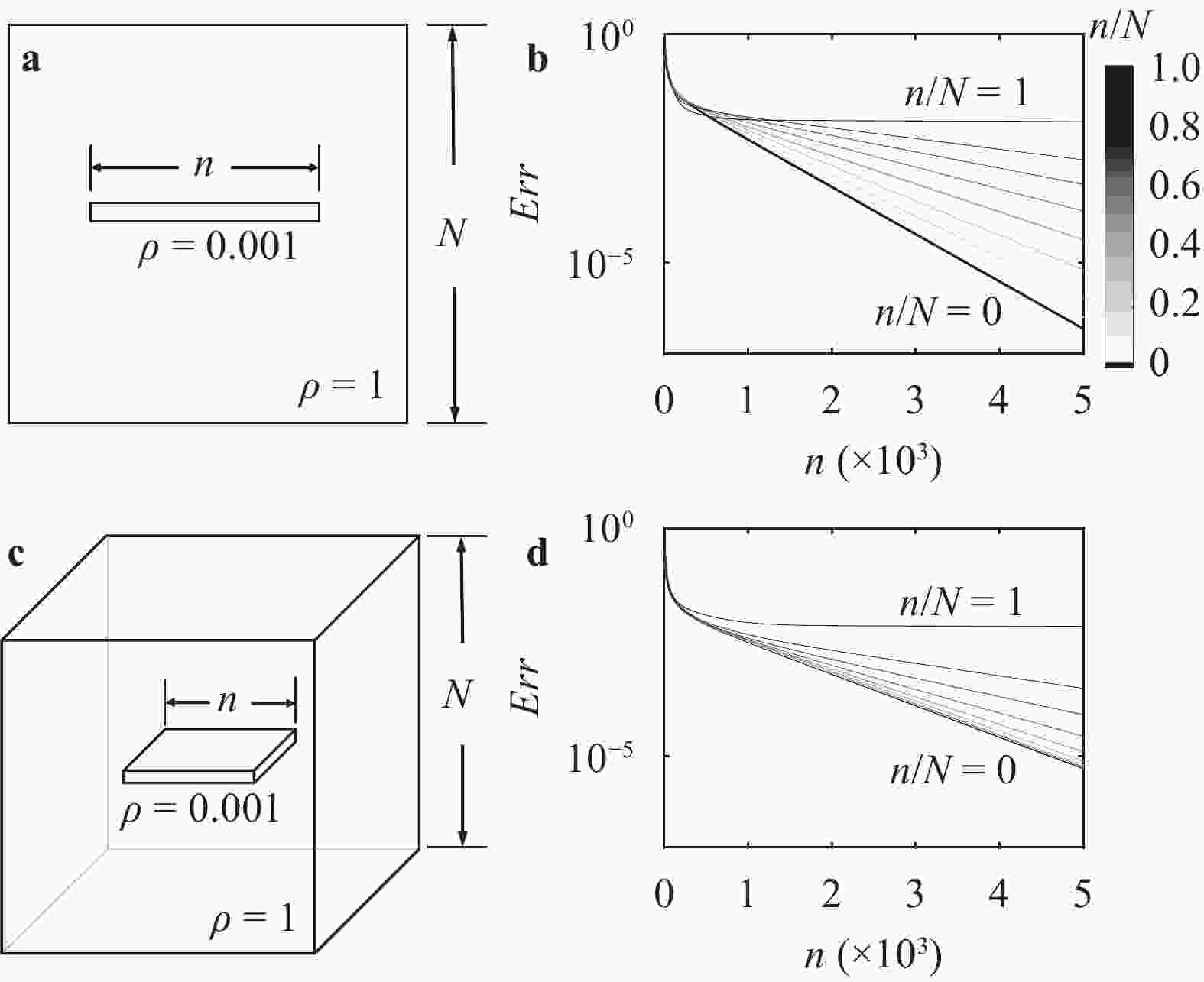
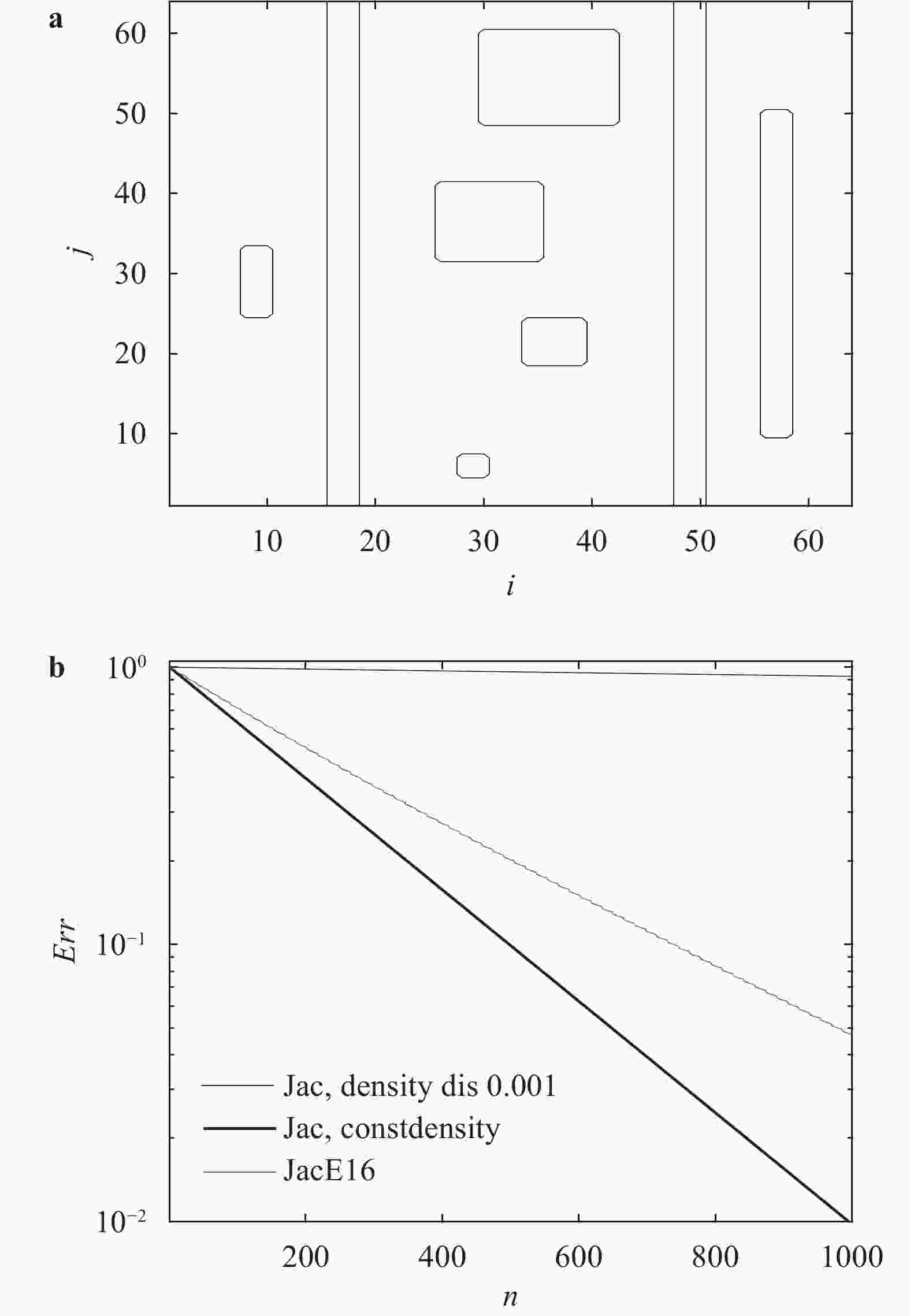
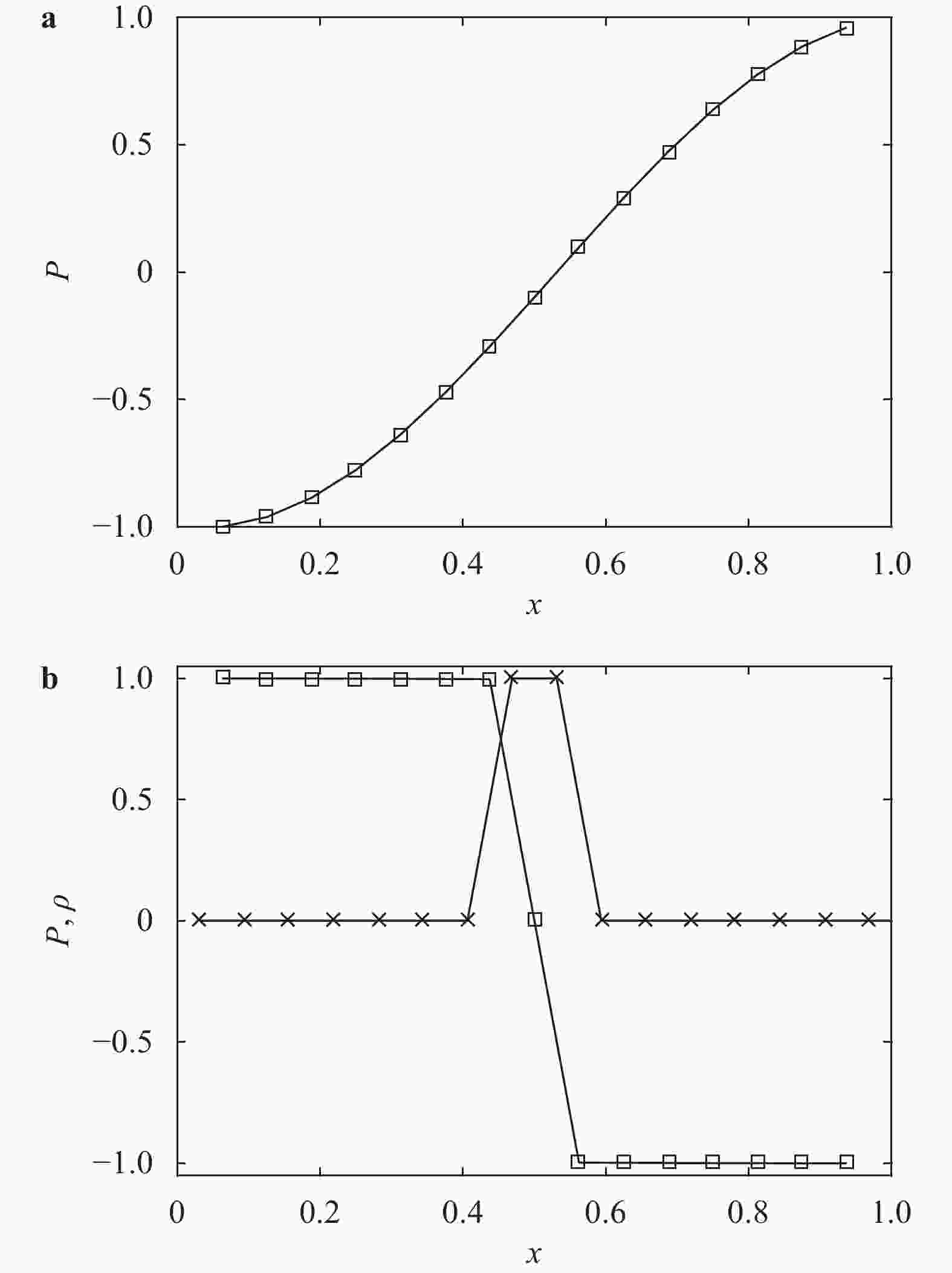
Lacking labeled examples of working numerical strategies, adapting an iterative solver to accommodate a numerical issue, e.g., density discontinuities in the pressure Poisson equation, is non-trivial and usually involves a lot of trial and error. Here, we resort to evolutionary neural network. A evolutionary neural network observes the outcome of an action and adapts its strategy accordingly. The process requires no labeled data but only a measure of a network’s performance at a task. Applying neuro-evolution and adapting the Jacobi iterative method for the pressure Poisson equation with density discontinuities, we show that the adapted Jacobi method is able to accommodate density discontinuities.
Lacking labeled examples of working numerical strategies, adapting an iterative solver to accommodate a numerical issue, e.g., density discontinuities in the pressure Poisson equation, is non-trivial and usually involves a lot of trial and error. Here, we resort to evolutionary neural network. A evolutionary neural network observes the outcome of an action and adapts its strategy accordingly. The process requires no labeled data but only a measure of a network’s performance at a task. Applying neuro-evolution and adapting the Jacobi iterative method for the pressure Poisson equation with density discontinuities, we show that the adapted Jacobi method is able to accommodate density discontinuities.
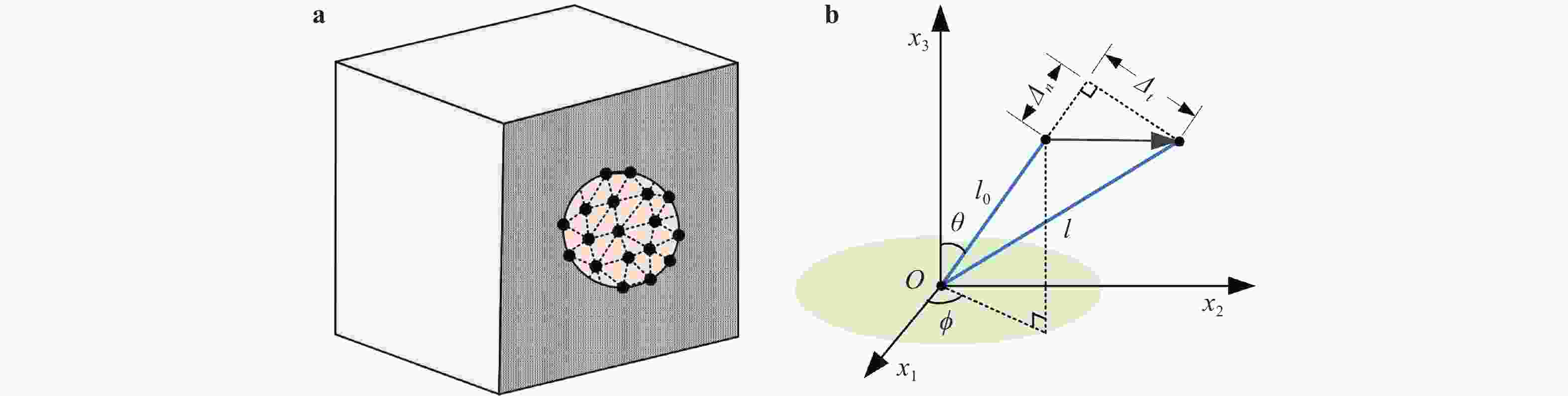
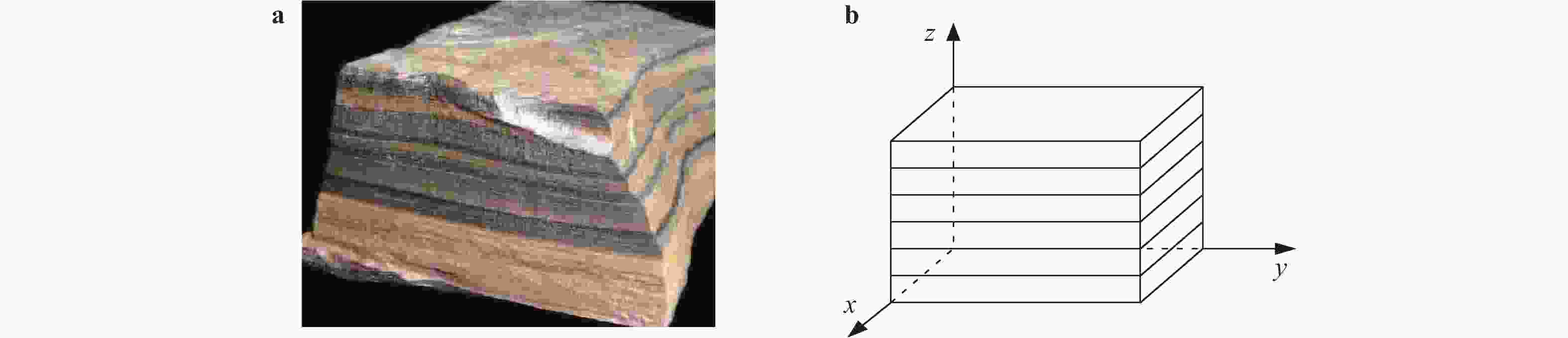
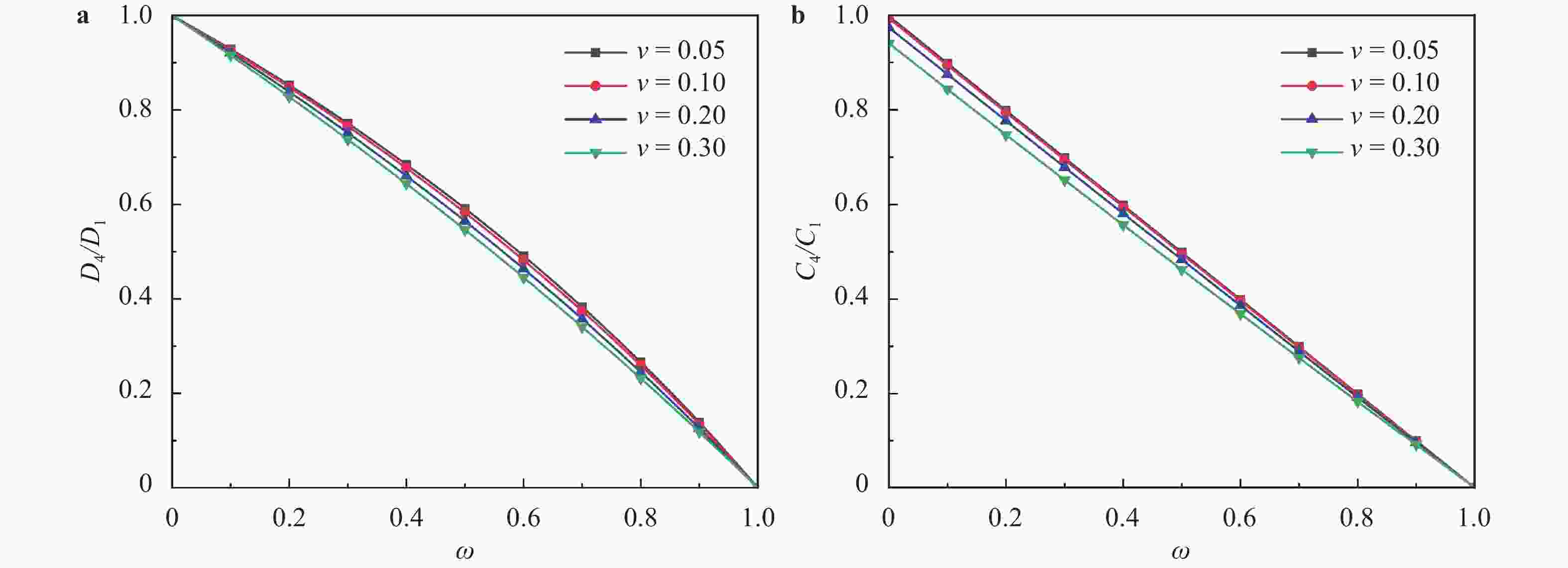
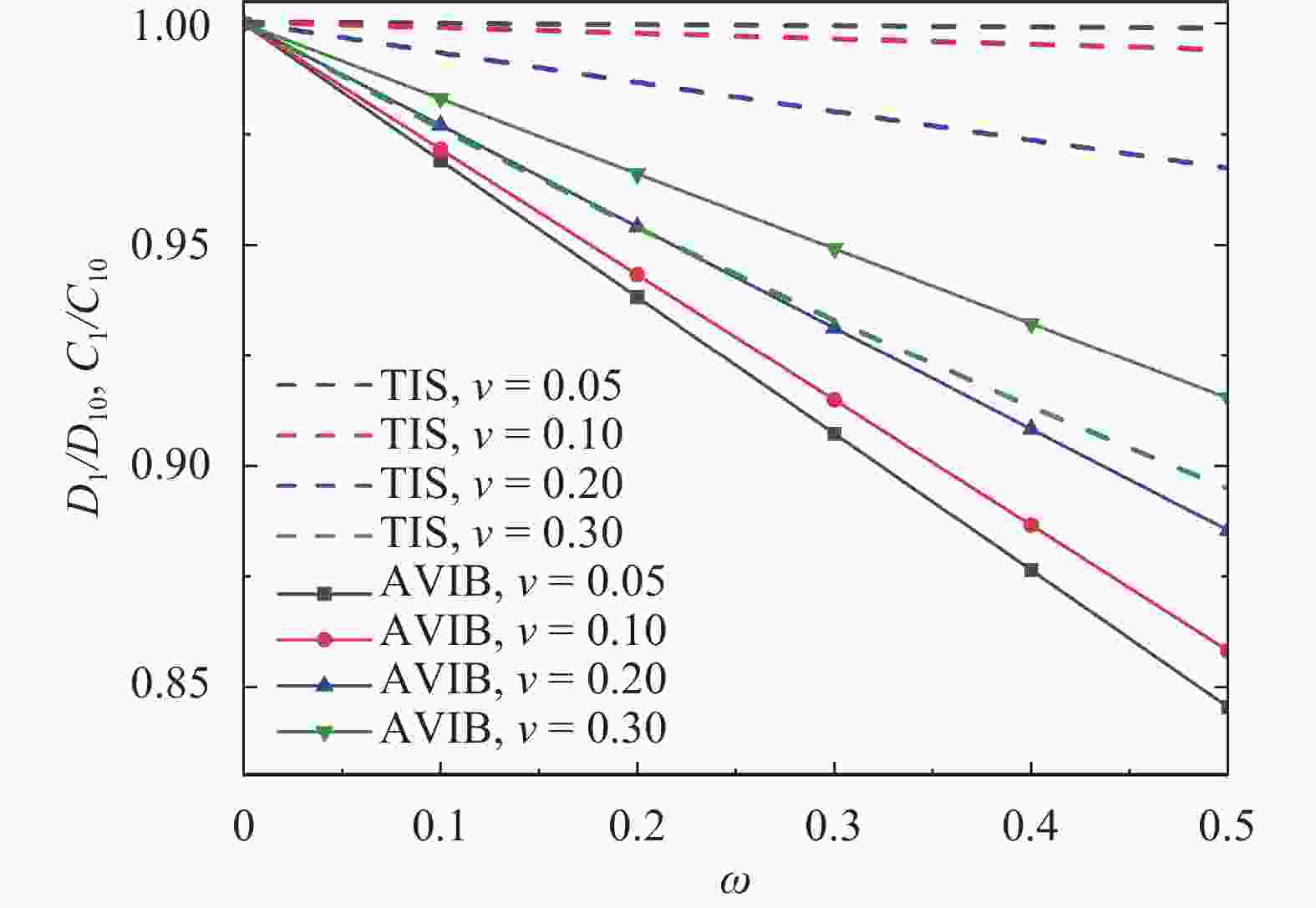
Bedding plane-embedded augmented virtual internal bonds for fracture propagation simulation in shale
Theoretical and Applied Mechanics Letters 11 (2021) 100253.
doi: 10.1016/j.taml.2021.100253
Abstract:
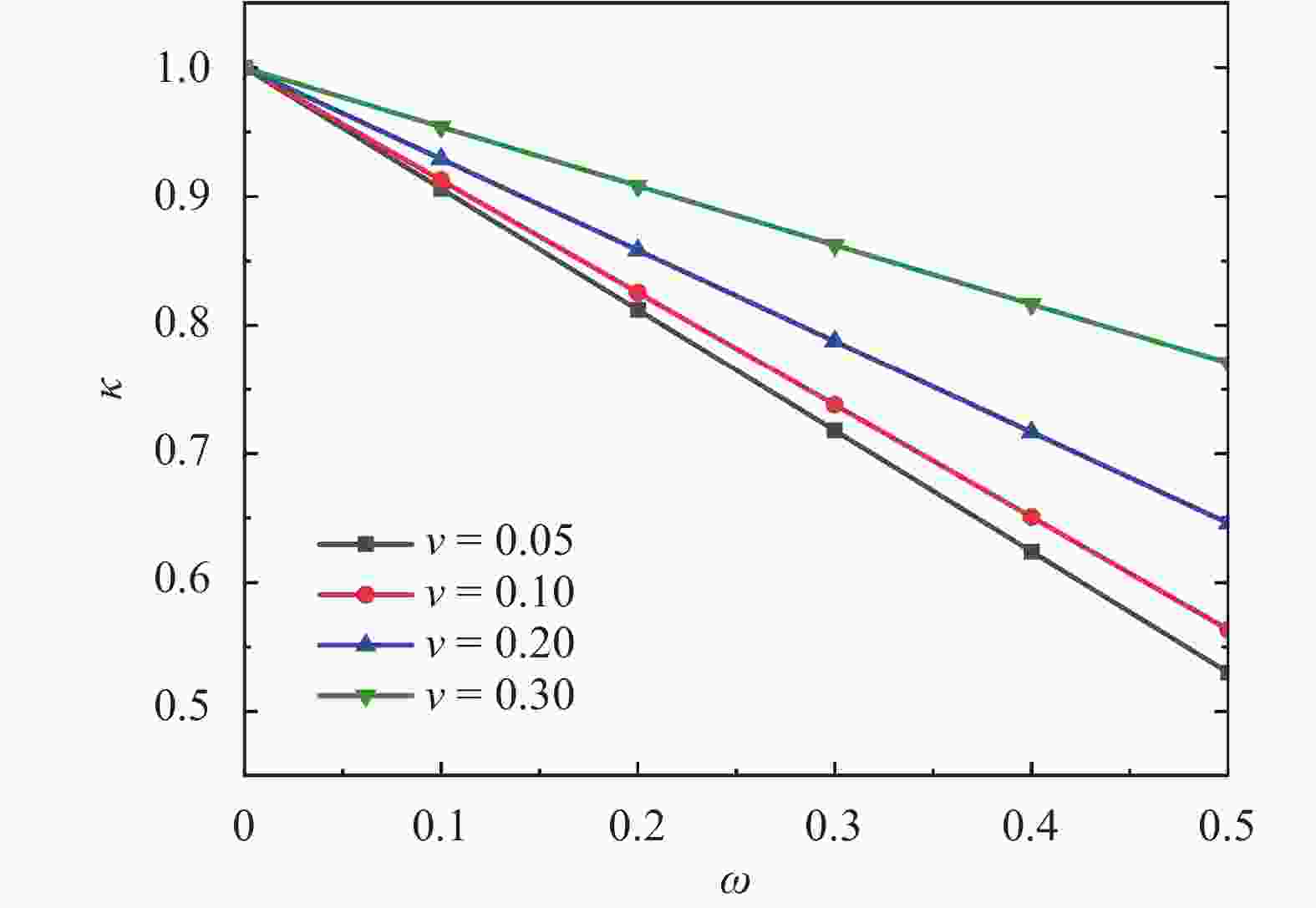
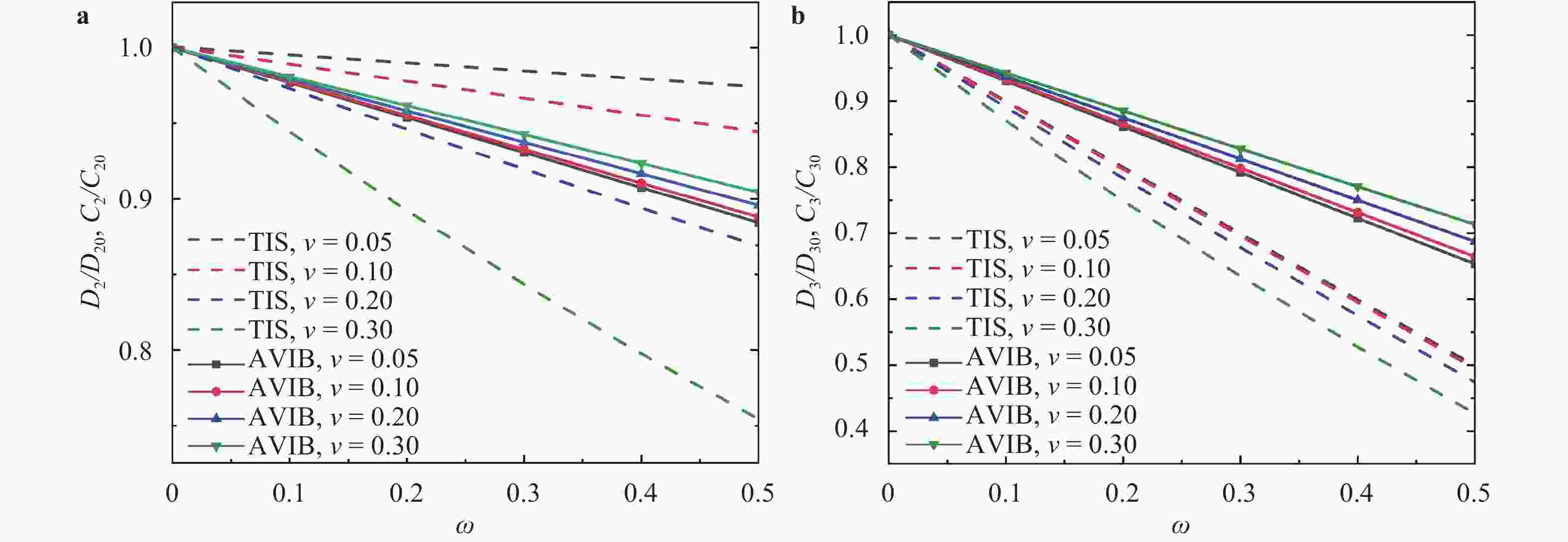
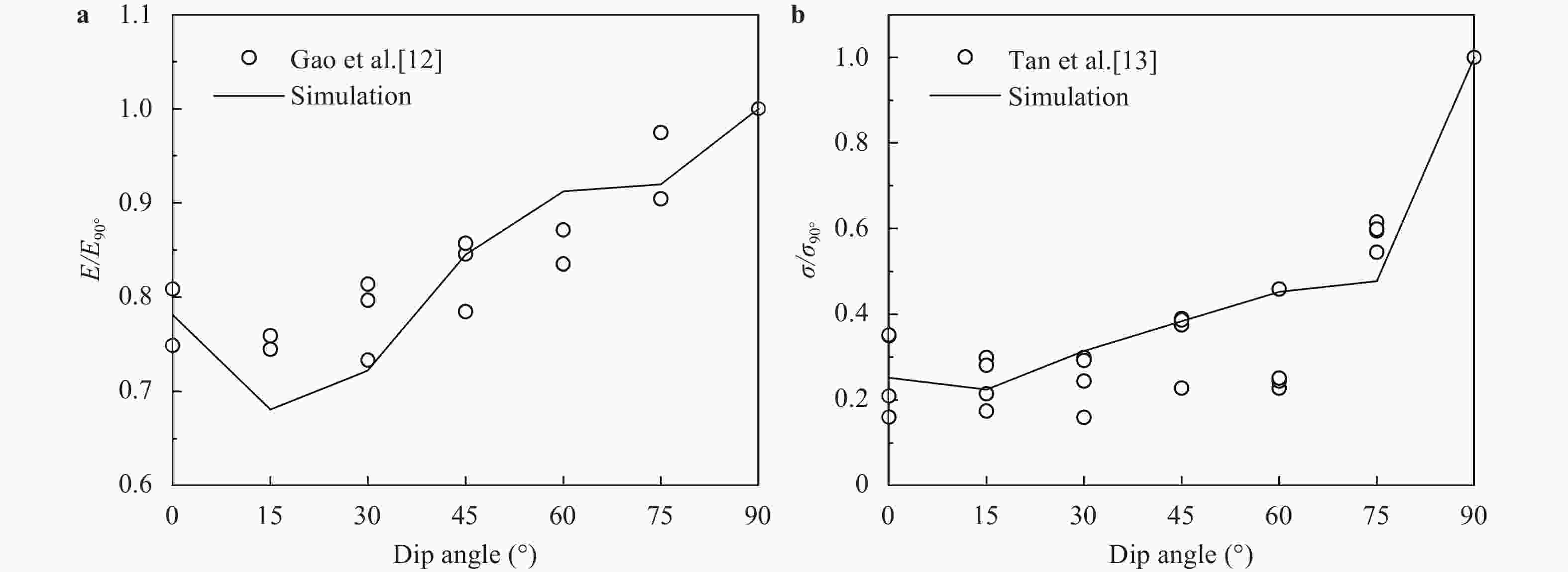
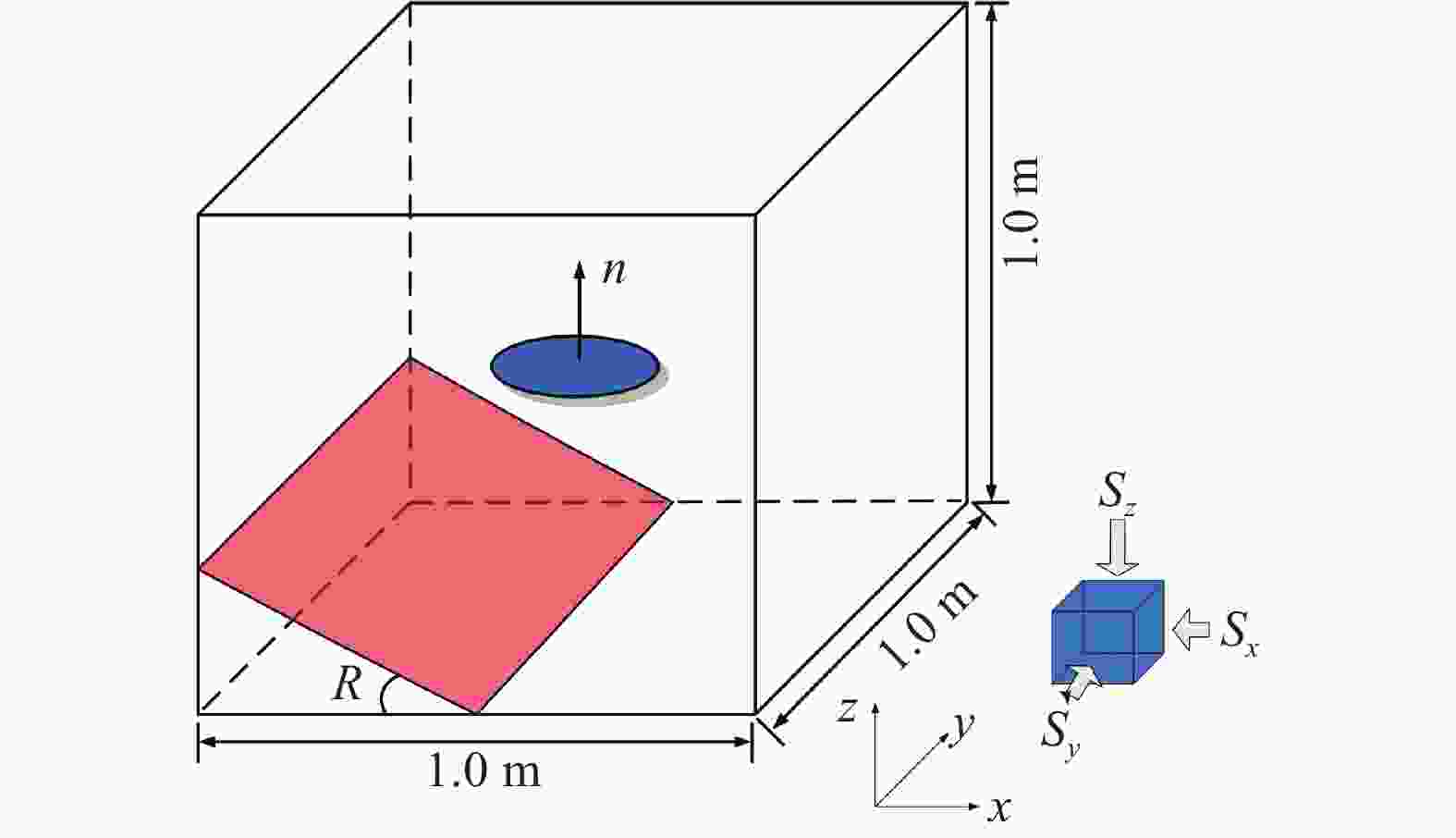
To effectively simulate the fracture propagation in shale, the bedding plane (BP) effect is incorporated into the augmented virtual internal bond (AVIB) constitutive relation through BP tensor. Comparing the BP-embedded AVIB with the theory of transverse isotropy, it is found the approach can represent the anisotropic properties induced by parallel BPs. Through the simulation example, it is found that this method can simulate the stiffness anisotropy of shale and can represent the effect of BPs on hydraulic fracture propagation direction. Compared with the BP-embedded VIB, this method can account for the various Poisson's ratio. It provides a feasible approach to simulate the fracture propagation in shale.
To effectively simulate the fracture propagation in shale, the bedding plane (BP) effect is incorporated into the augmented virtual internal bond (AVIB) constitutive relation through BP tensor. Comparing the BP-embedded AVIB with the theory of transverse isotropy, it is found the approach can represent the anisotropic properties induced by parallel BPs. Through the simulation example, it is found that this method can simulate the stiffness anisotropy of shale and can represent the effect of BPs on hydraulic fracture propagation direction. Compared with the BP-embedded VIB, this method can account for the various Poisson's ratio. It provides a feasible approach to simulate the fracture propagation in shale.
Theoretical and Applied Mechanics Letters 11 (2021) 100249.
doi: 10.1016/j.taml.2021.000249
Abstract:
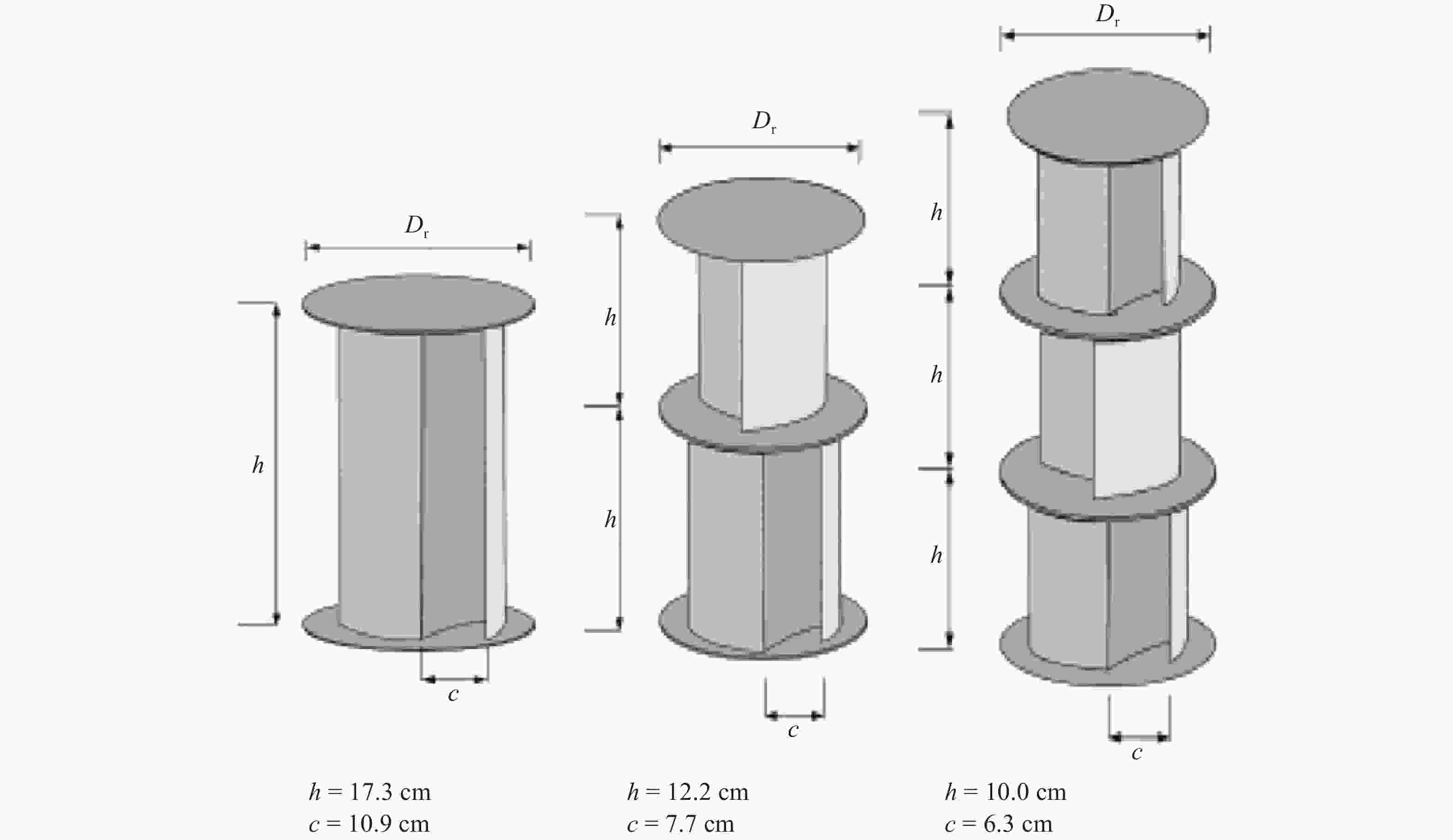
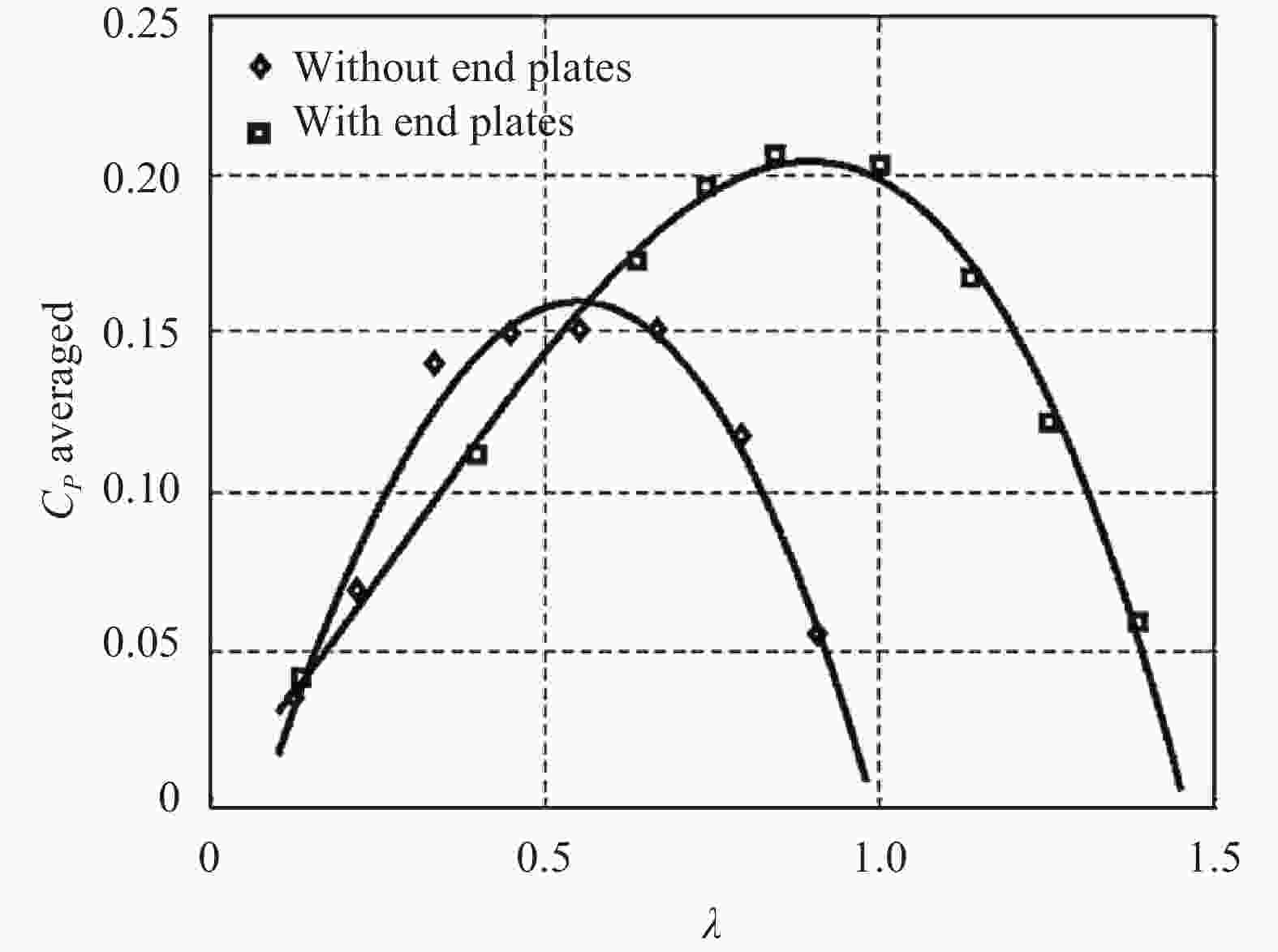
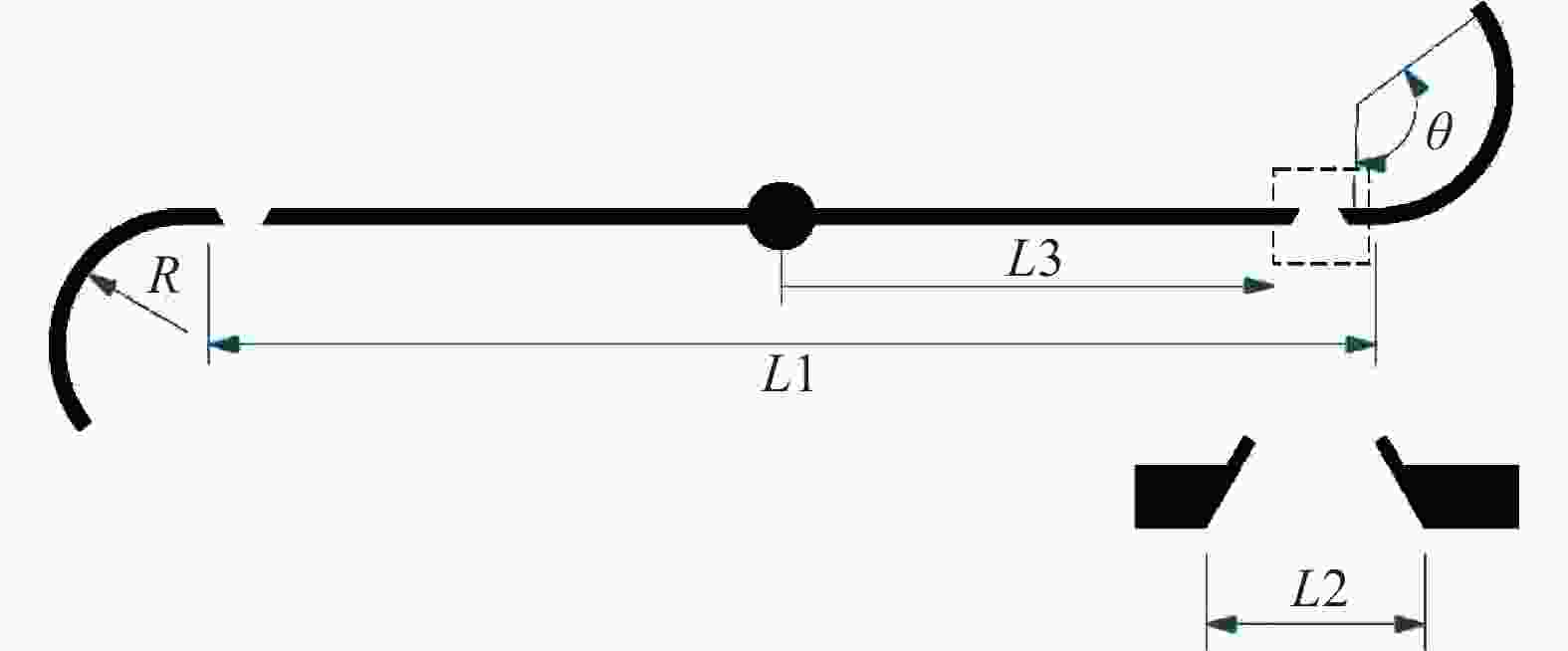
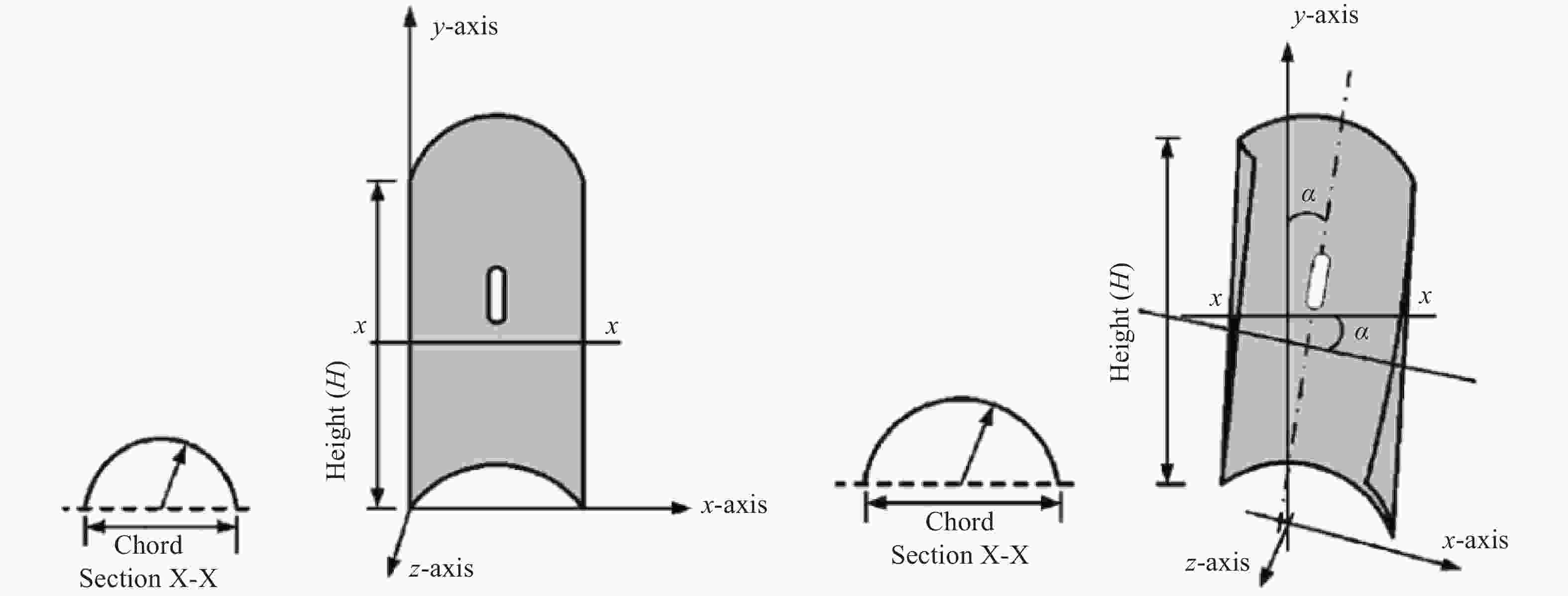
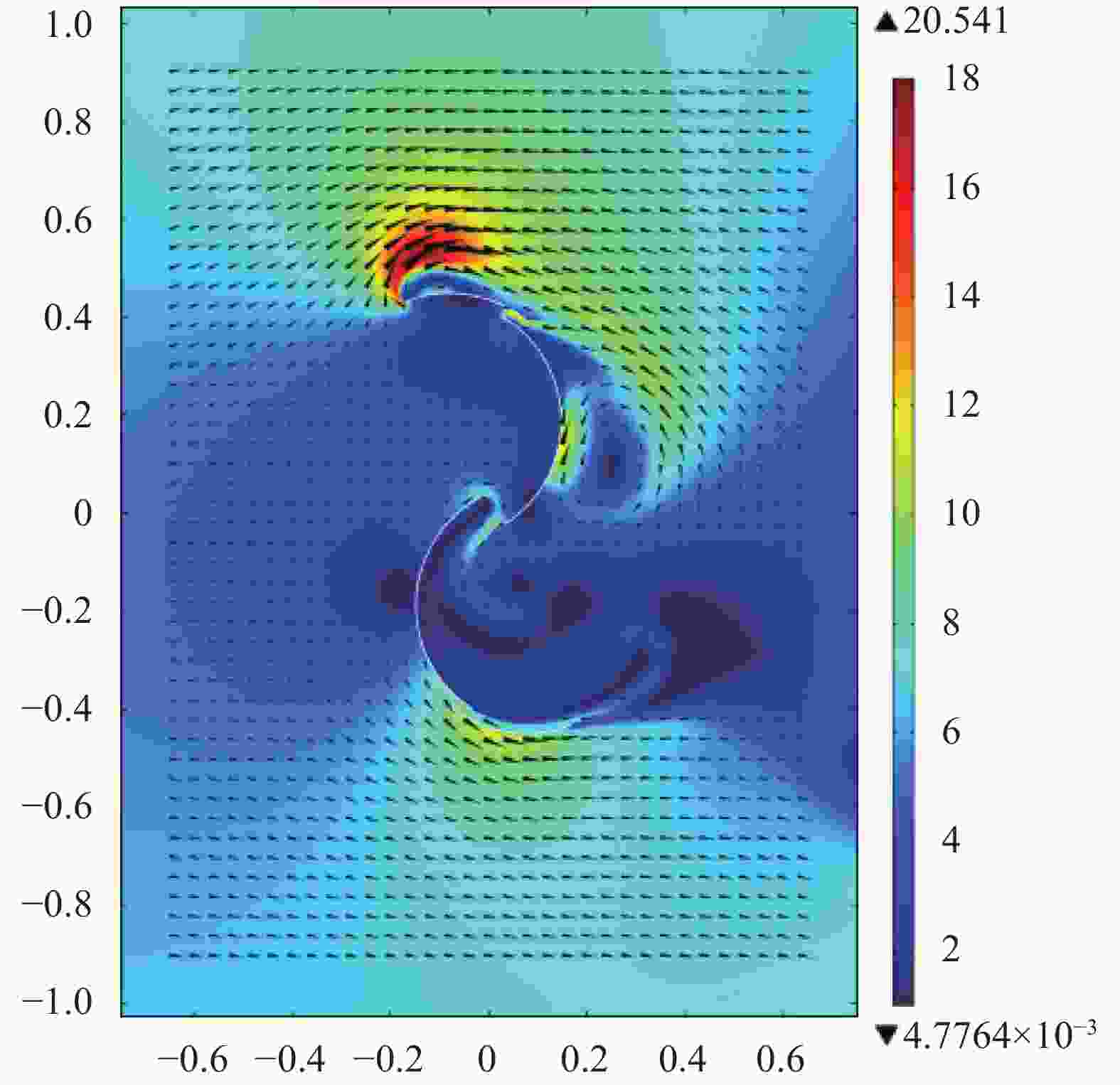
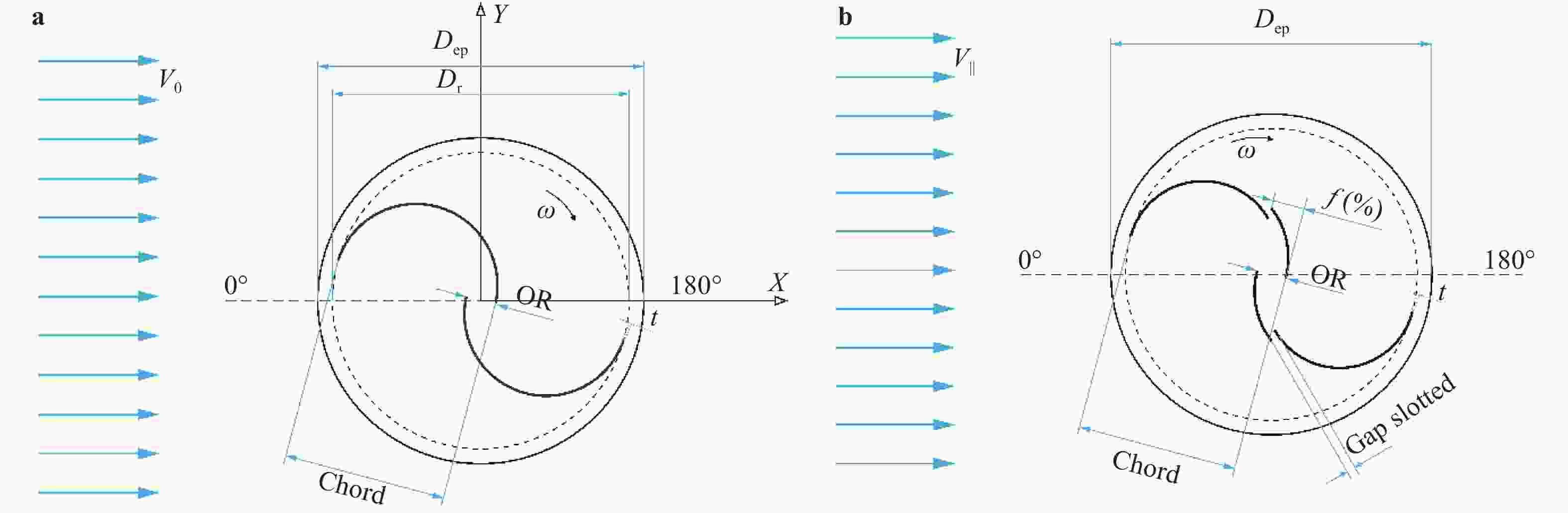
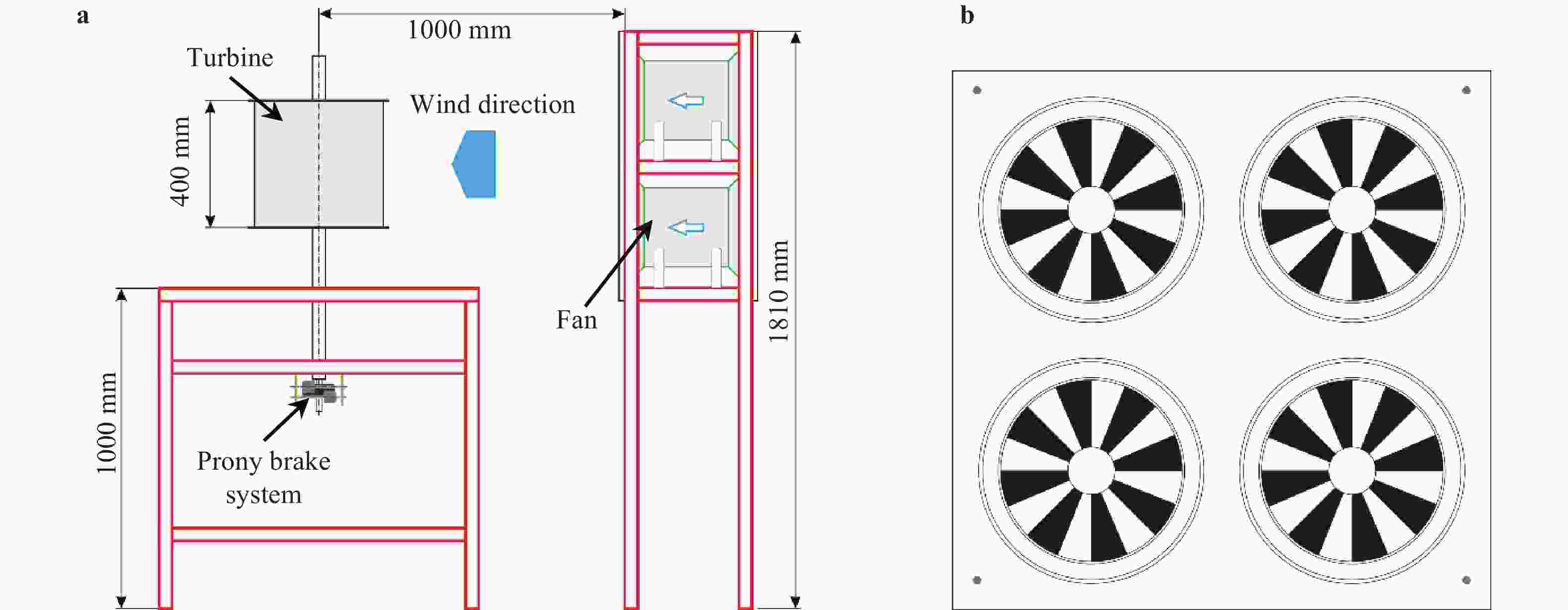
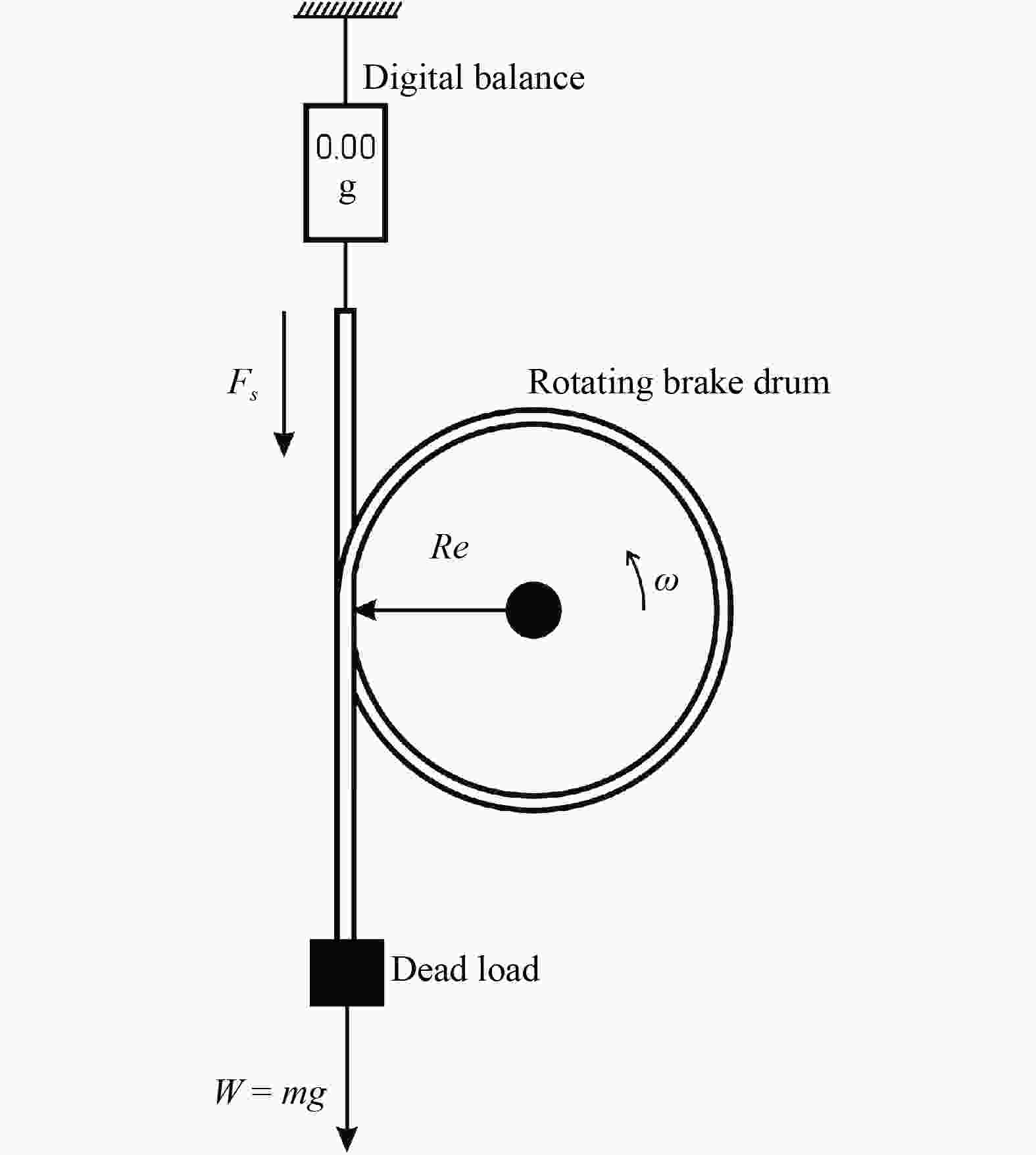
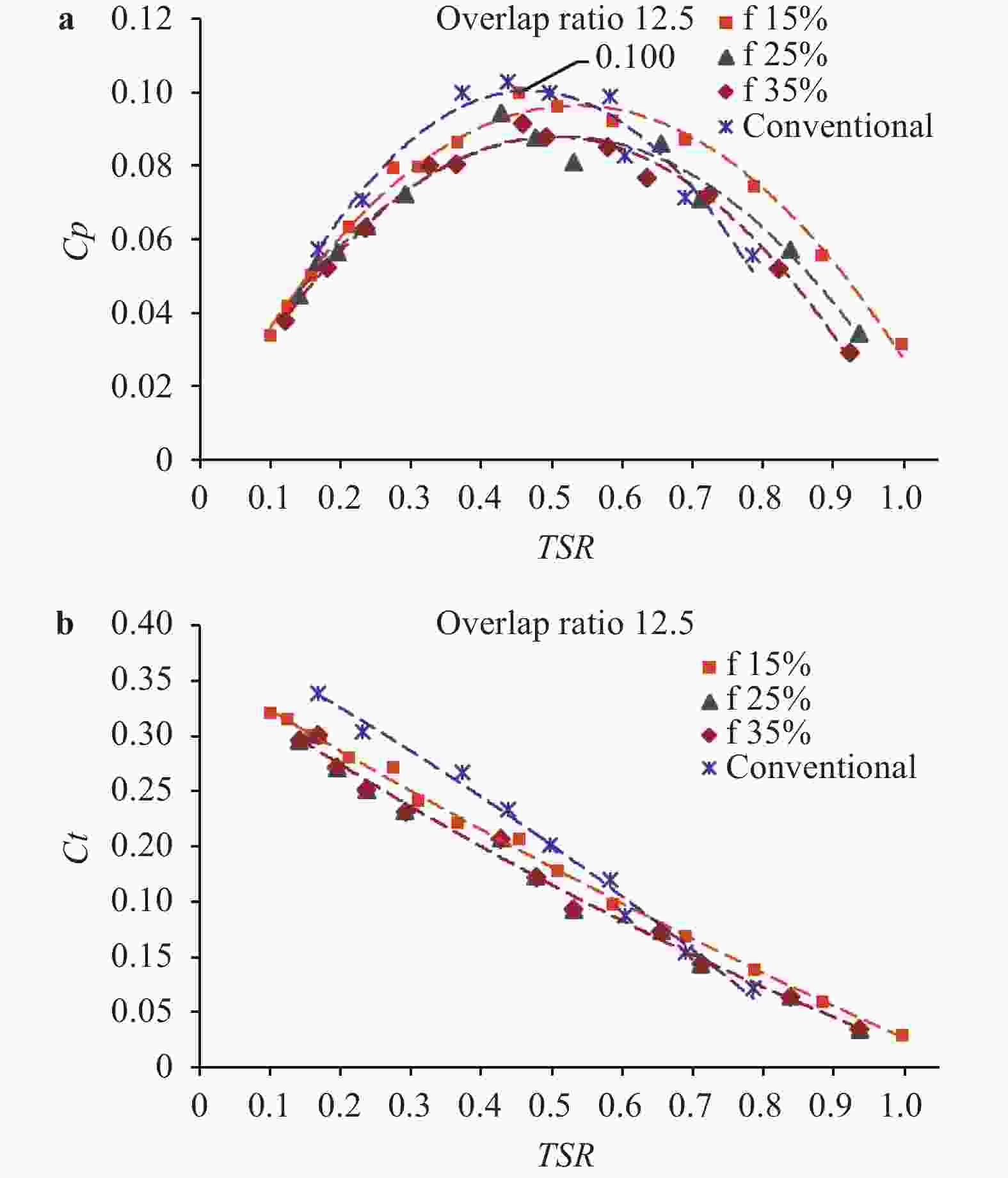
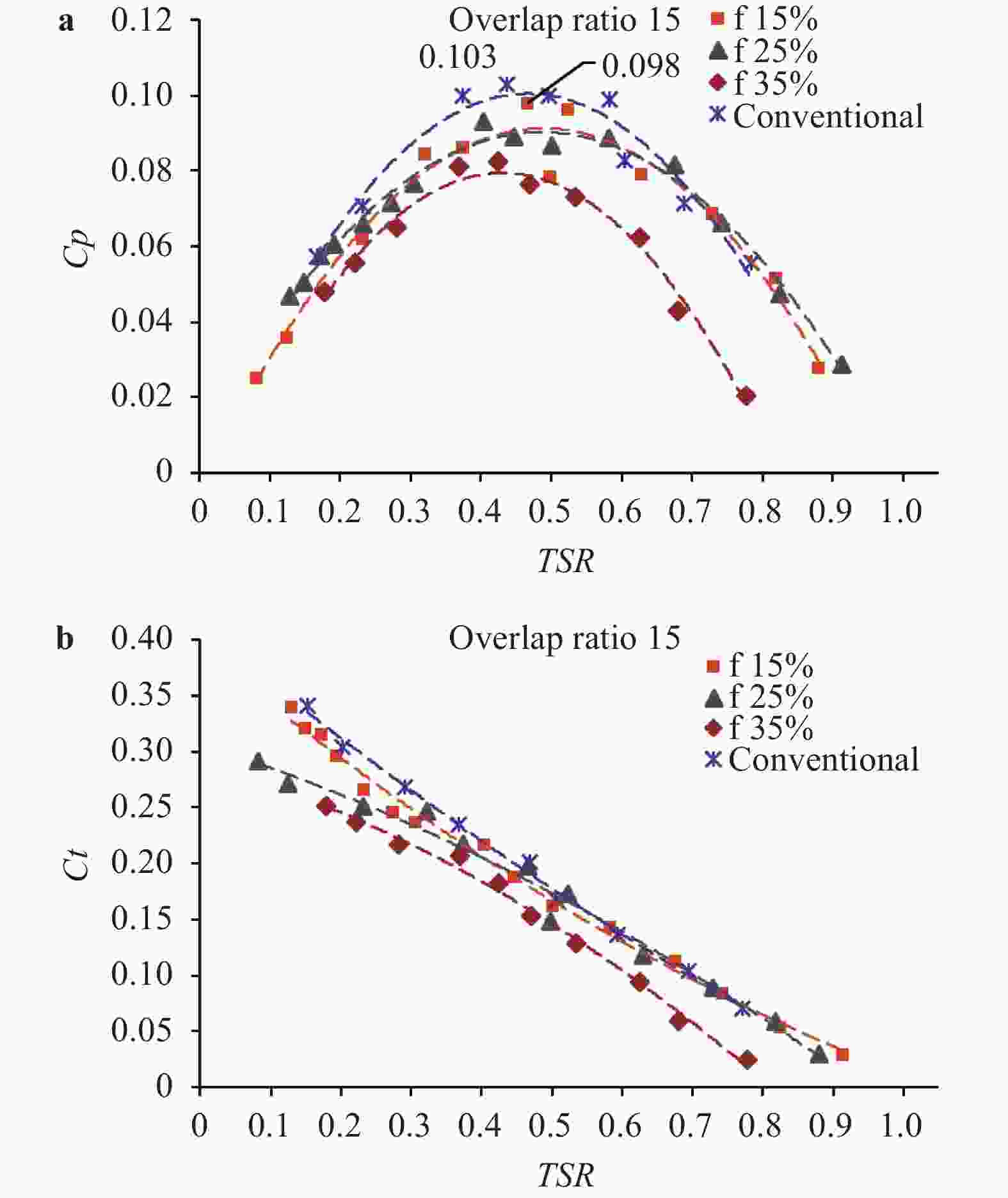
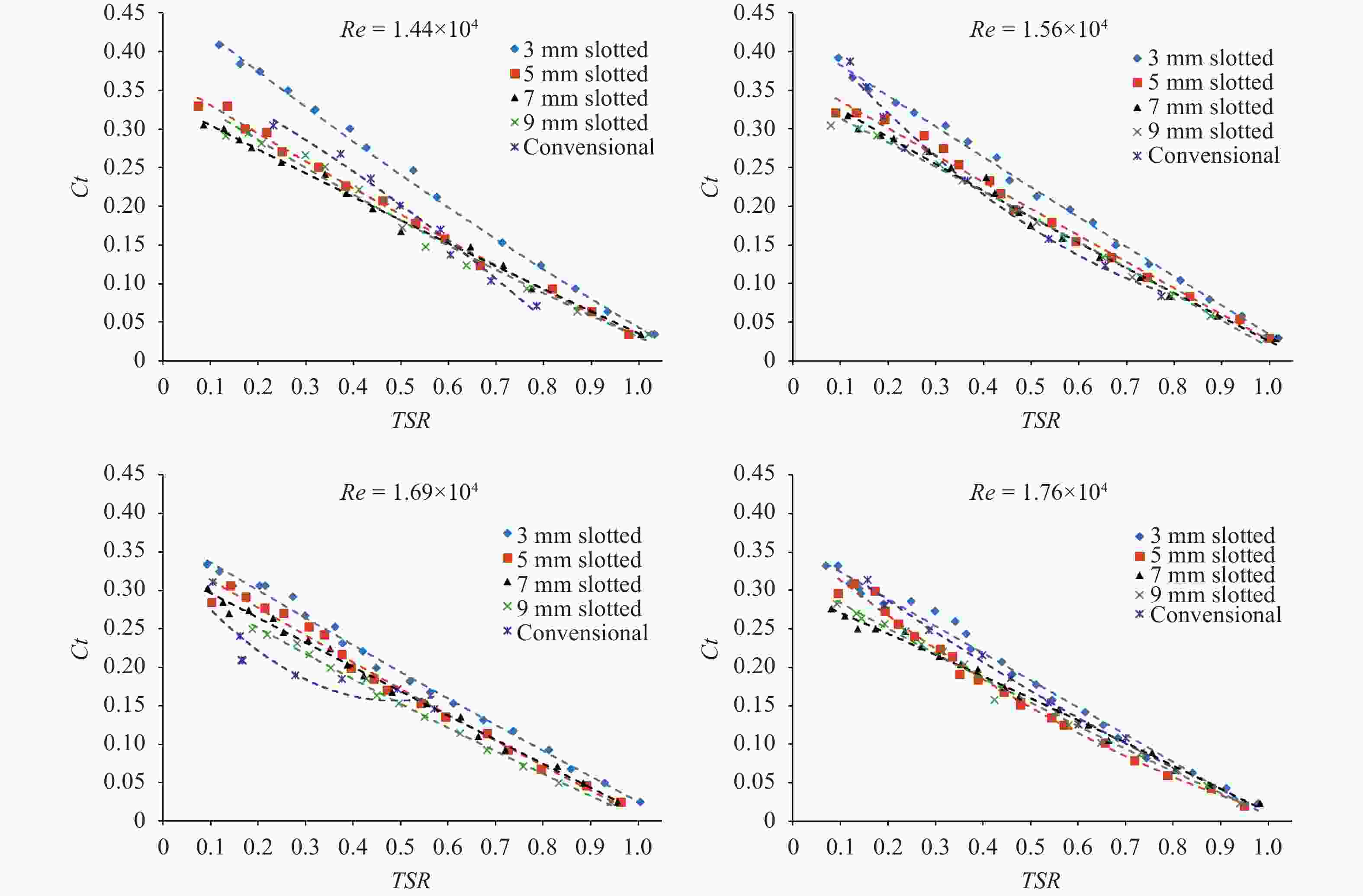
This study investigates the effect of Reynolds number on the performance of Savonius wind turbine with slotted blades. The turbine performance investigation was based on the torque coefficient (Ct), power coefficient (Cp), and tip speed ratio (TSR). The experiment used two number of blade configuration, blade overlap ratio of 10%, 12.5% and 20%, slotted position of 15%, 20%, 25% and 35%, and also slotted gap width of 3 mm, 5 mm, 7 mm, and 9 mm. The wind speed carried out in this experiment are 5.94 m/s, 6.46 m/s, 6.99 m/s, and 7.27 m/s, which are generated from the fan blowers as a wind source. The Savonius turbine with 10% overlap ratio shows the best performance. The highest Cp obtained is 0.138 by the variation of a 3 mm gap with Re of 1.44 × 104 and 0.526 tip speed ratio (TSR).
This study investigates the effect of Reynolds number on the performance of Savonius wind turbine with slotted blades. The turbine performance investigation was based on the torque coefficient (Ct), power coefficient (Cp), and tip speed ratio (TSR). The experiment used two number of blade configuration, blade overlap ratio of 10%, 12.5% and 20%, slotted position of 15%, 20%, 25% and 35%, and also slotted gap width of 3 mm, 5 mm, 7 mm, and 9 mm. The wind speed carried out in this experiment are 5.94 m/s, 6.46 m/s, 6.99 m/s, and 7.27 m/s, which are generated from the fan blowers as a wind source. The Savonius turbine with 10% overlap ratio shows the best performance. The highest Cp obtained is 0.138 by the variation of a 3 mm gap with Re of 1.44 × 104 and 0.526 tip speed ratio (TSR).
 Submit a Paper
Submit a Paper
 Subscription
Subscription
News
MORE+
Call for Papers
MORE+
- Crossing-Mechanics Driven by Big Data
- Machine learning in the fluid mechanics research of wind energy
- Mechanics of Origami/Kirigami structures and metamaterials
- New insights and perspectives on impact biomechanics for human tissues: from injury prevention, protection to protective equipment
- Environmental Mechanics for Extreme Natural Events