Institute of Mechanics,
Chinese Academy of Sciences
2020 Vol.10(3)
column
Display Mode: |
Theoretical and Applied Mechanics Letters 2020, 10(3): 141-142.
doi: 10.1016/j.taml.2020.01.041
Abstract:
Theoretical and Applied Mechanics Letters 2020, 10(3): 143-148.
doi: 10.1016/j.taml.2020.01.023
Abstract:
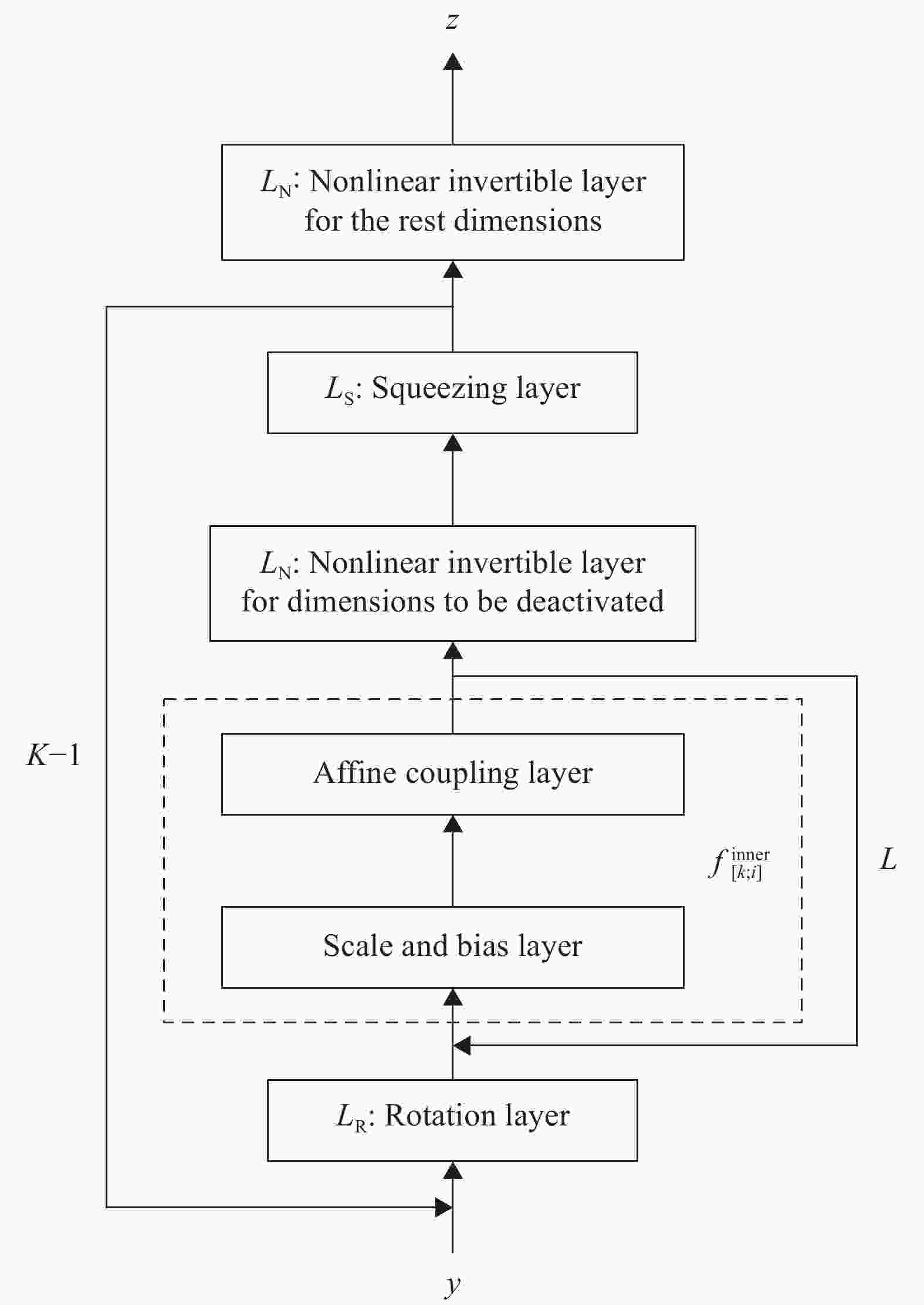
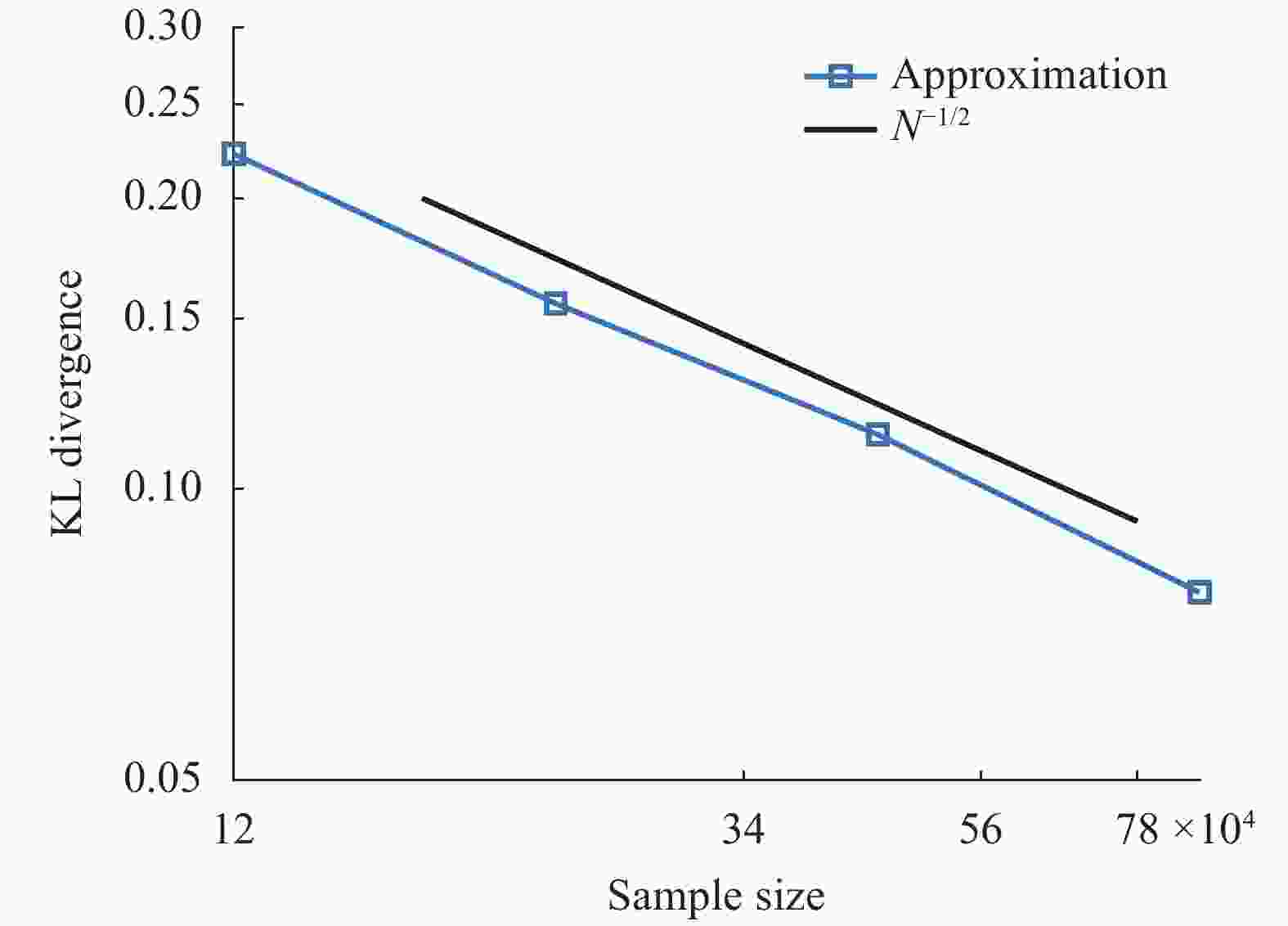
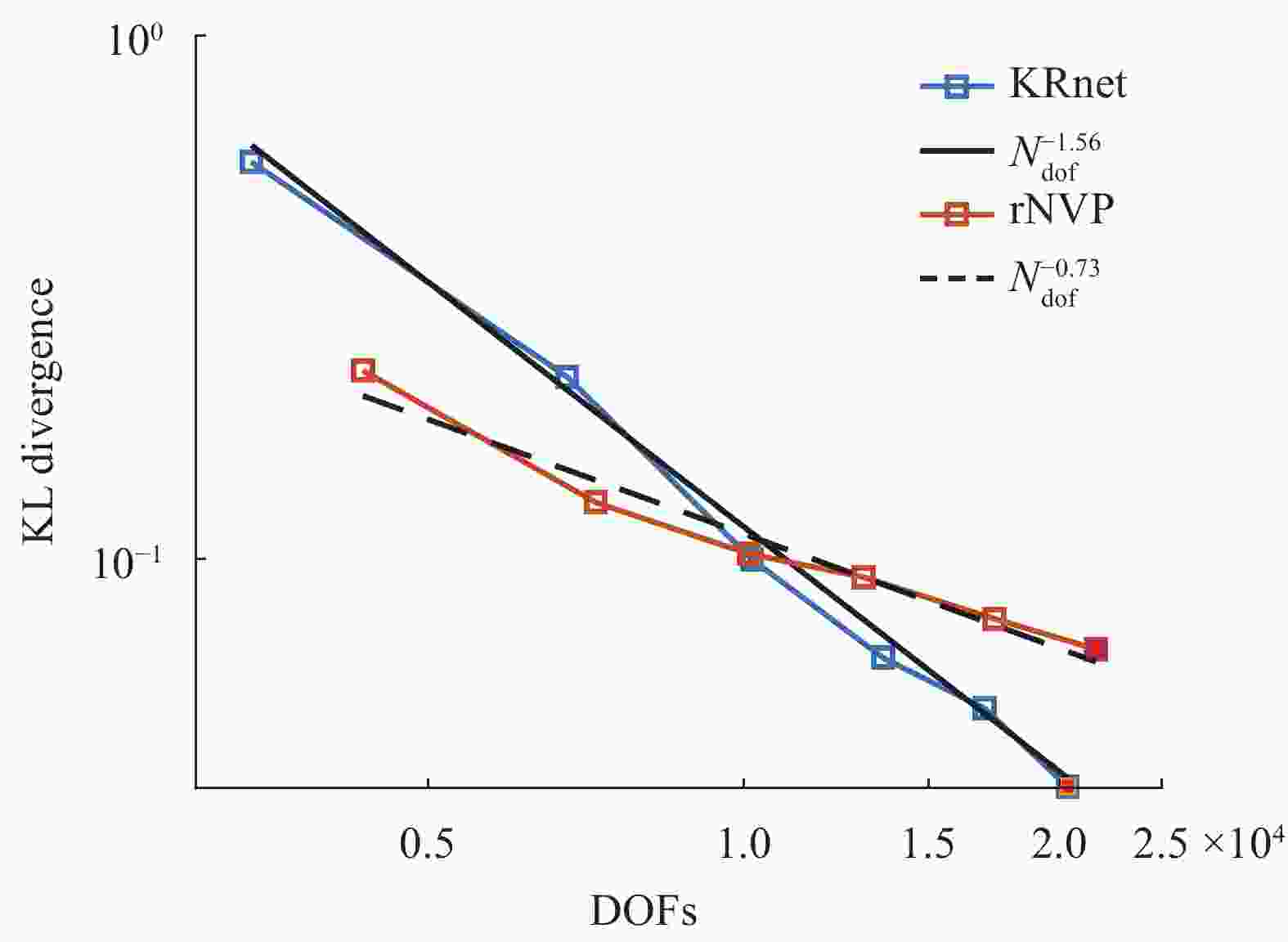
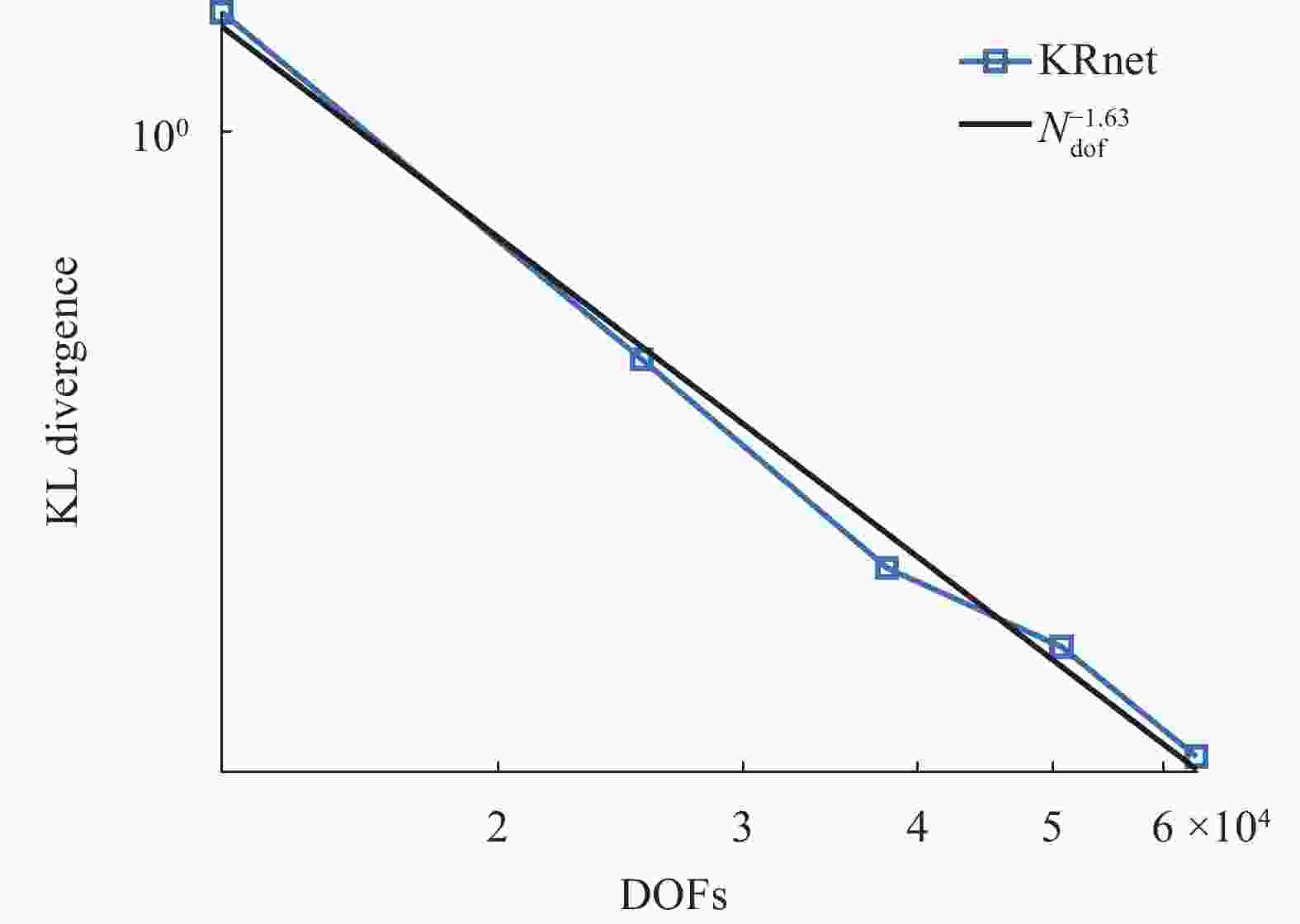
In this work, we develop an invertible transport map, called KRnet, for density estimation by coupling the Knothe–Rosenblatt (KR) rearrangement and the flow-based generative model, which generalizes the real-valued non-volume preserving (real NVP) model (arX-iv:1605.08803v3). The triangular structure of the KR rearrangement breaks the symmetry of the real NVP in terms of the exchange of information between dimensions, which not only accelerates the training process but also improves the accuracy significantly. We have also introduced several new layers into the generative model to improve both robustness and effectiveness, including a reformulated affine coupling layer, a rotation layer and a component-wise nonlinear invertible layer. The KRnet can be used for both density estimation and sample generation especially when the dimensionality is relatively high. Numerical experiments have been presented to demonstrate the performance of KRnet.
In this work, we develop an invertible transport map, called KRnet, for density estimation by coupling the Knothe–Rosenblatt (KR) rearrangement and the flow-based generative model, which generalizes the real-valued non-volume preserving (real NVP) model (arX-iv:1605.08803v3). The triangular structure of the KR rearrangement breaks the symmetry of the real NVP in terms of the exchange of information between dimensions, which not only accelerates the training process but also improves the accuracy significantly. We have also introduced several new layers into the generative model to improve both robustness and effectiveness, including a reformulated affine coupling layer, a rotation layer and a component-wise nonlinear invertible layer. The KRnet can be used for both density estimation and sample generation especially when the dimensionality is relatively high. Numerical experiments have been presented to demonstrate the performance of KRnet.
Theoretical and Applied Mechanics Letters 2020, 10(3): 149-154.
doi: 10.1016/j.taml.2020.01.010
Abstract:
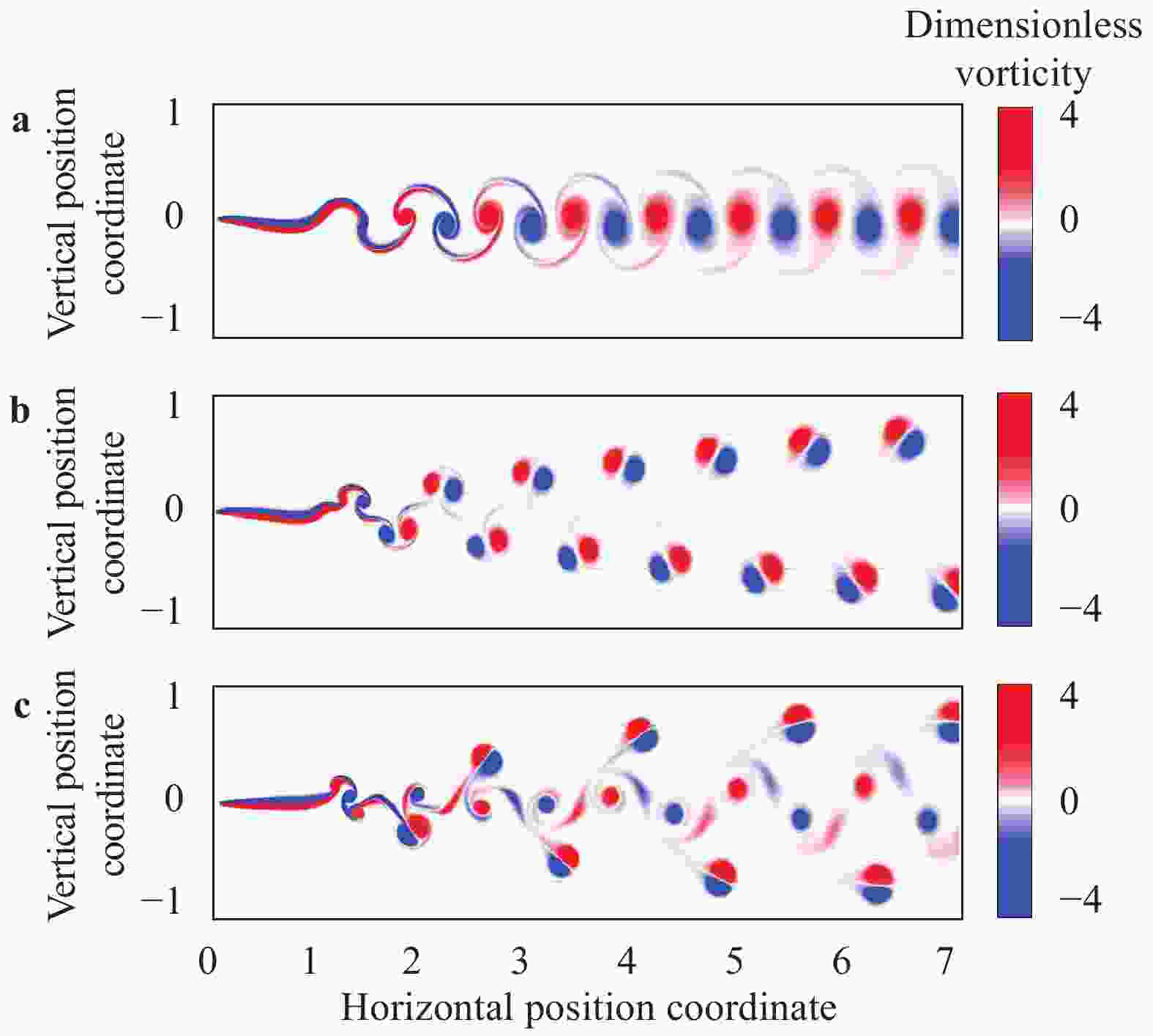
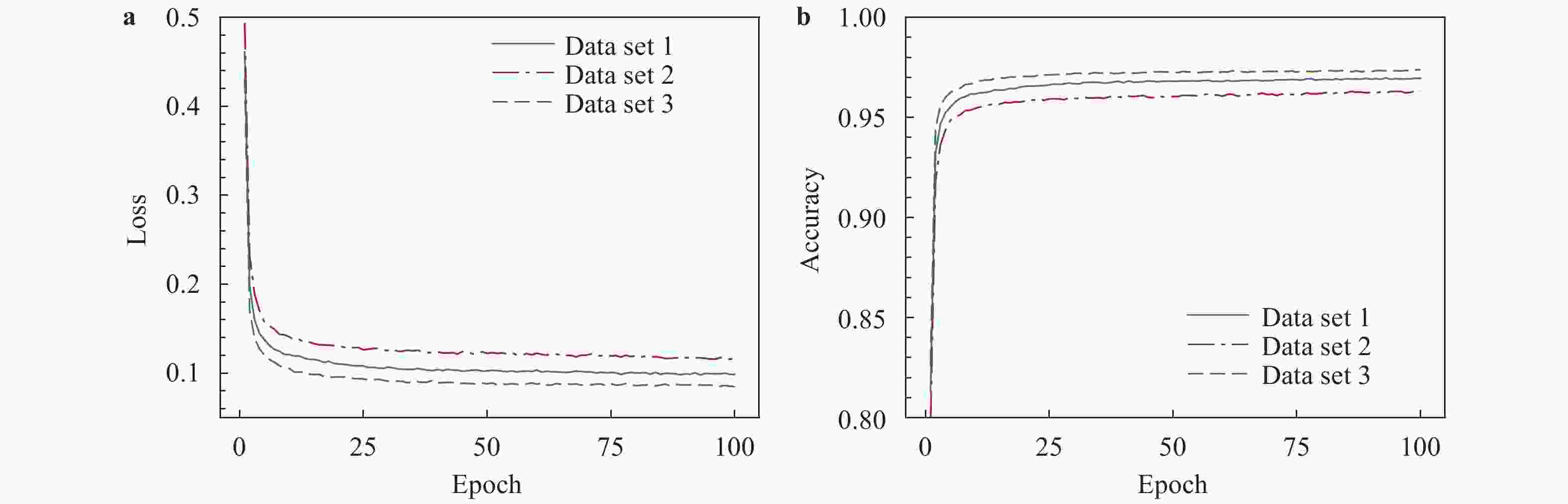
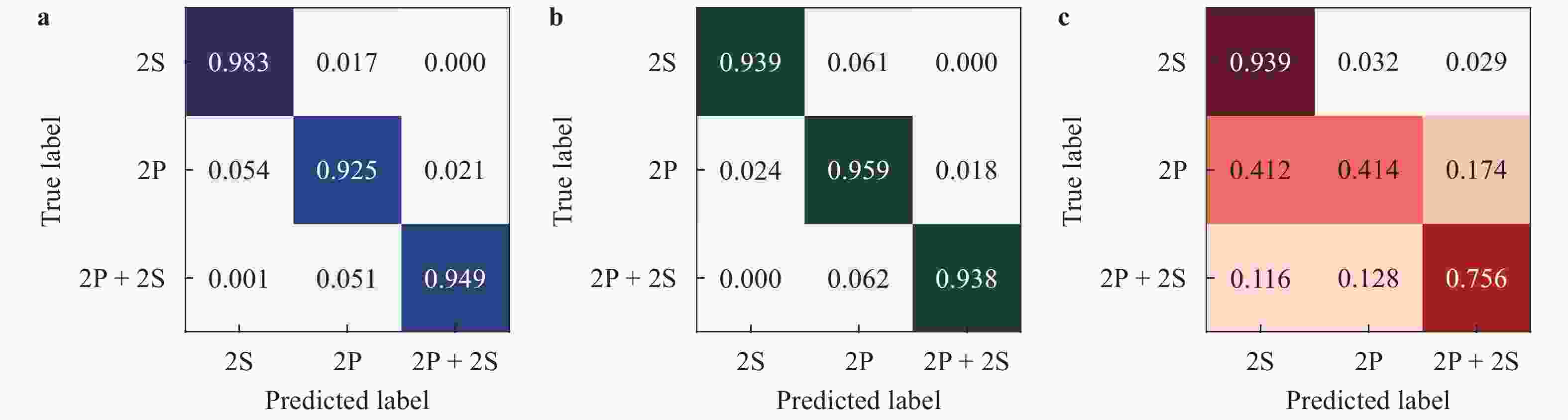
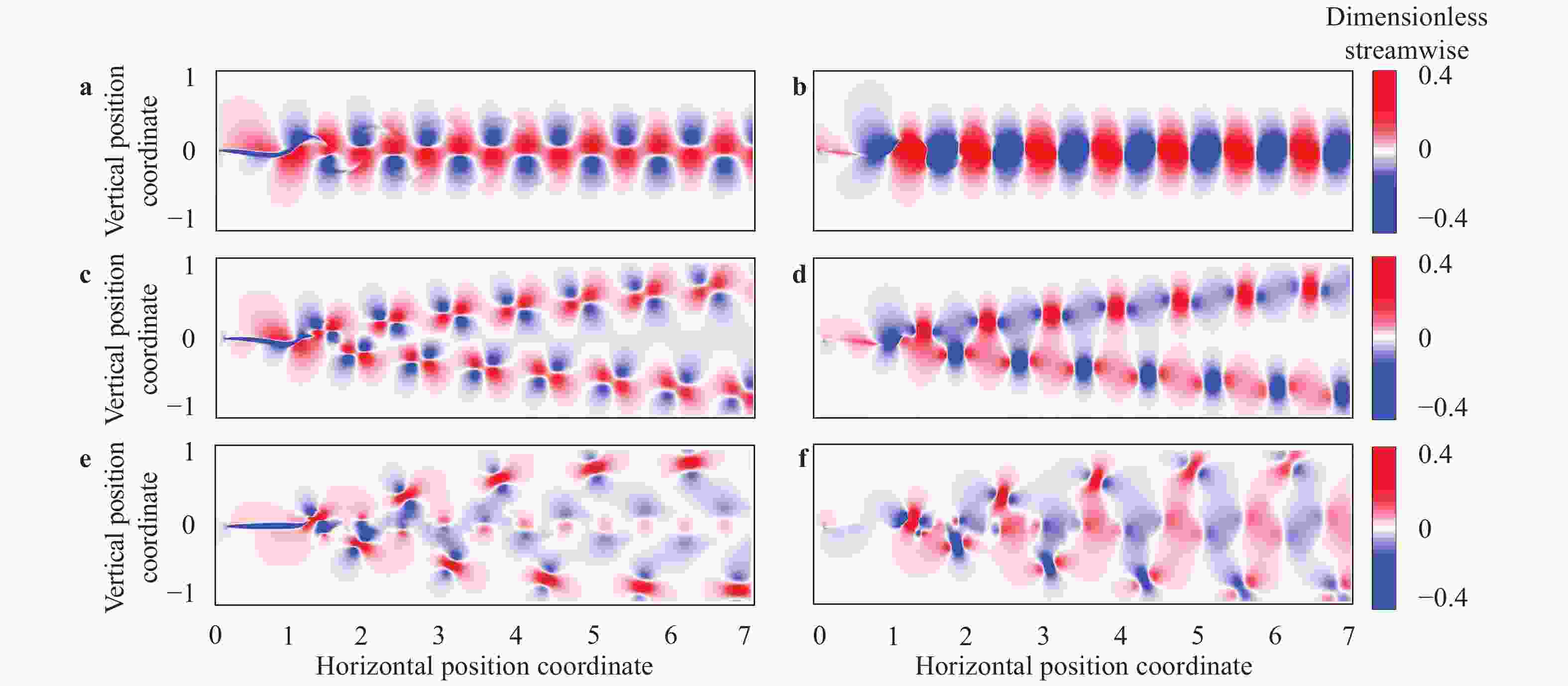
We consider the classification of wake structures produced by self-propelled fish-like swimmers based on local measurements of flow variables. This problem is inspired by the extraordinary capability of animal swimmers in perceiving their hydrodynamic environments under dark condition. We train different neural networks to classify wake structures by using the streamwise velocity component, the crosswise velocity component, the vorticity and the combination of three flow variables, respectively. It is found that the neural networks trained using the two velocity components perform well in identifying the wake types, whereas the neural network trained using the vorticity suffers from a high rate of misclassification. When the neural network is trained using the combination of all three flow variables, a remarkably high accuracy in wake classification can be achieved. The results of this study can be helpful to the design of flow sensory systems in robotic underwater vehicles.
We consider the classification of wake structures produced by self-propelled fish-like swimmers based on local measurements of flow variables. This problem is inspired by the extraordinary capability of animal swimmers in perceiving their hydrodynamic environments under dark condition. We train different neural networks to classify wake structures by using the streamwise velocity component, the crosswise velocity component, the vorticity and the combination of three flow variables, respectively. It is found that the neural networks trained using the two velocity components perform well in identifying the wake types, whereas the neural network trained using the vorticity suffers from a high rate of misclassification. When the neural network is trained using the combination of all three flow variables, a remarkably high accuracy in wake classification can be achieved. The results of this study can be helpful to the design of flow sensory systems in robotic underwater vehicles.
Theoretical and Applied Mechanics Letters 2020, 10(3): 155-160.
doi: 10.1016/j.taml.2020.01.019
Abstract:
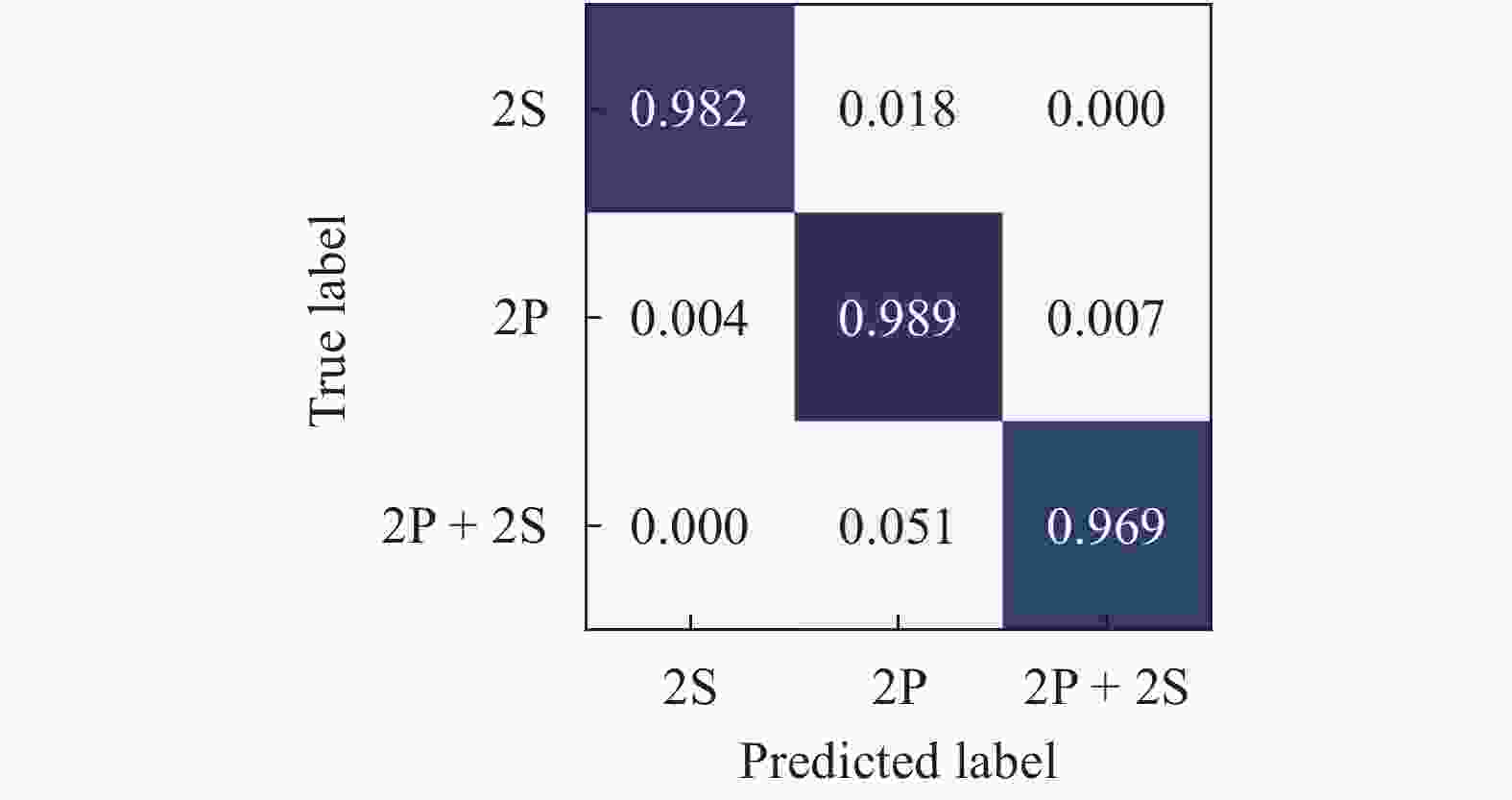
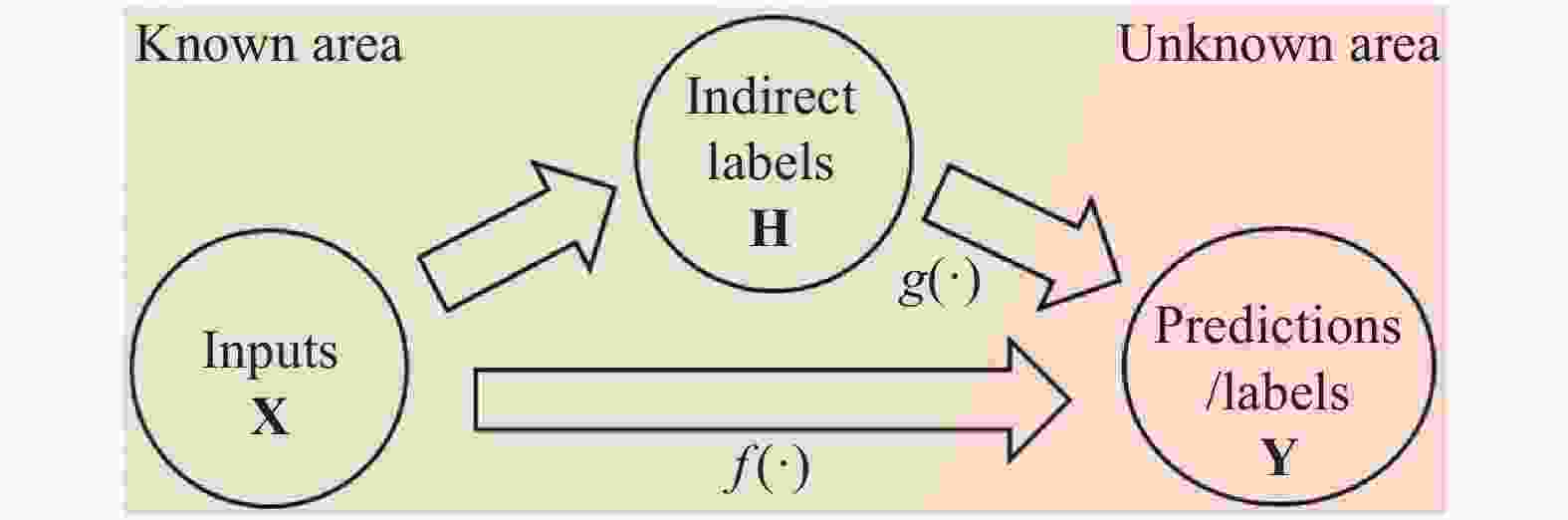
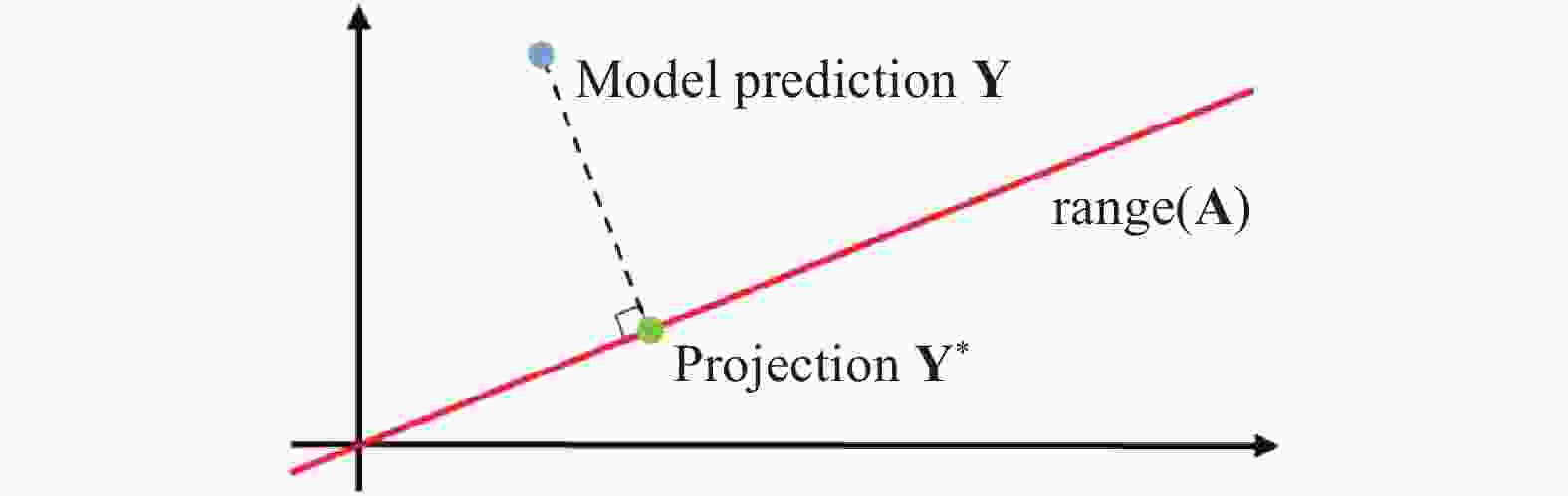
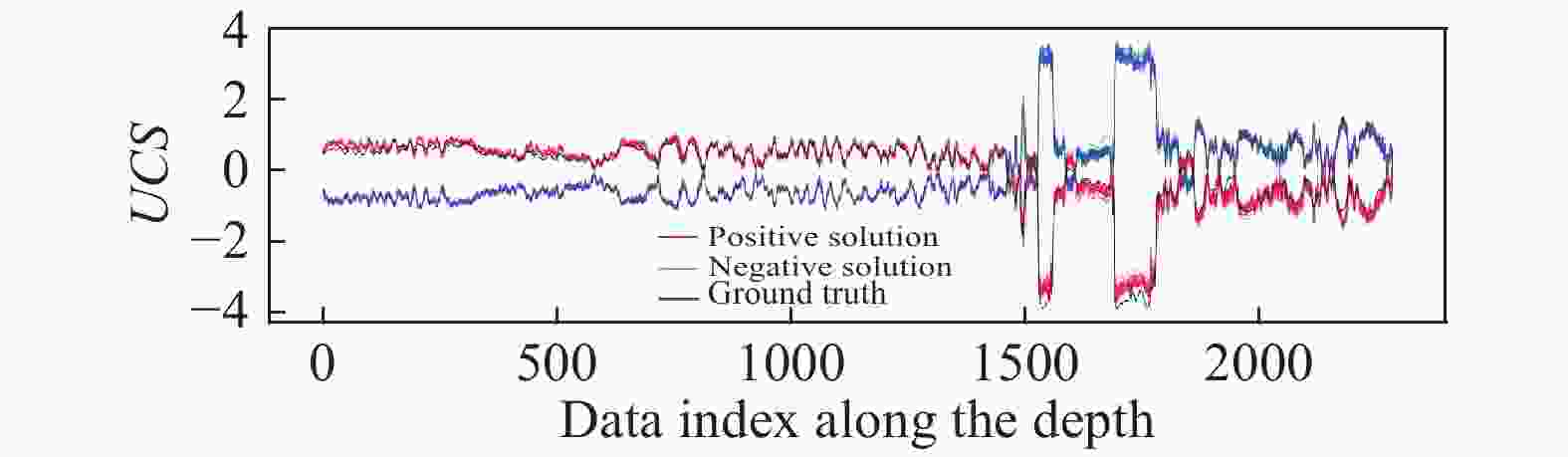
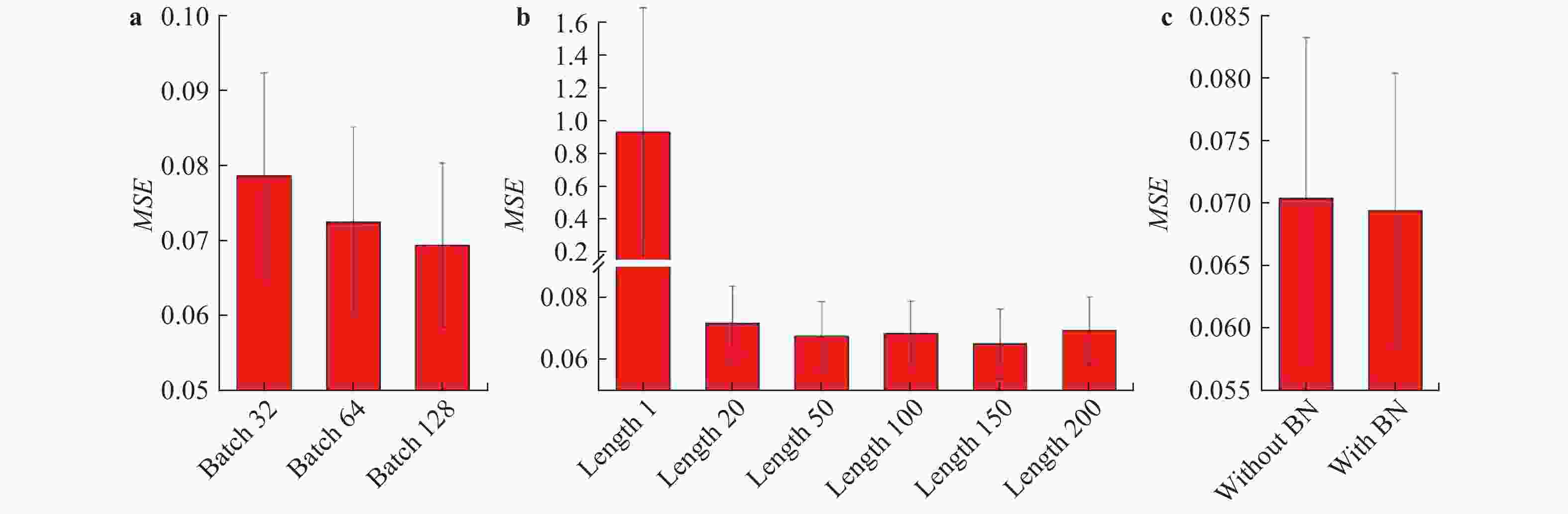
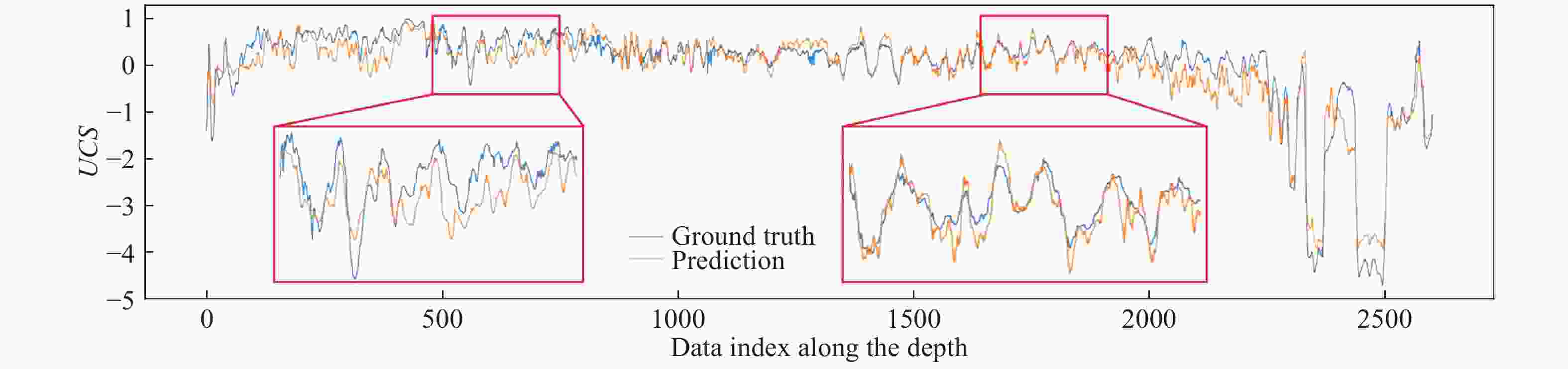
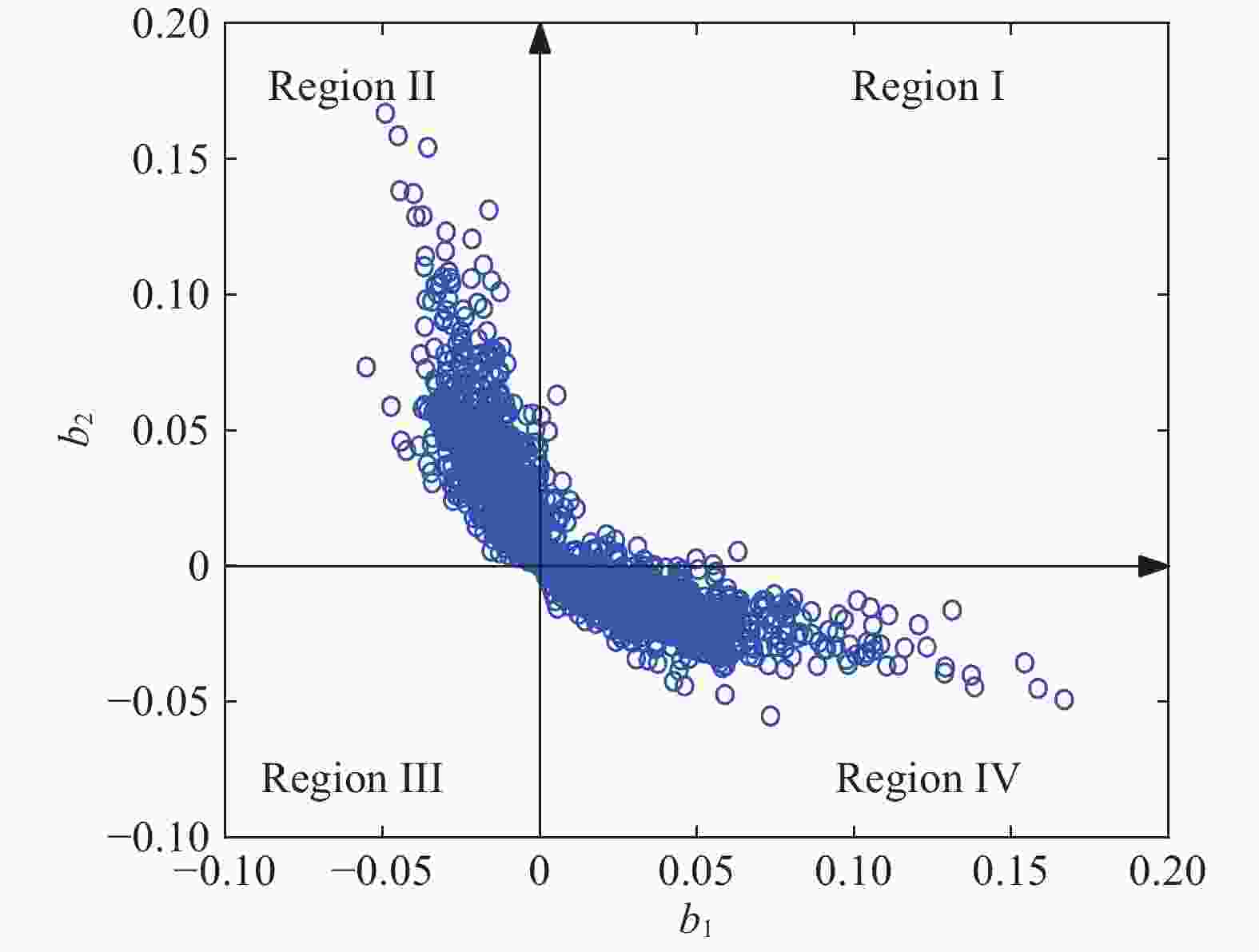
This study proposes a supervised learning method that does not rely on labels. We use variables associated with the label as indirect labels, and construct an indirect physics-constrained loss based on the physical mechanism to train the model. In the training process, the model prediction is mapped to the space of value that conforms to the physical mechanism through the projection matrix, and then the model is trained based on the indirect labels. The final prediction result of the model conforms to the physical mechanism between indirect label and label, and also meets the constraints of the indirect label. The present study also develops projection matrix normalization and prediction covariance analysis to ensure that the model can be fully trained. Finally, the effect of the physics-constrained indirect supervised learning is verified based on a well log generation problem.
This study proposes a supervised learning method that does not rely on labels. We use variables associated with the label as indirect labels, and construct an indirect physics-constrained loss based on the physical mechanism to train the model. In the training process, the model prediction is mapped to the space of value that conforms to the physical mechanism through the projection matrix, and then the model is trained based on the indirect labels. The final prediction result of the model conforms to the physical mechanism between indirect label and label, and also meets the constraints of the indirect label. The present study also develops projection matrix normalization and prediction covariance analysis to ensure that the model can be fully trained. Finally, the effect of the physics-constrained indirect supervised learning is verified based on a well log generation problem.
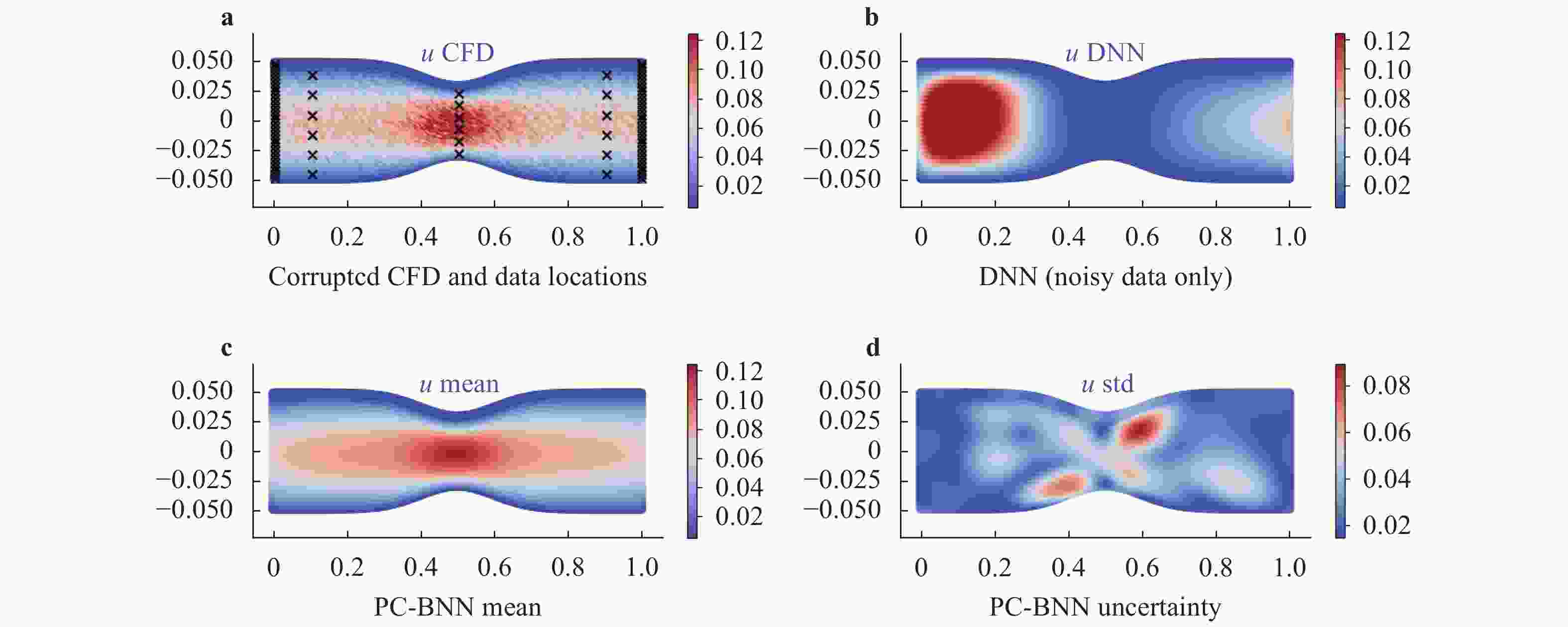
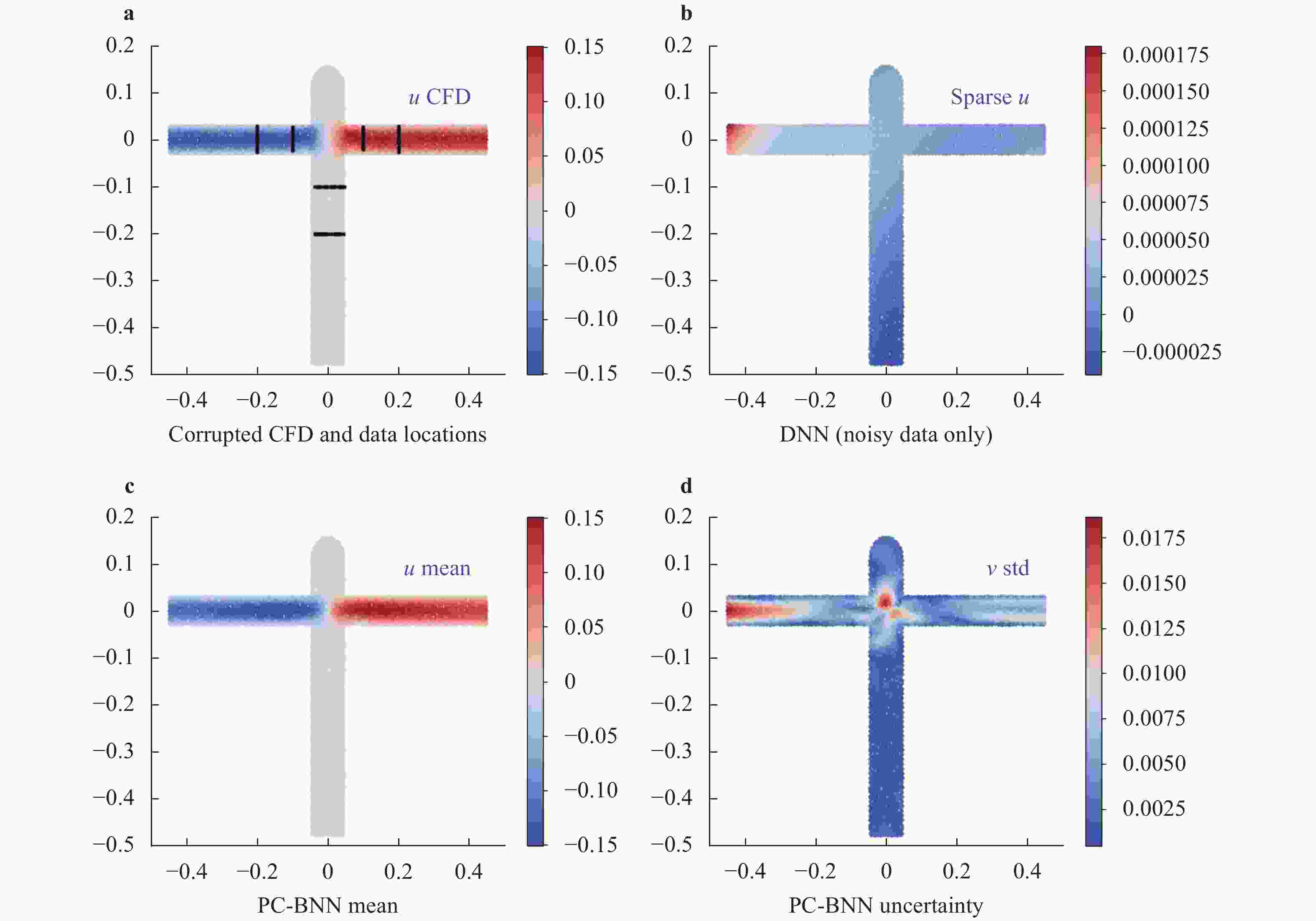
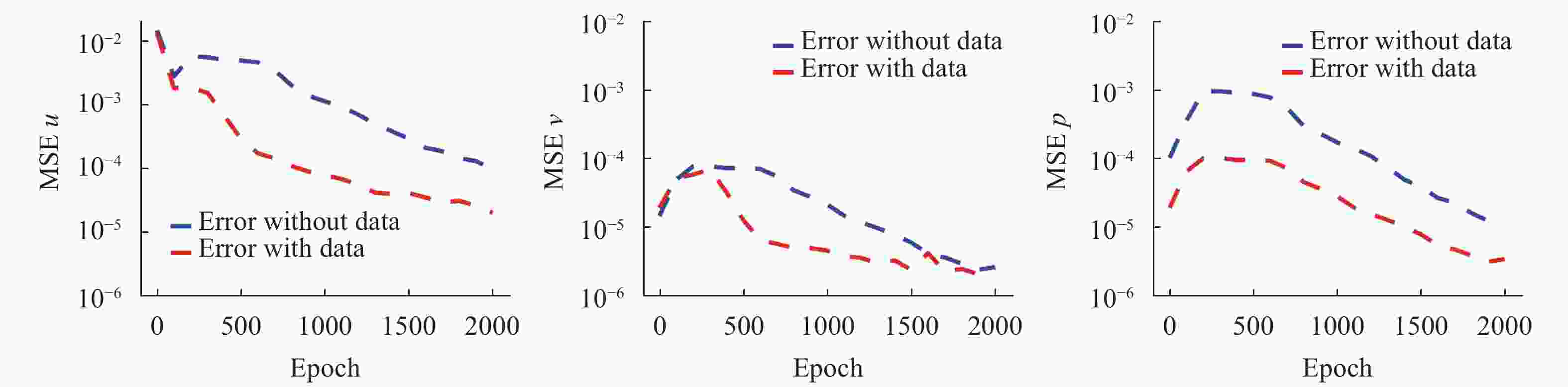
Physics-constrained bayesian neural network for fluid flow reconstruction with sparse and noisy data
Theoretical and Applied Mechanics Letters 2020, 10(3): 161-169.
doi: 10.1016/j.taml.2020.01.031
Abstract:
In many applications, flow measurements are usually sparse and possibly noisy. The reconstruction of a high-resolution flow field from limited and imperfect flow information is significant yet challenging. In this work, we propose an innovative physics-constrained Bayesian deep learning approach to reconstruct flow fields from sparse, noisy velocity data, where equation-based constraints are imposed through the likelihood function and uncertainty of the reconstructed flow can be estimated. Specifically, a Bayesian deep neural network is trained on sparse measurement data to capture the flow field. In the meantime, the violation of physical laws will be penalized on a large number of spatiotemporal points where measurements are not available. A non-parametric variational inference approach is applied to enable efficient physics-constrained Bayesian learning. Several test cases on idealized vascular flows with synthetic measurement data are studied to demonstrate the merit of the proposed method.
In many applications, flow measurements are usually sparse and possibly noisy. The reconstruction of a high-resolution flow field from limited and imperfect flow information is significant yet challenging. In this work, we propose an innovative physics-constrained Bayesian deep learning approach to reconstruct flow fields from sparse, noisy velocity data, where equation-based constraints are imposed through the likelihood function and uncertainty of the reconstructed flow can be estimated. Specifically, a Bayesian deep neural network is trained on sparse measurement data to capture the flow field. In the meantime, the violation of physical laws will be penalized on a large number of spatiotemporal points where measurements are not available. A non-parametric variational inference approach is applied to enable efficient physics-constrained Bayesian learning. Several test cases on idealized vascular flows with synthetic measurement data are studied to demonstrate the merit of the proposed method.
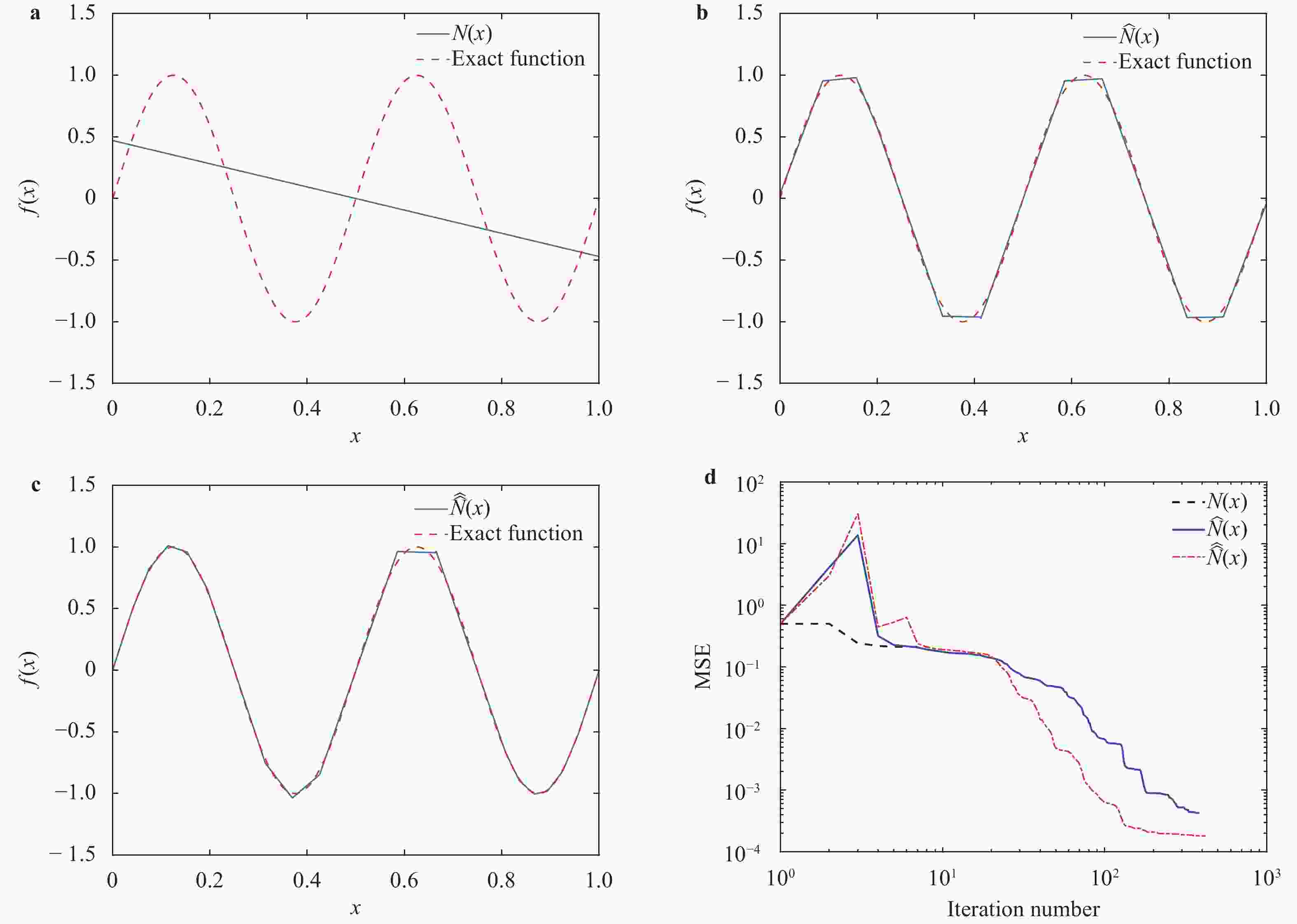
Theoretical and Applied Mechanics Letters 2020, 10(3): 170-181.
doi: 10.1016/j.taml.2020.01.043
Abstract:
For neural networks (NNs) with rectified linear unit (ReLU) or binary activation functions, we show that their training can be accomplished in a reduced parameter space. Specifically, the weights in each neuron can be trained on the unit sphere, as opposed to the entire space, and the threshold can be trained in a bounded interval, as opposed to the real line. We show that the NNs in the reduced parameter space are mathematically equivalent to the standard NNs with parameters in the whole space. The reduced parameter space shall facilitate the optimization procedure for the network training, as the search space becomes (much) smaller. We demonstrate the improved training performance using numerical examples.
For neural networks (NNs) with rectified linear unit (ReLU) or binary activation functions, we show that their training can be accomplished in a reduced parameter space. Specifically, the weights in each neuron can be trained on the unit sphere, as opposed to the entire space, and the threshold can be trained in a bounded interval, as opposed to the real line. We show that the NNs in the reduced parameter space are mathematically equivalent to the standard NNs with parameters in the whole space. The reduced parameter space shall facilitate the optimization procedure for the network training, as the search space becomes (much) smaller. We demonstrate the improved training performance using numerical examples.
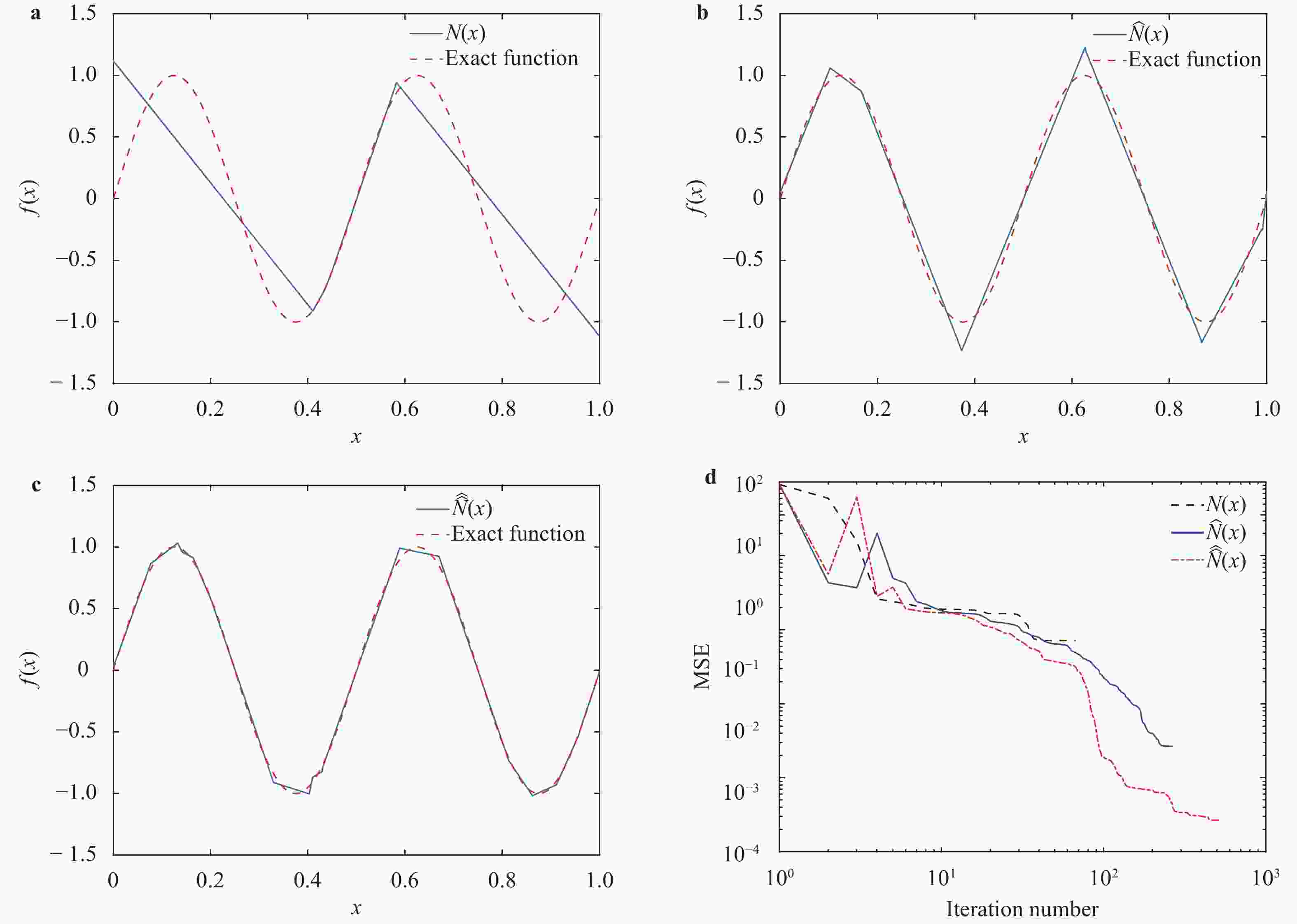
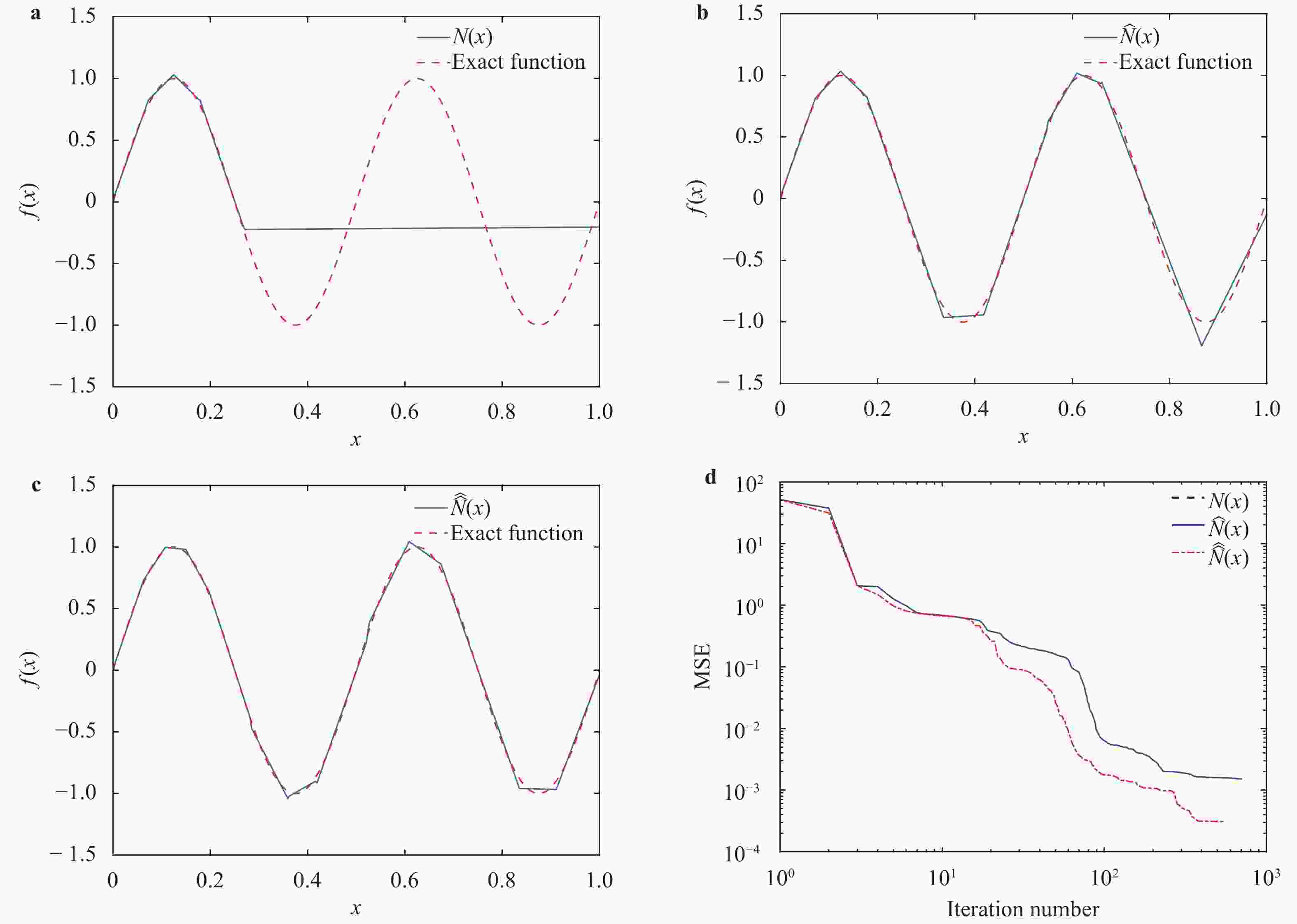
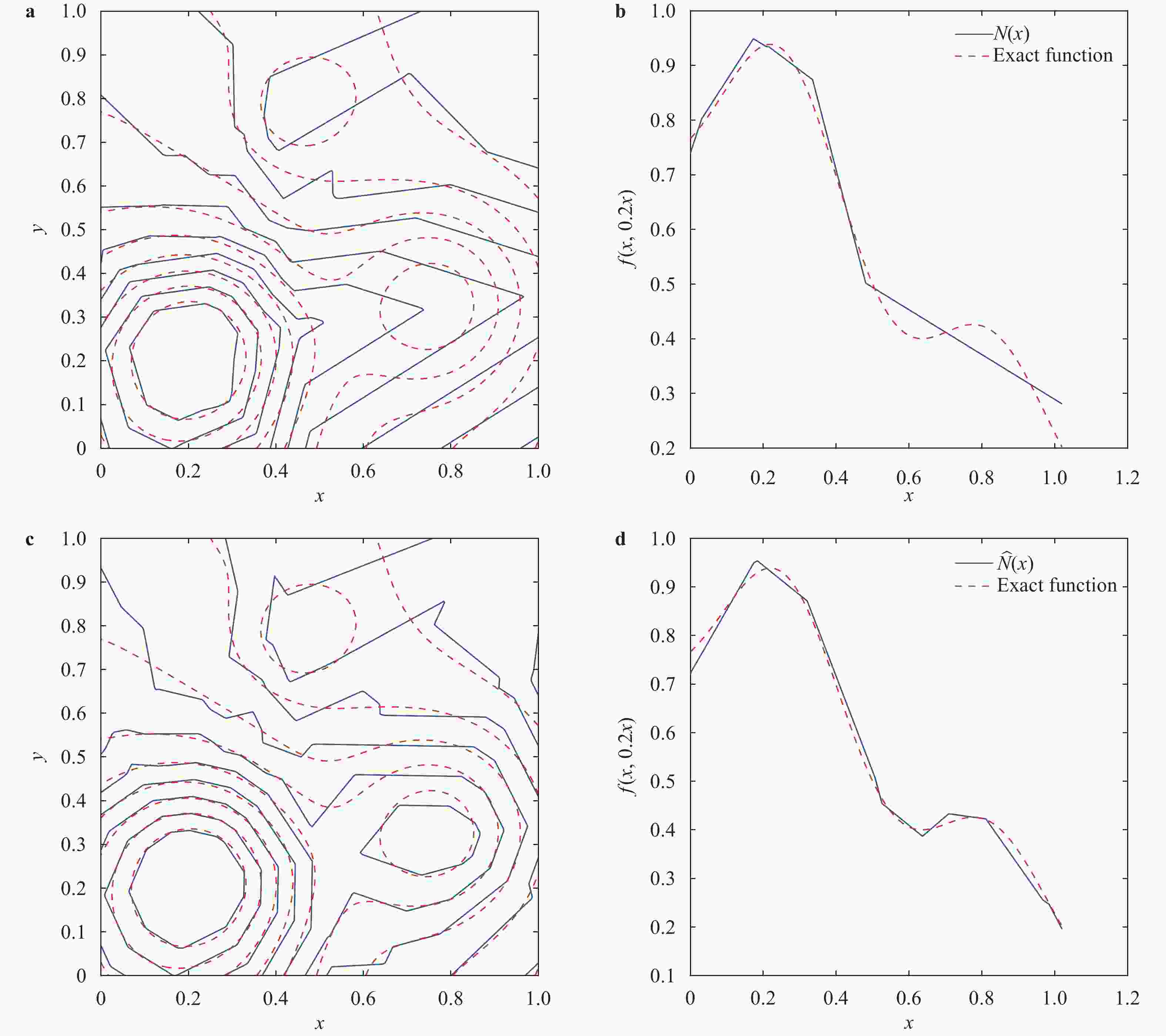
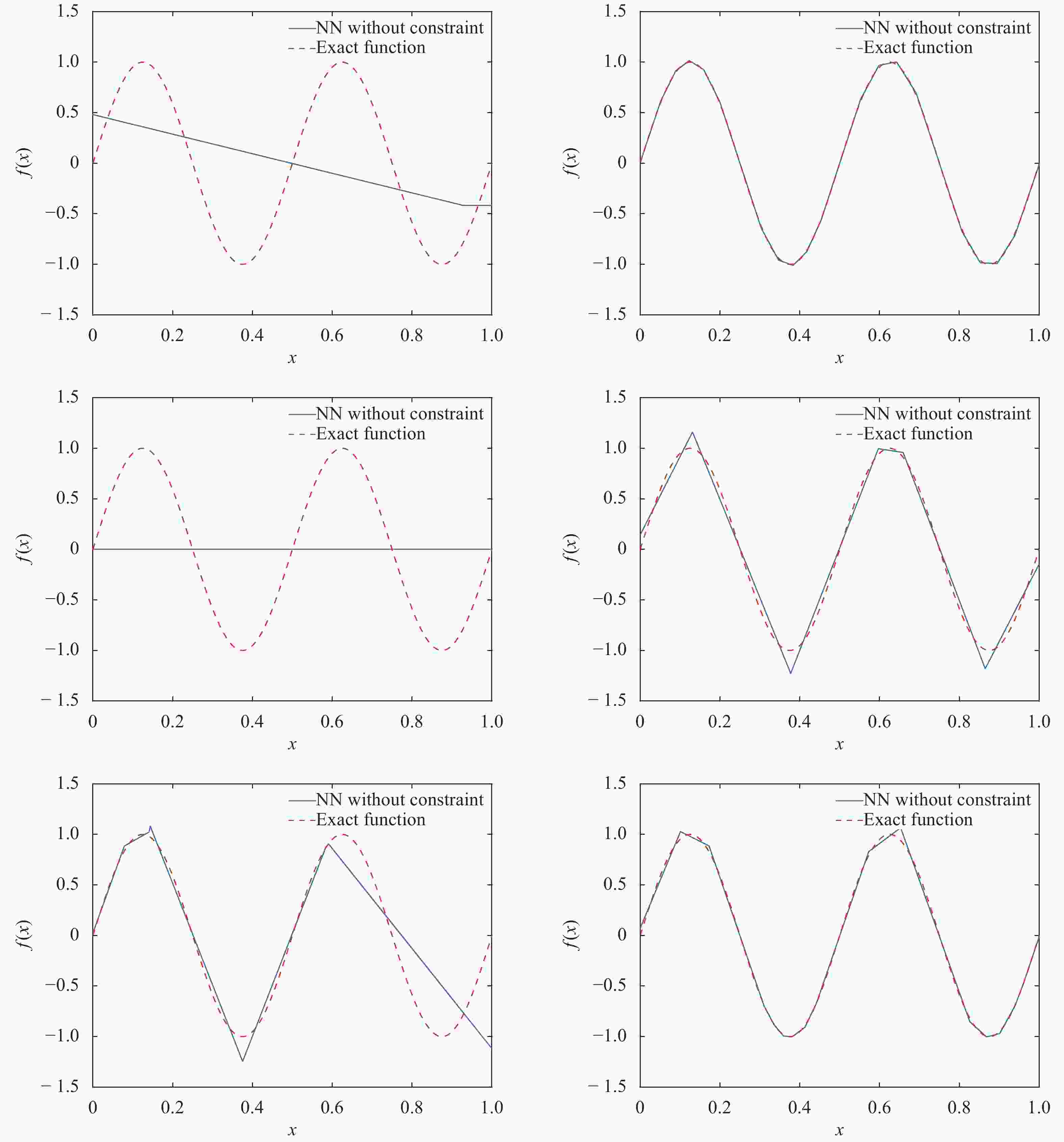
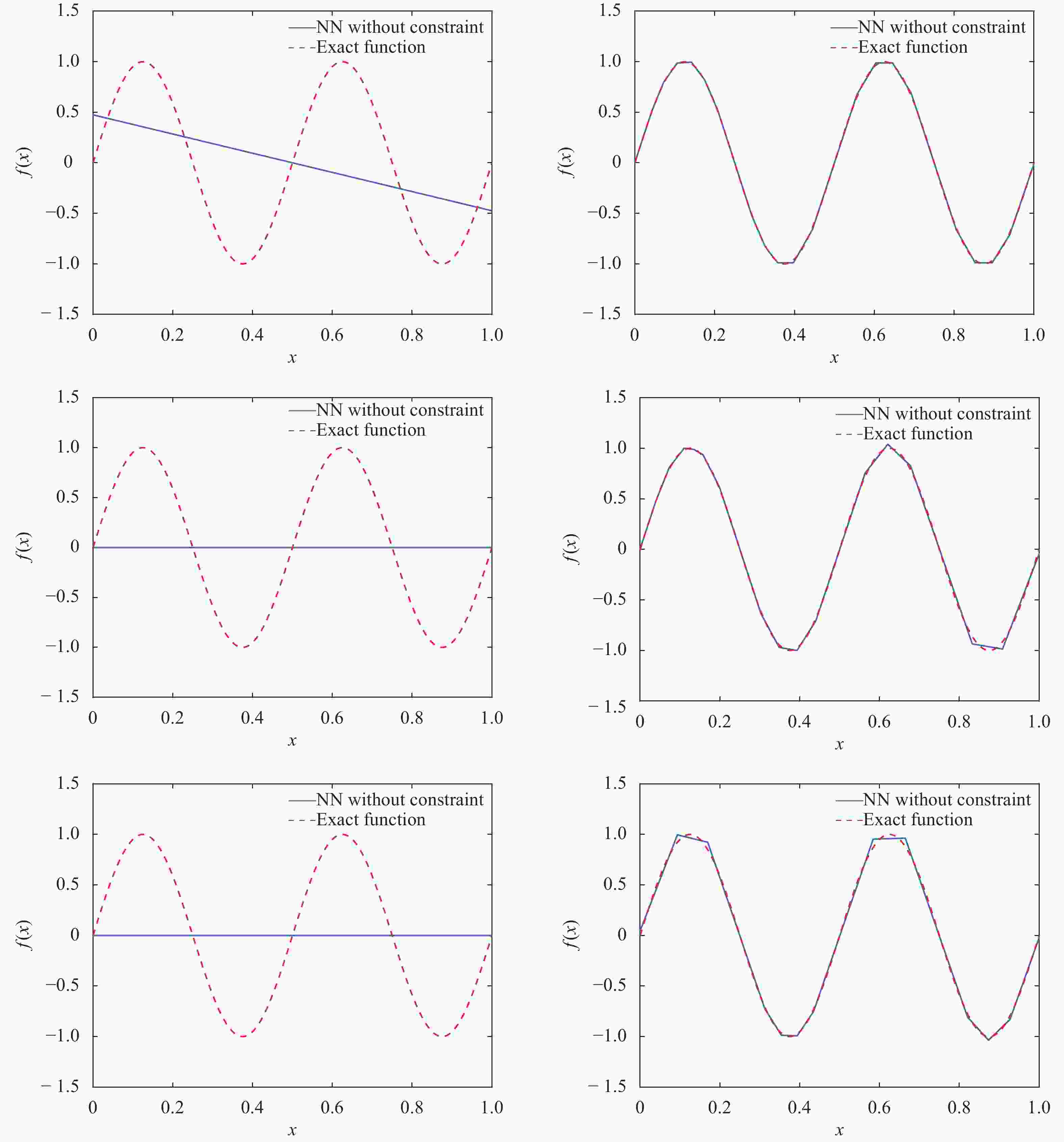
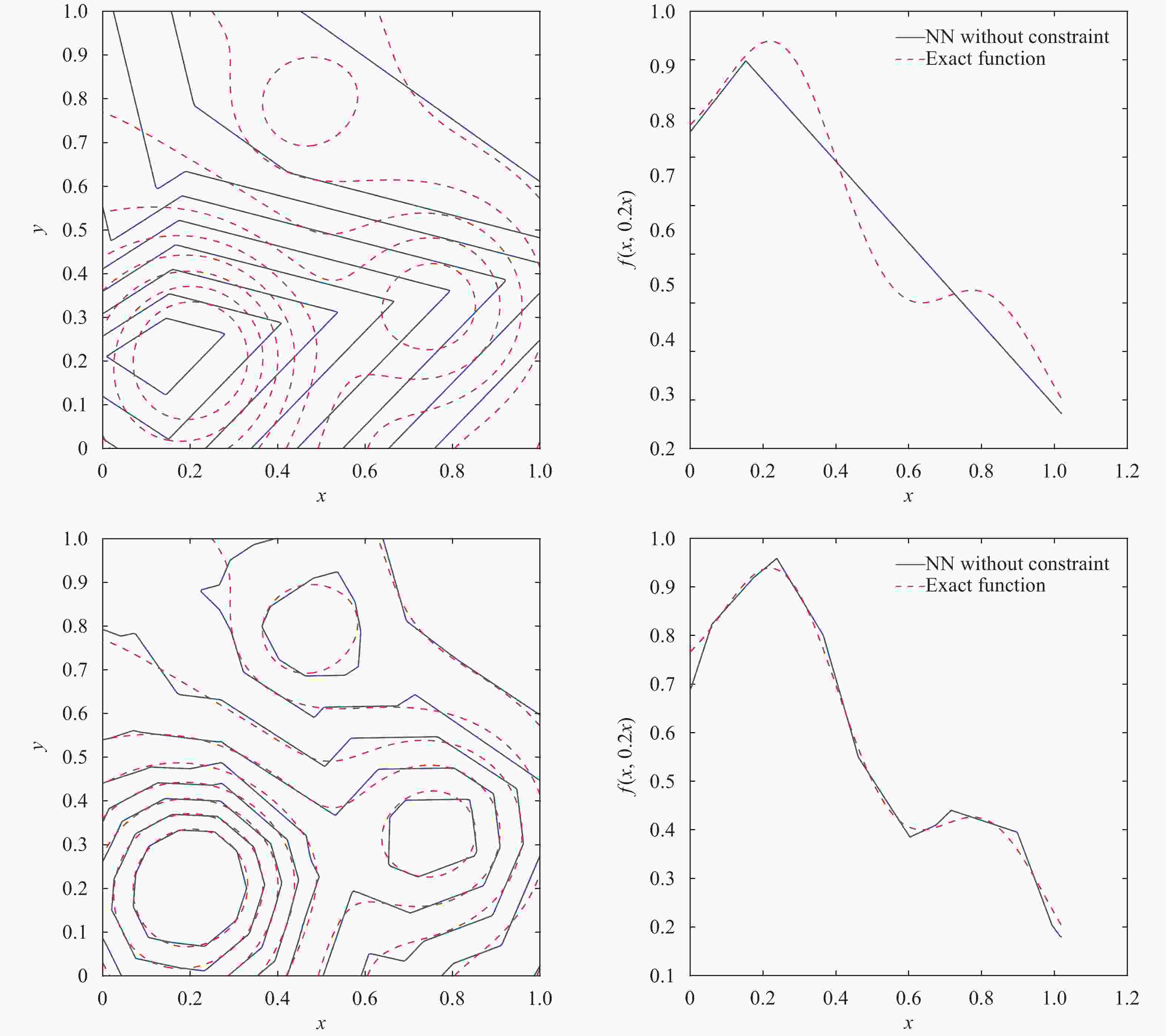
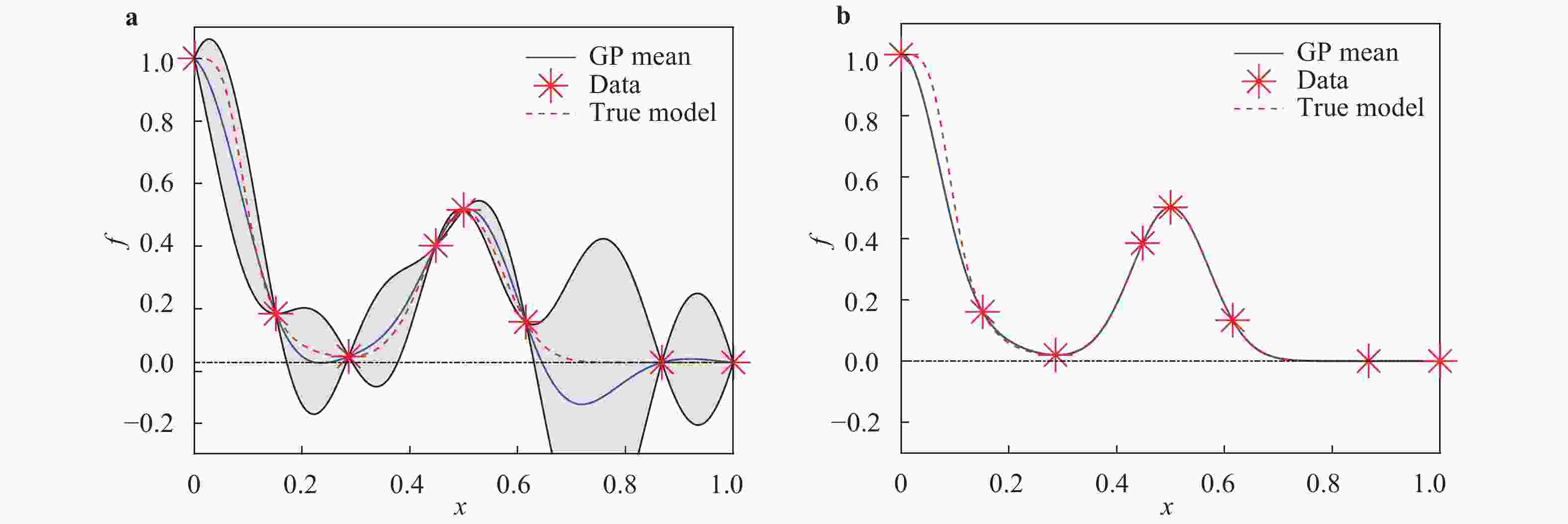
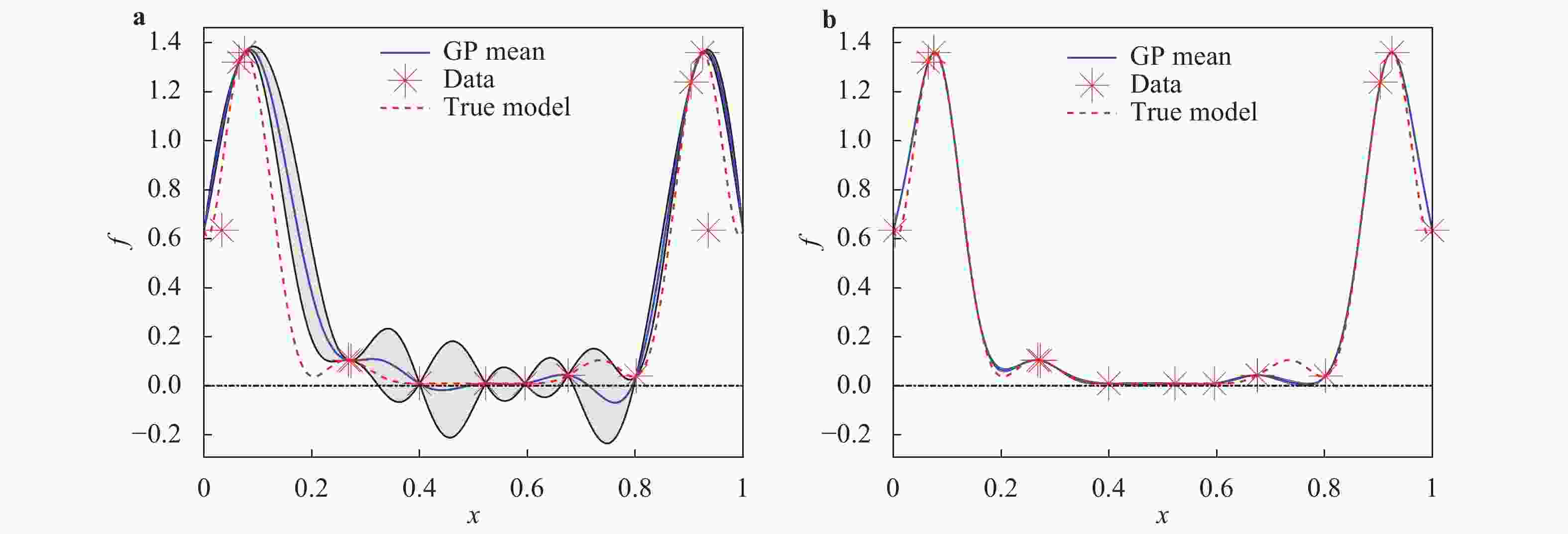
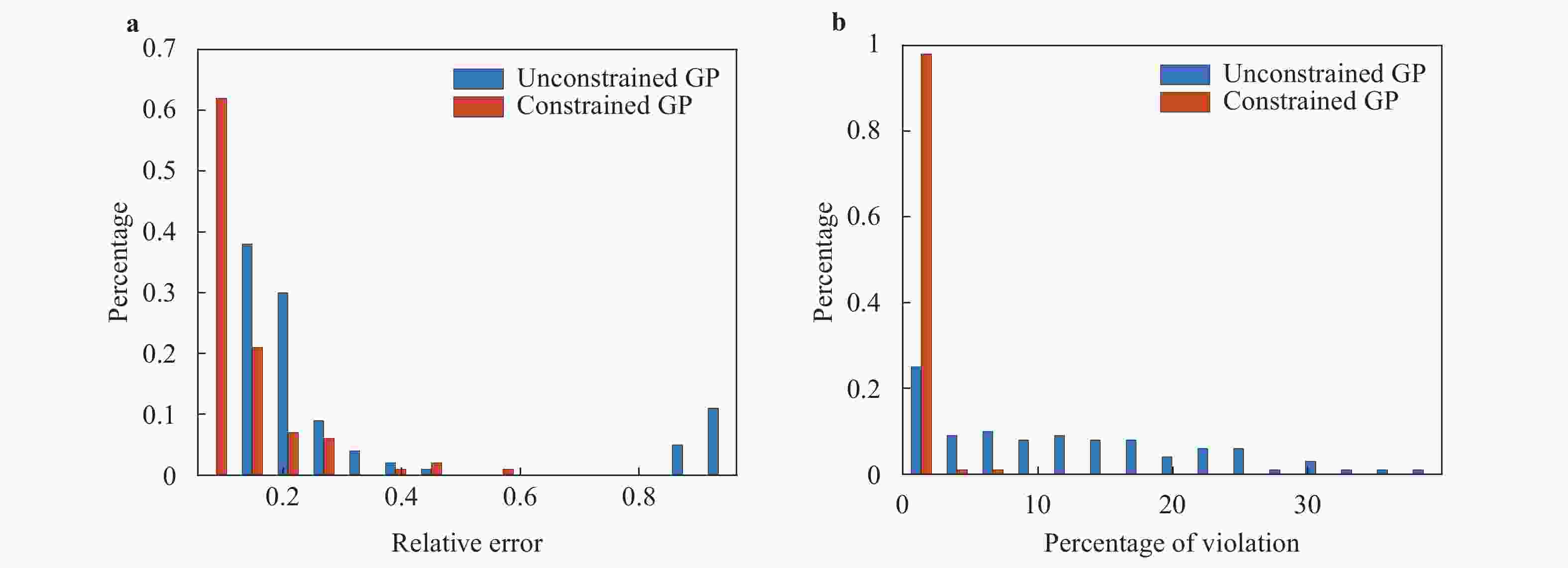
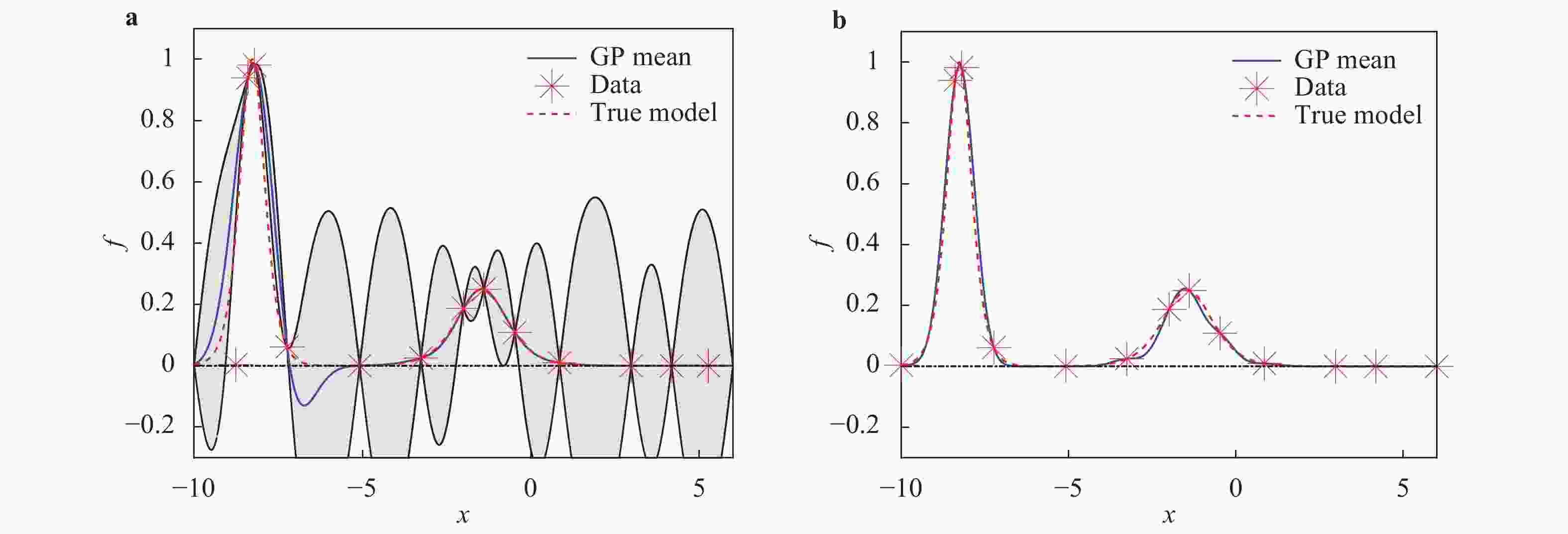
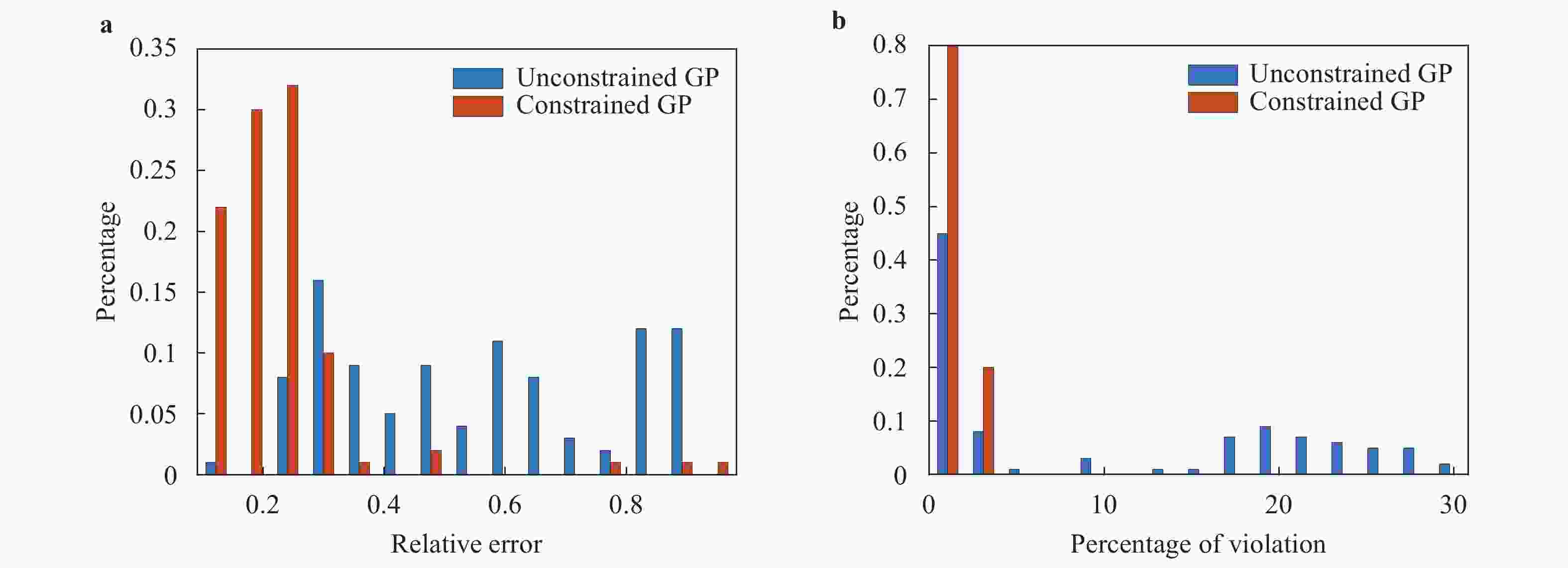
Theoretical and Applied Mechanics Letters 2020, 10(3): 182-187.
doi: 10.1016/j.taml.2020.01.036
Abstract:
Gaussian process (GP) regression is a flexible non-parametric approach to approximate complex models. In many cases, these models correspond to processes with bounded physical properties. Standard GP regression typically results in a proxy model which is unbounded for all temporal or spacial points, and thus leaves the possibility of taking on infeasible values. We propose an approach to enforce the physical constraints in a probabilistic way under the GP regression framework. In addition, this new approach reduces the variance in the resulting GP model.
Gaussian process (GP) regression is a flexible non-parametric approach to approximate complex models. In many cases, these models correspond to processes with bounded physical properties. Standard GP regression typically results in a proxy model which is unbounded for all temporal or spacial points, and thus leaves the possibility of taking on infeasible values. We propose an approach to enforce the physical constraints in a probabilistic way under the GP regression framework. In addition, this new approach reduces the variance in the resulting GP model.
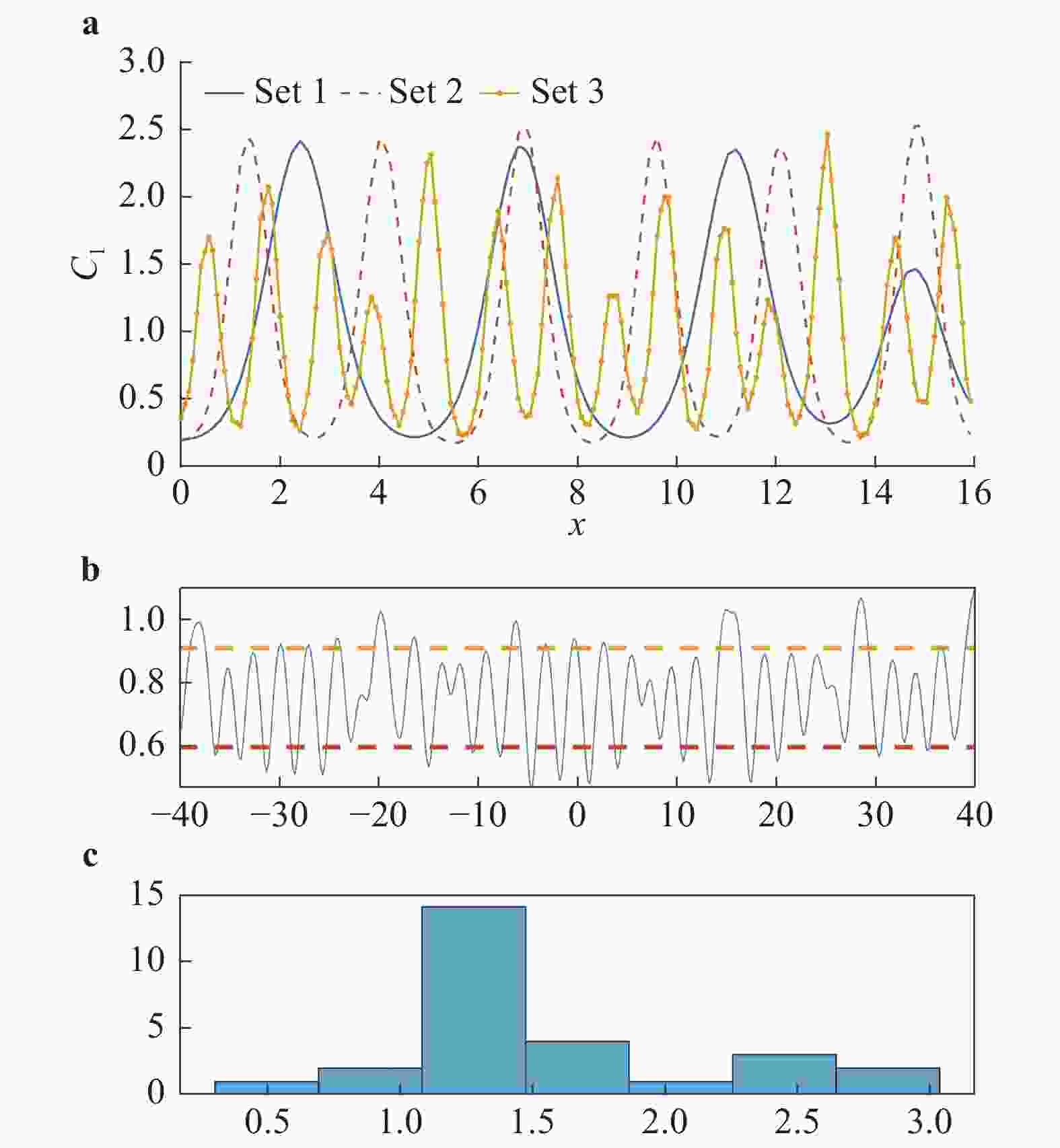
Theoretical and Applied Mechanics Letters 2020, 10(3): 188-194.
doi: 10.1016/j.taml.2020.01.028
Abstract:
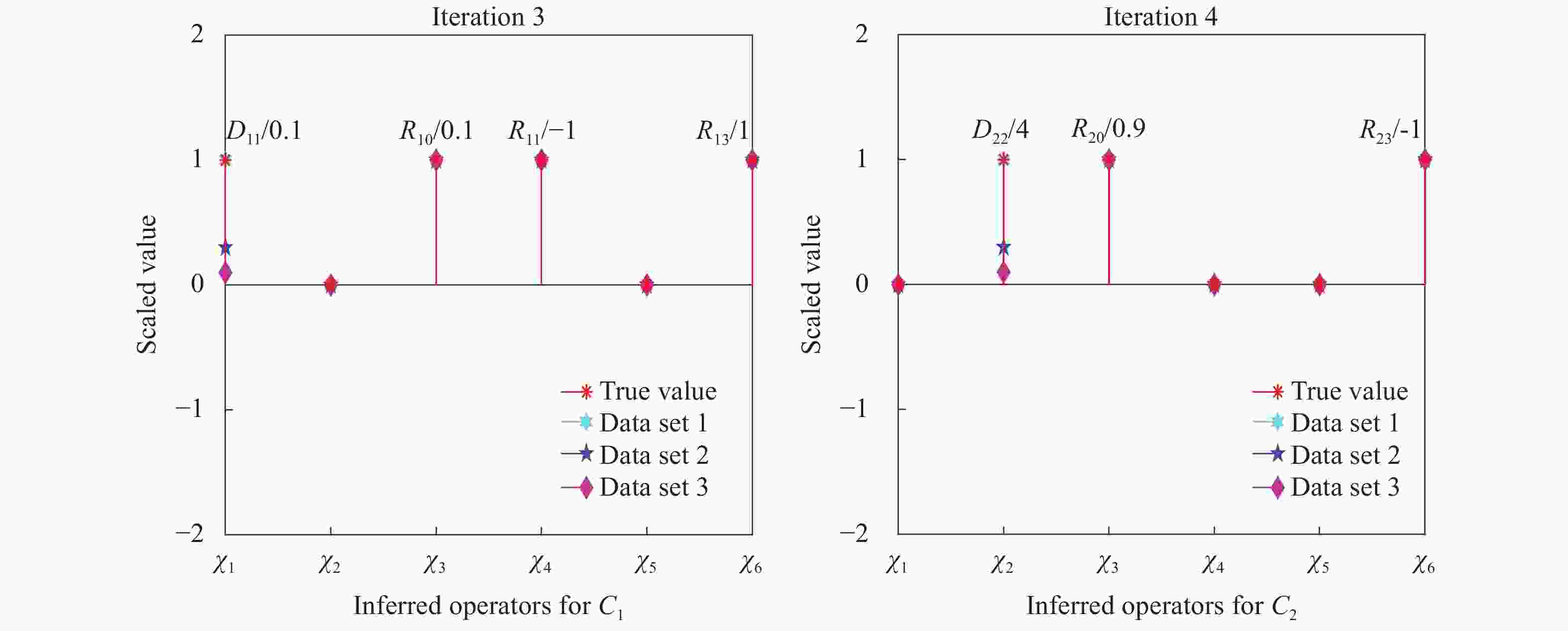
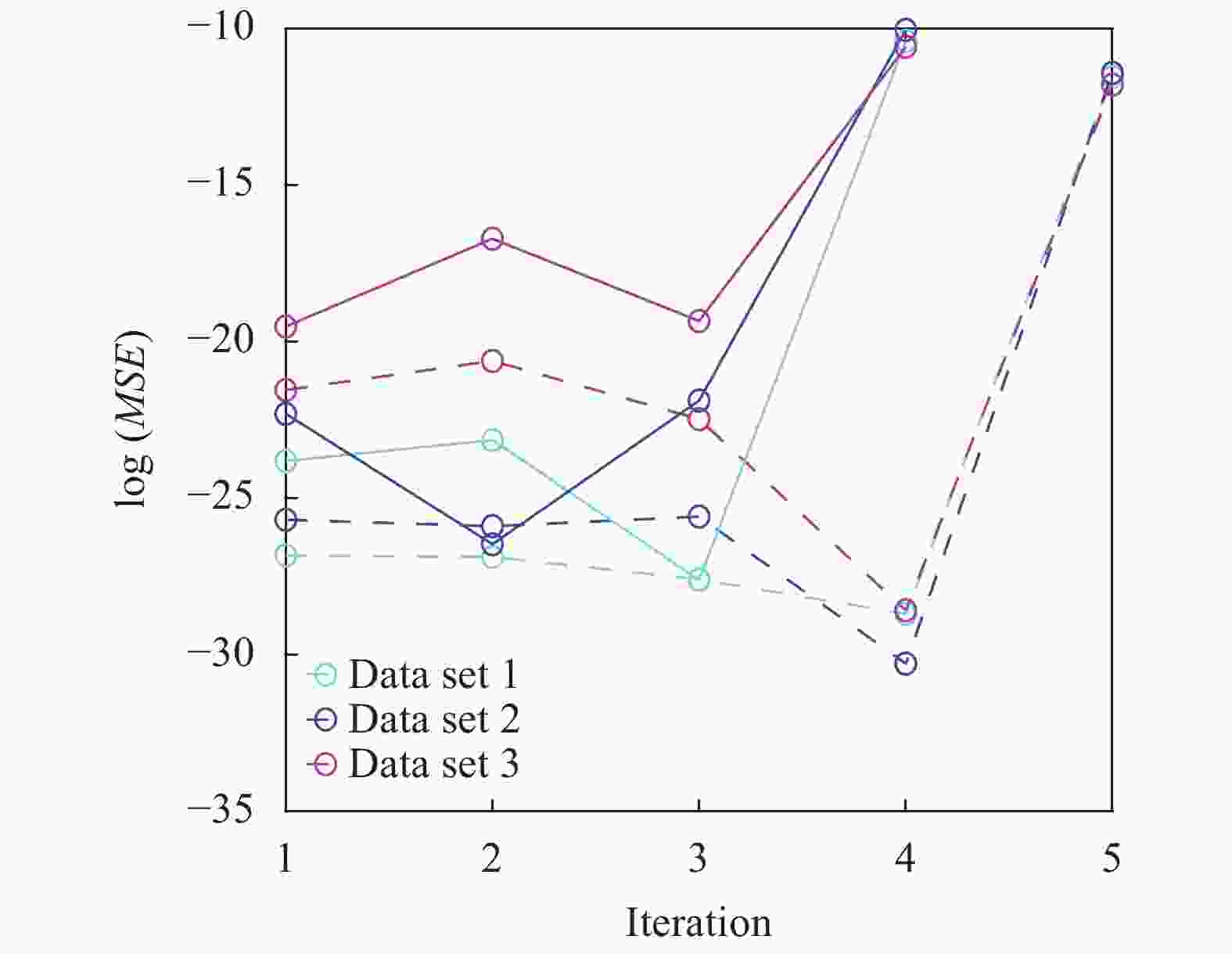
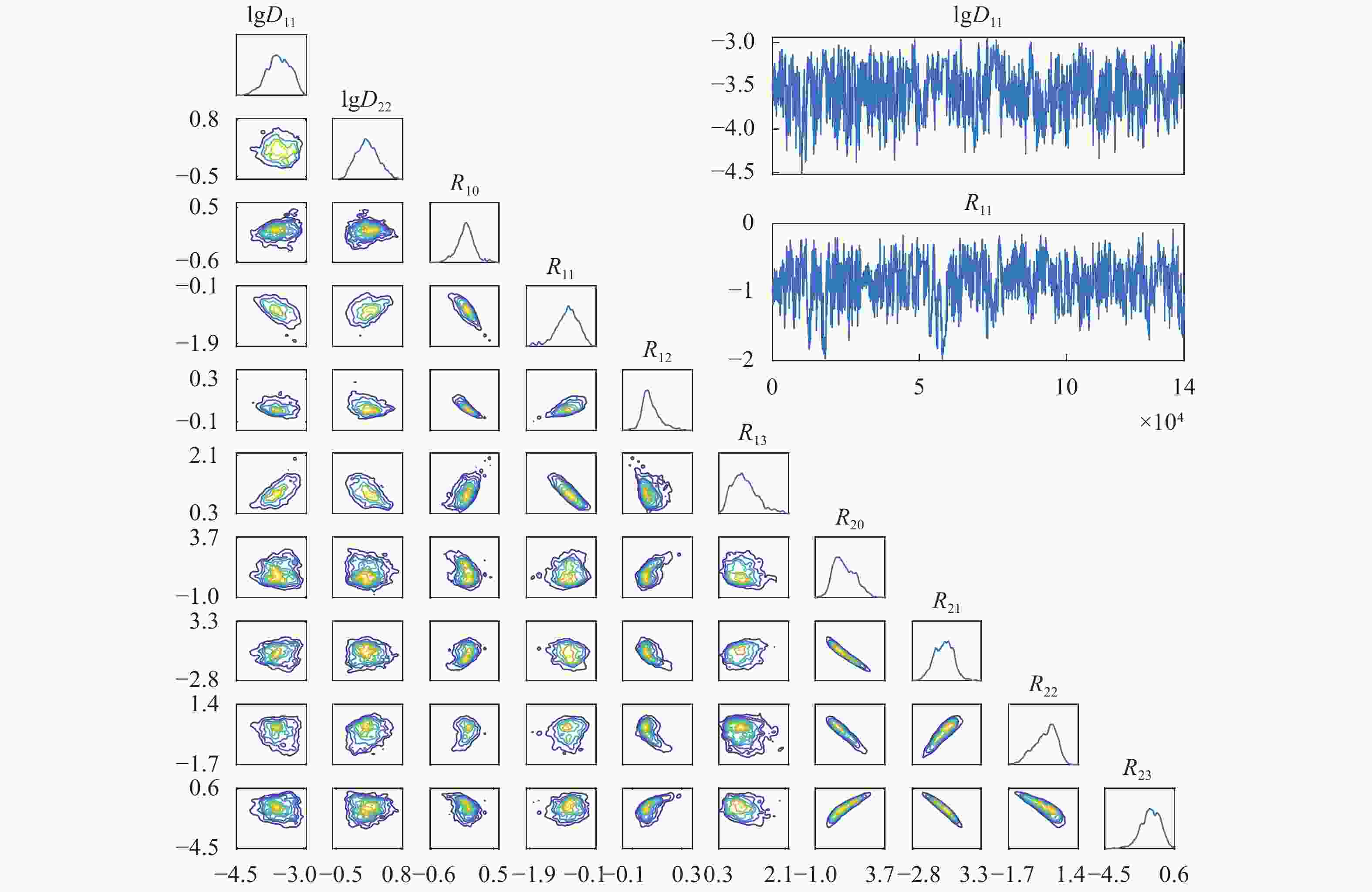
We present two approaches to system identification, i.e. the identification of partial differential equations (PDEs) from measurement data. The first is a regression-based variational system identification procedure that is advantageous in not requiring repeated forward model solves and has good scalability to large number of differential operators. However it has strict data type requirements needing the ability to directly represent the operators through the available data. The second is a Bayesian inference framework highly valuable for providing uncertainty quantification, and flexible for accommodating sparse and noisy data that may also be indirect quantities of interest. However, it also requires repeated forward solutions of the PDE models which is expensive and hinders scalability. We provide illustrations of results on a model problem for pattern formation dynamics, and discuss merits of the presented methods.
We present two approaches to system identification, i.e. the identification of partial differential equations (PDEs) from measurement data. The first is a regression-based variational system identification procedure that is advantageous in not requiring repeated forward model solves and has good scalability to large number of differential operators. However it has strict data type requirements needing the ability to directly represent the operators through the available data. The second is a Bayesian inference framework highly valuable for providing uncertainty quantification, and flexible for accommodating sparse and noisy data that may also be indirect quantities of interest. However, it also requires repeated forward solutions of the PDE models which is expensive and hinders scalability. We provide illustrations of results on a model problem for pattern formation dynamics, and discuss merits of the presented methods.
Theoretical and Applied Mechanics Letters 2020, 10(3): 195-201.
doi: 10.1016/j.taml.2020.01.027
Abstract:
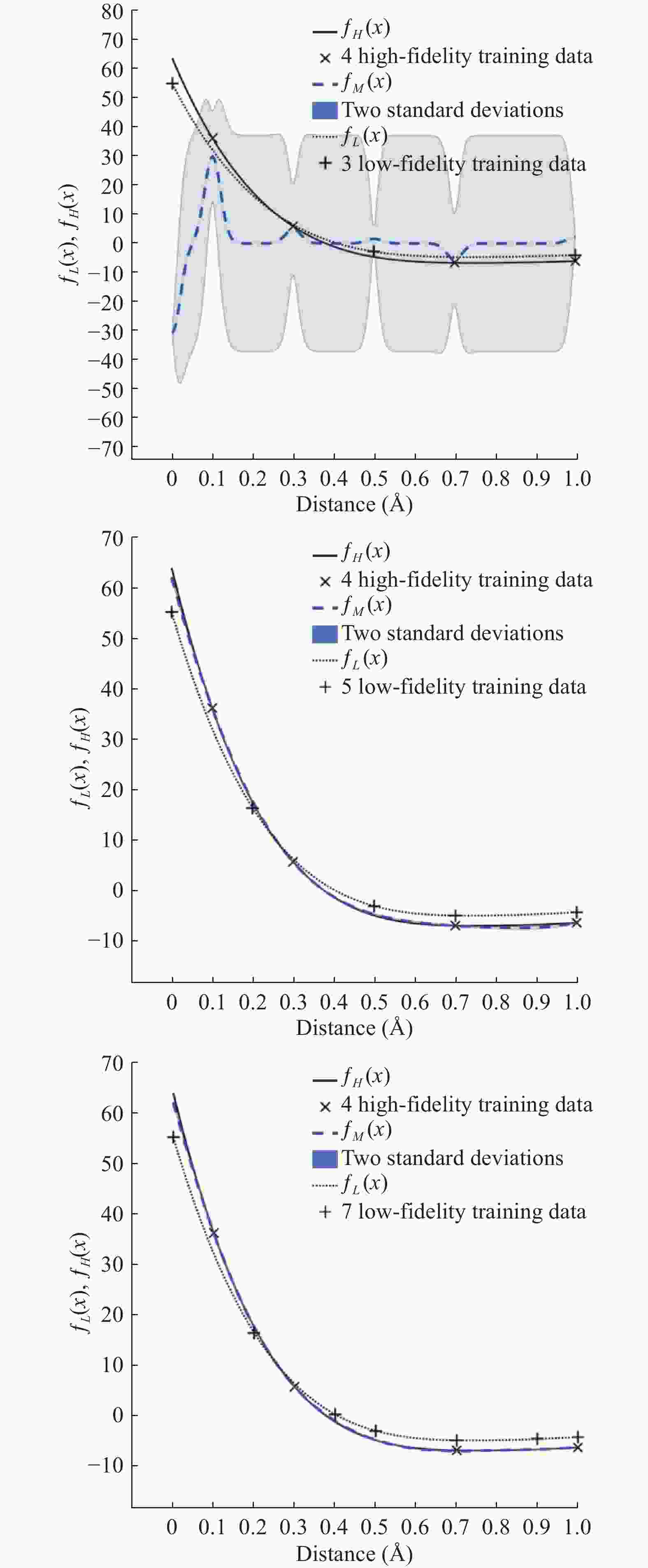
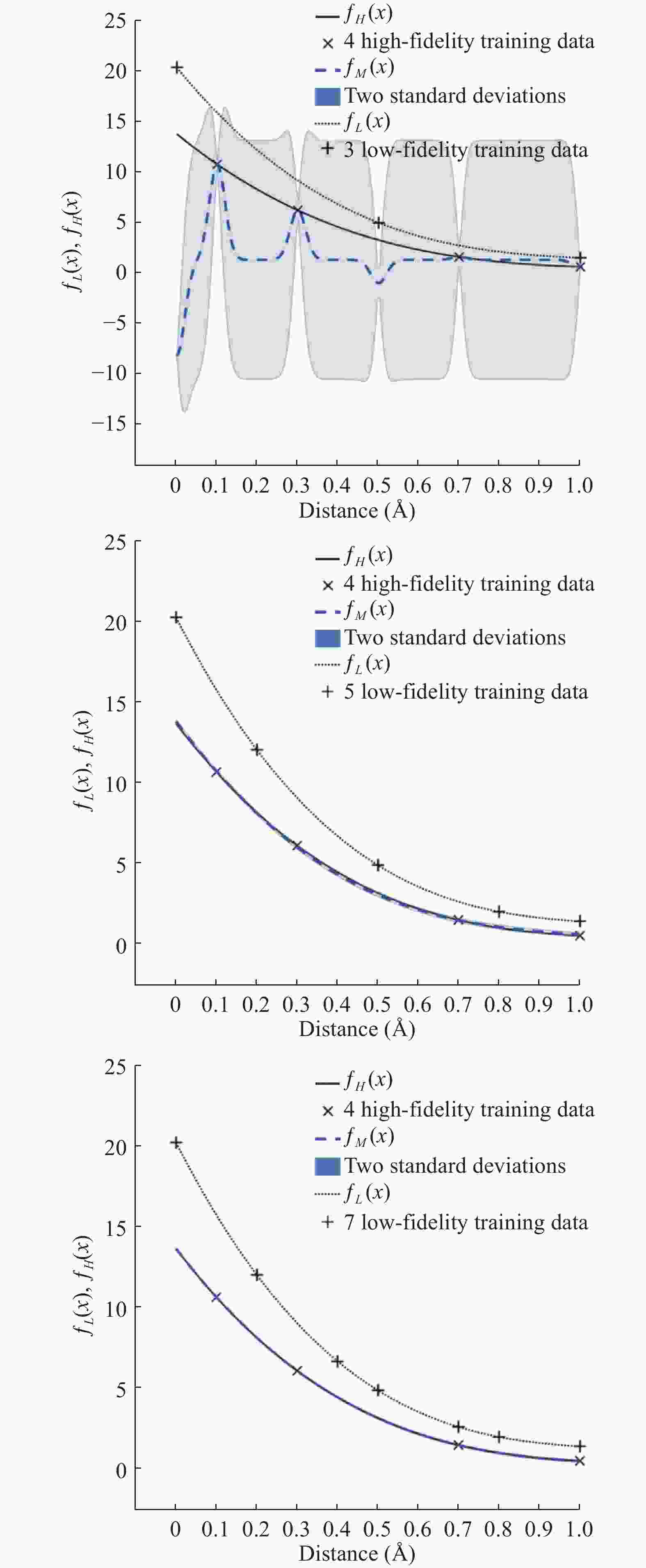
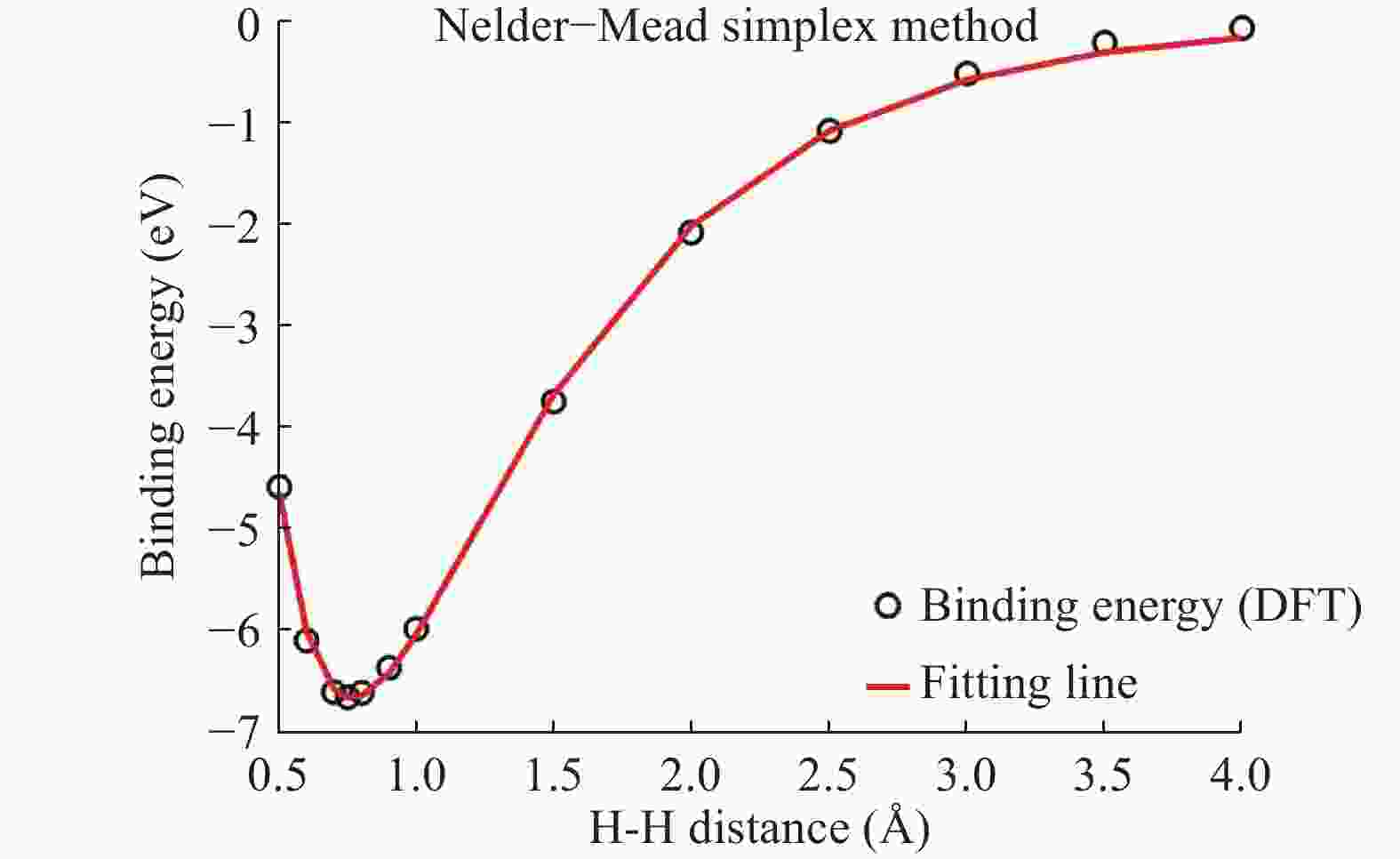
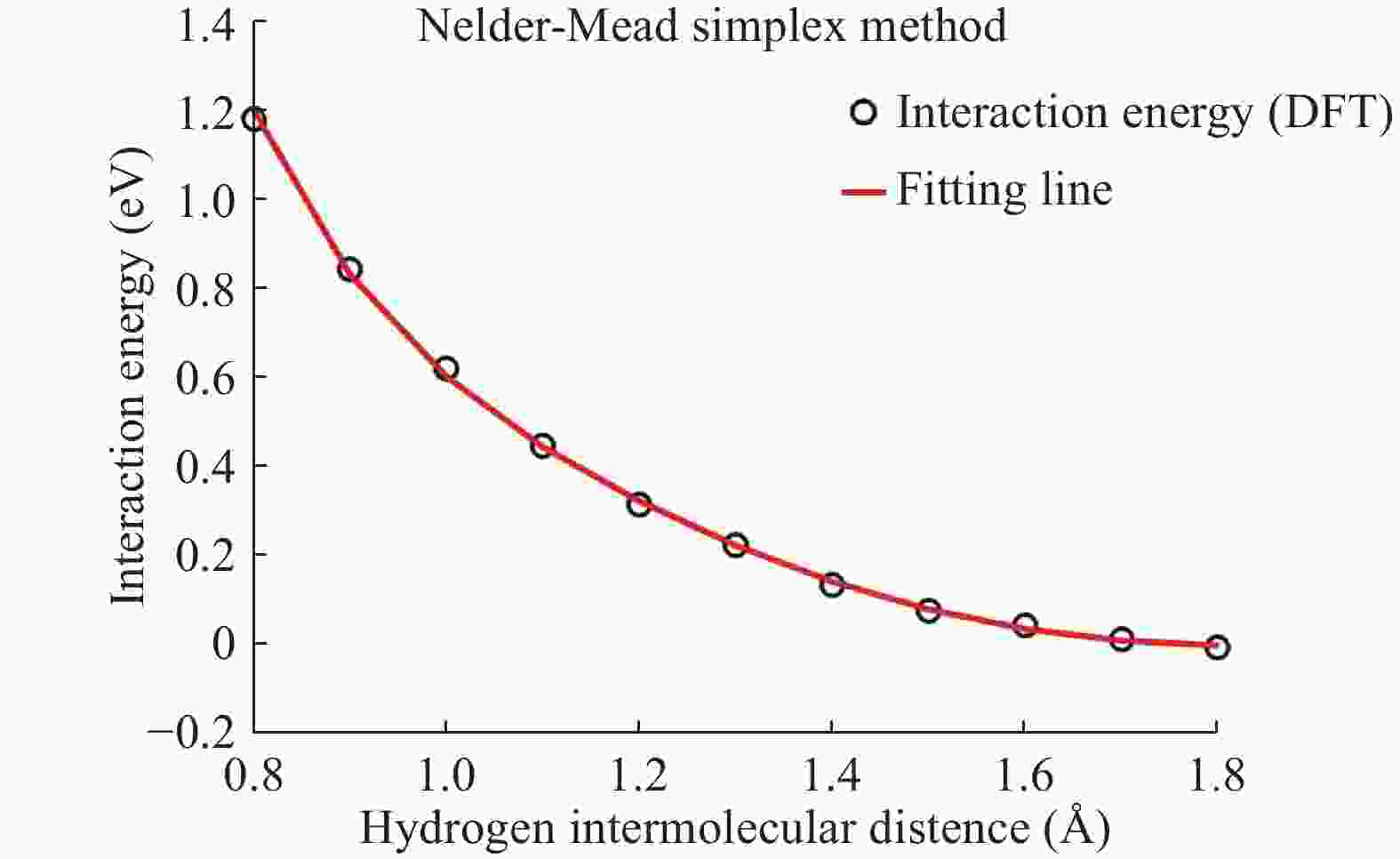
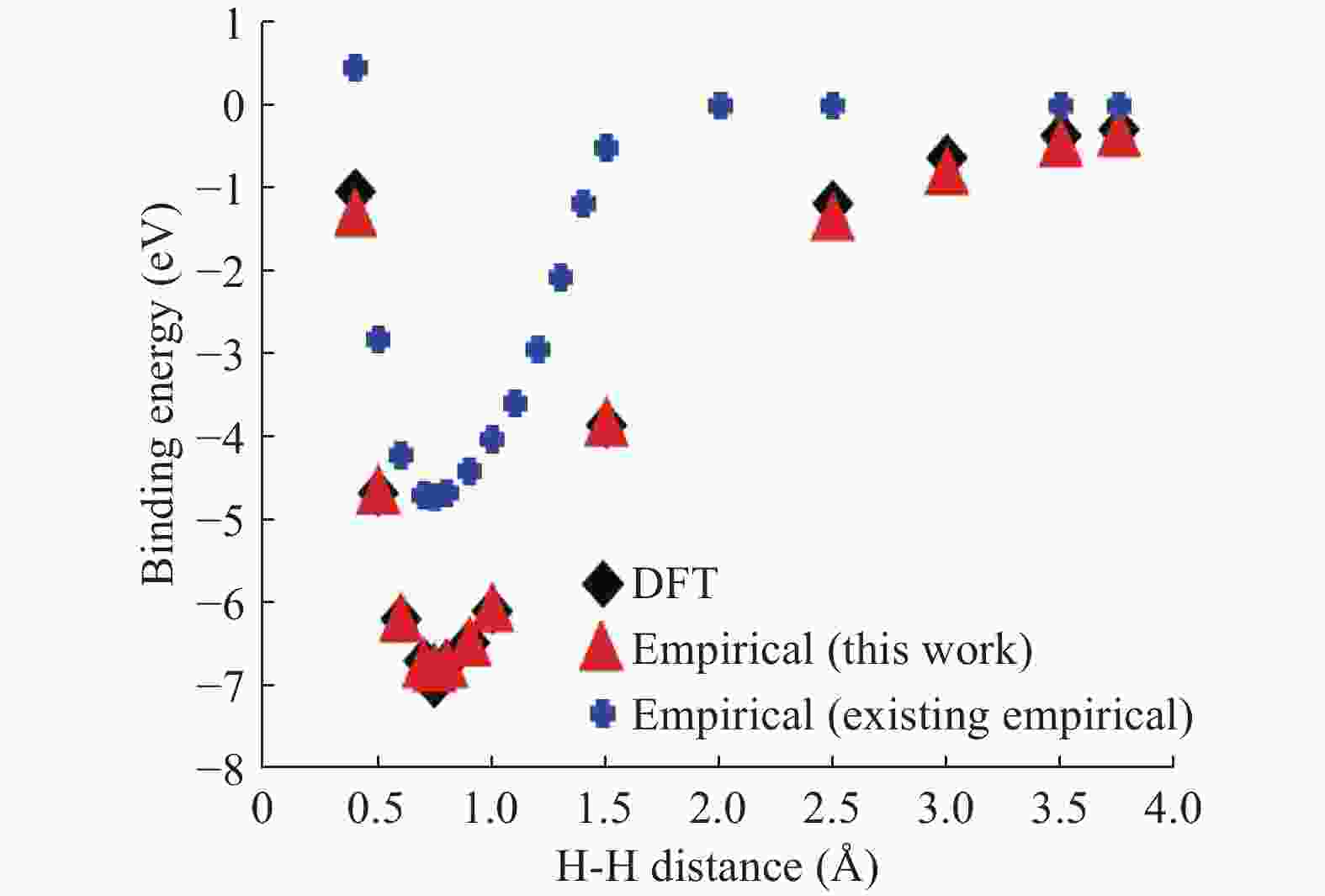
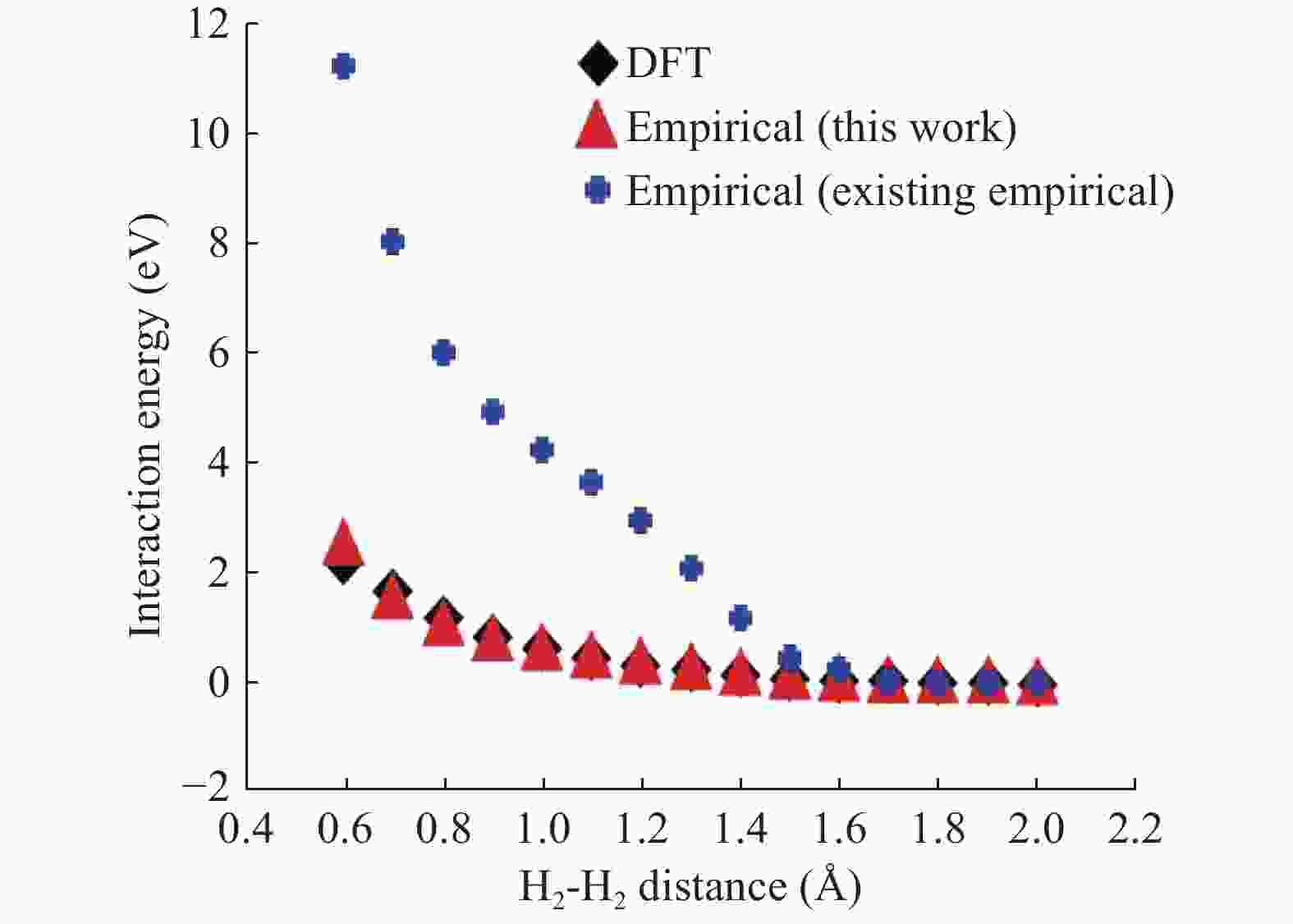
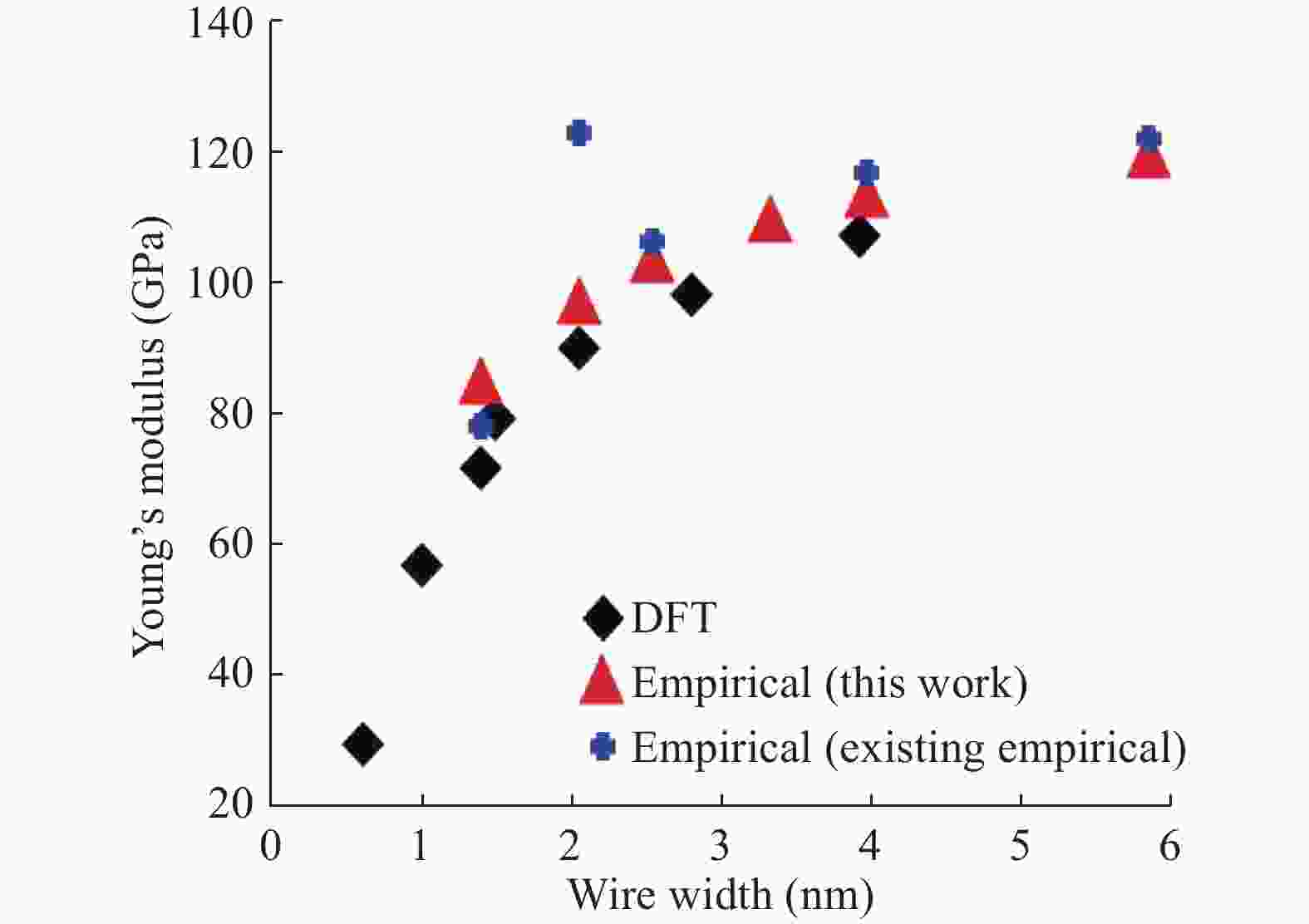
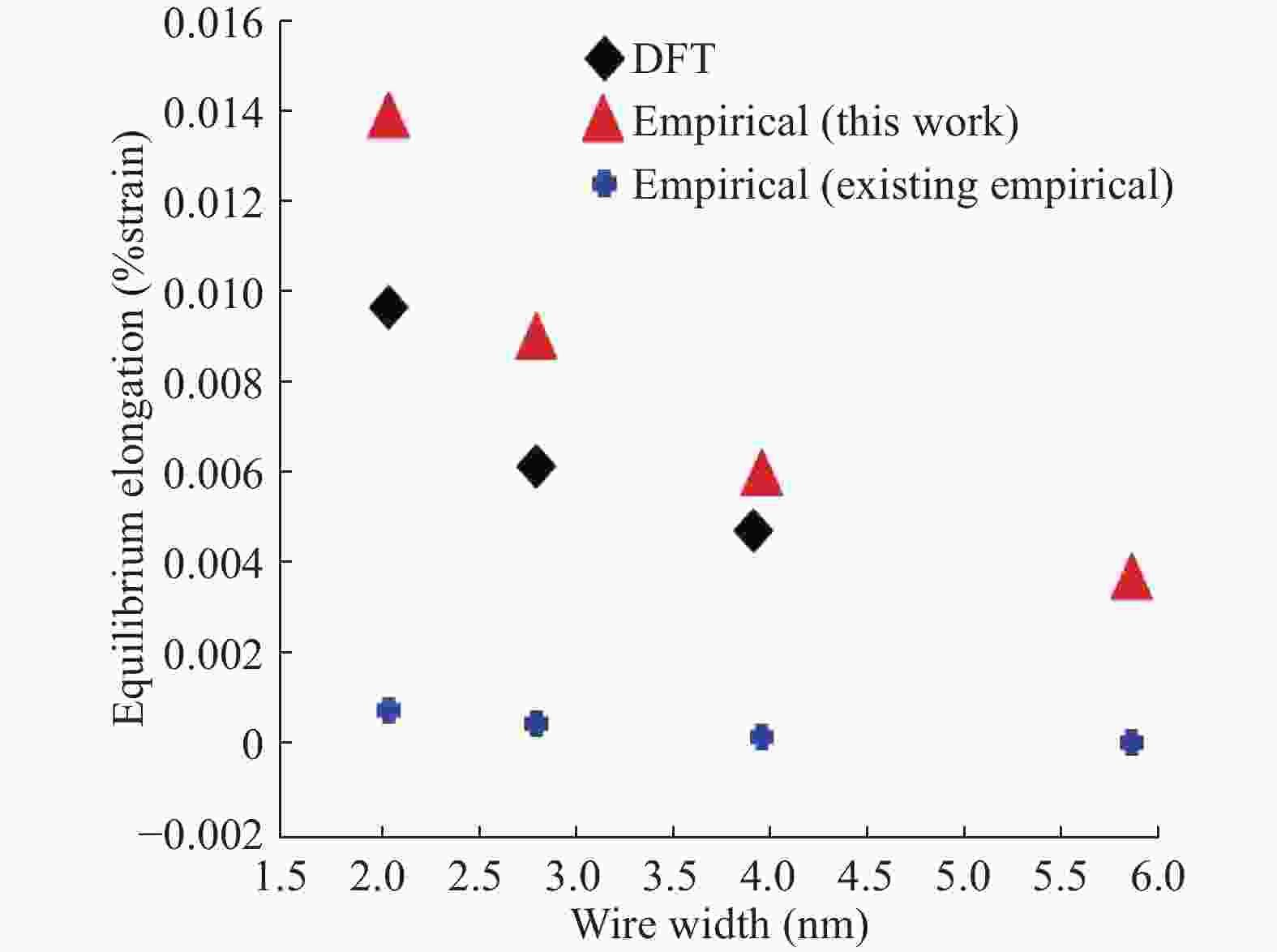
In material modeling, the calculation speed using the empirical potentials is fast compared to the first principle calculations, but the results are not as accurate as of the first principle calculations. First principle calculations are accurate but slow and very expensive to calculate. In this work, first, the H-H binding energy and H2-H2 interaction energy are calculated using the first principle calculations which can be applied to the Tersoff empirical potential. Second, the H-H parameters are estimated. After fitting H-H parameters, the mechanical properties are obtained. Finally, to integrate both the low-fidelity empirical potential data and the data from the high-fidelity first-principle calculations, the multi-fidelity Gaussian process regression is employed to predict the H-H binding energy and the H2-H2 interaction energy. Numerical results demonstrate the accuracy of the developed empirical potentials.
In material modeling, the calculation speed using the empirical potentials is fast compared to the first principle calculations, but the results are not as accurate as of the first principle calculations. First principle calculations are accurate but slow and very expensive to calculate. In this work, first, the H-H binding energy and H2-H2 interaction energy are calculated using the first principle calculations which can be applied to the Tersoff empirical potential. Second, the H-H parameters are estimated. After fitting H-H parameters, the mechanical properties are obtained. Finally, to integrate both the low-fidelity empirical potential data and the data from the high-fidelity first-principle calculations, the multi-fidelity Gaussian process regression is employed to predict the H-H binding energy and the H2-H2 interaction energy. Numerical results demonstrate the accuracy of the developed empirical potentials.
Theoretical and Applied Mechanics Letters 2020, 10(3): 202-206.
doi: 10.1016/j.taml.2020.01.038
Abstract:
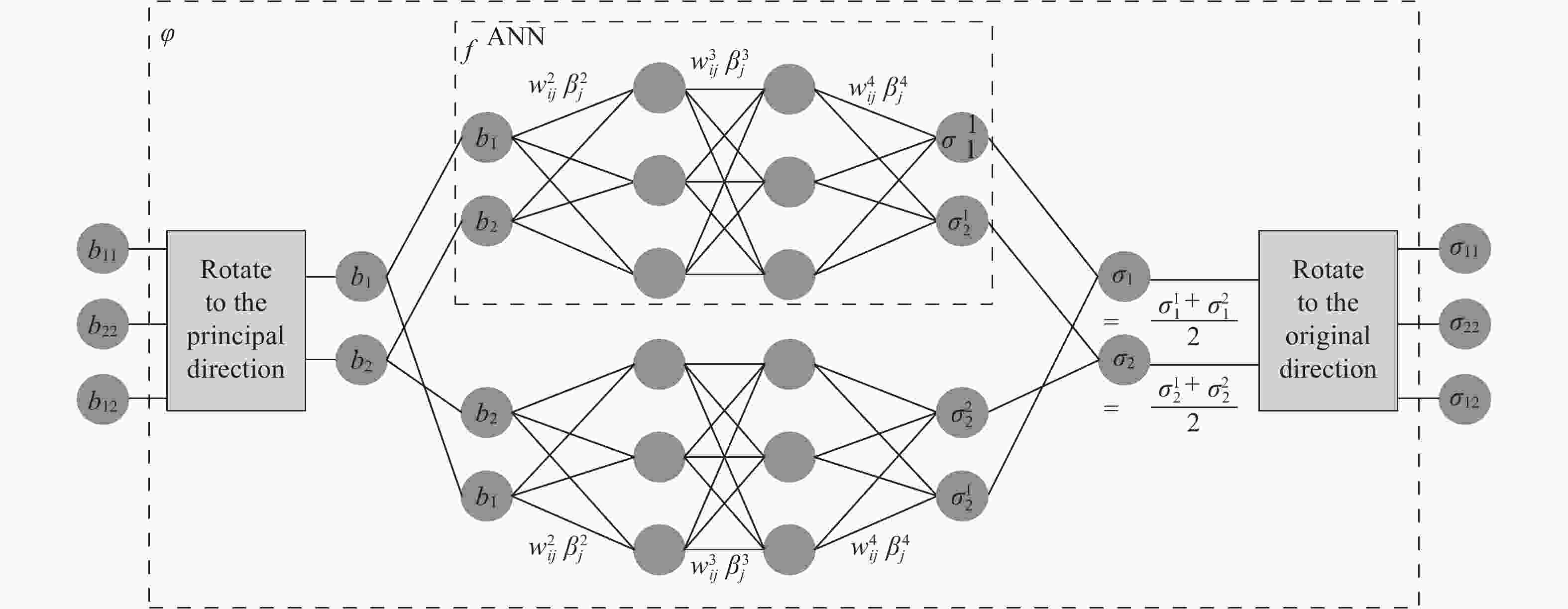
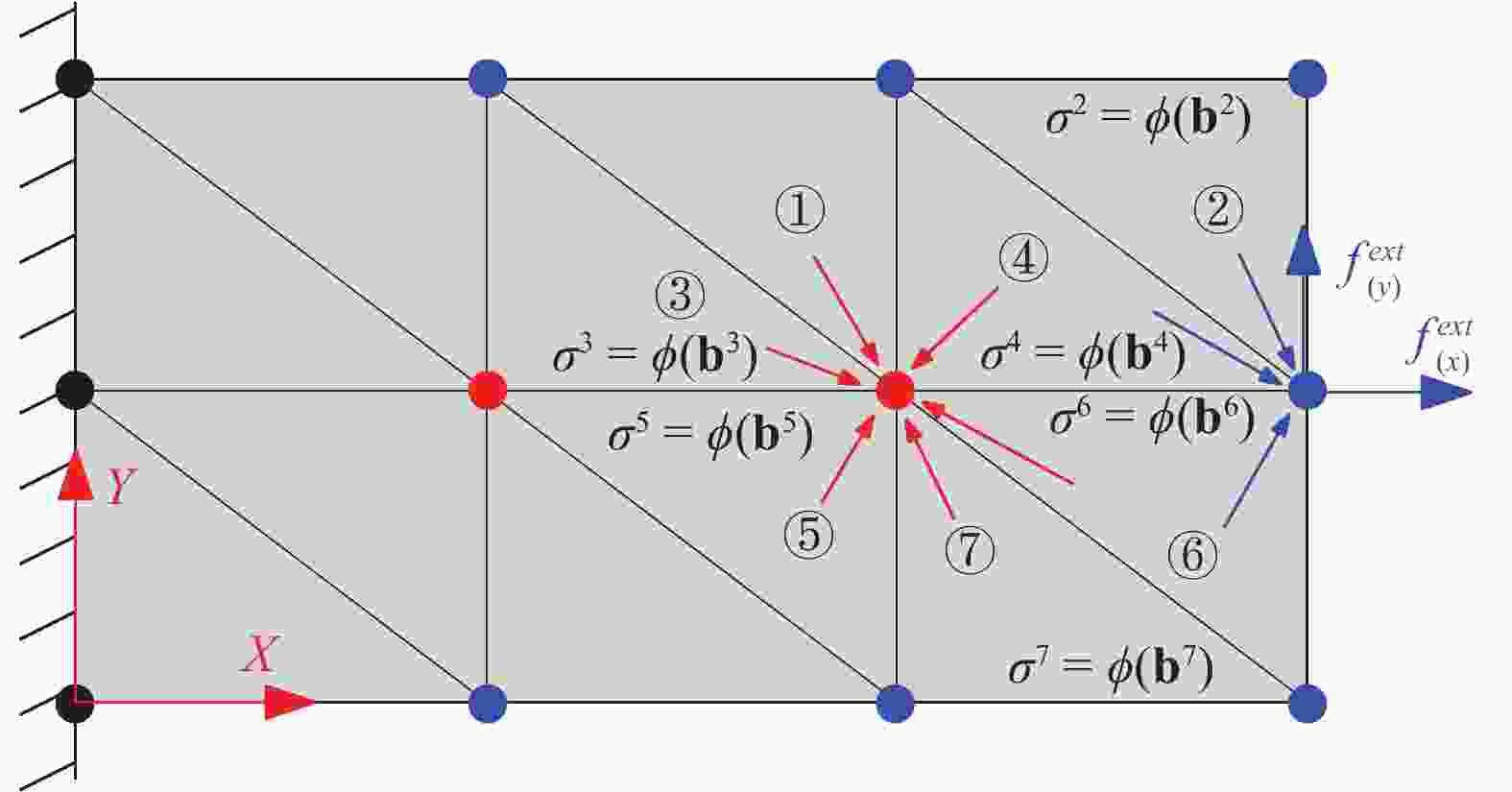
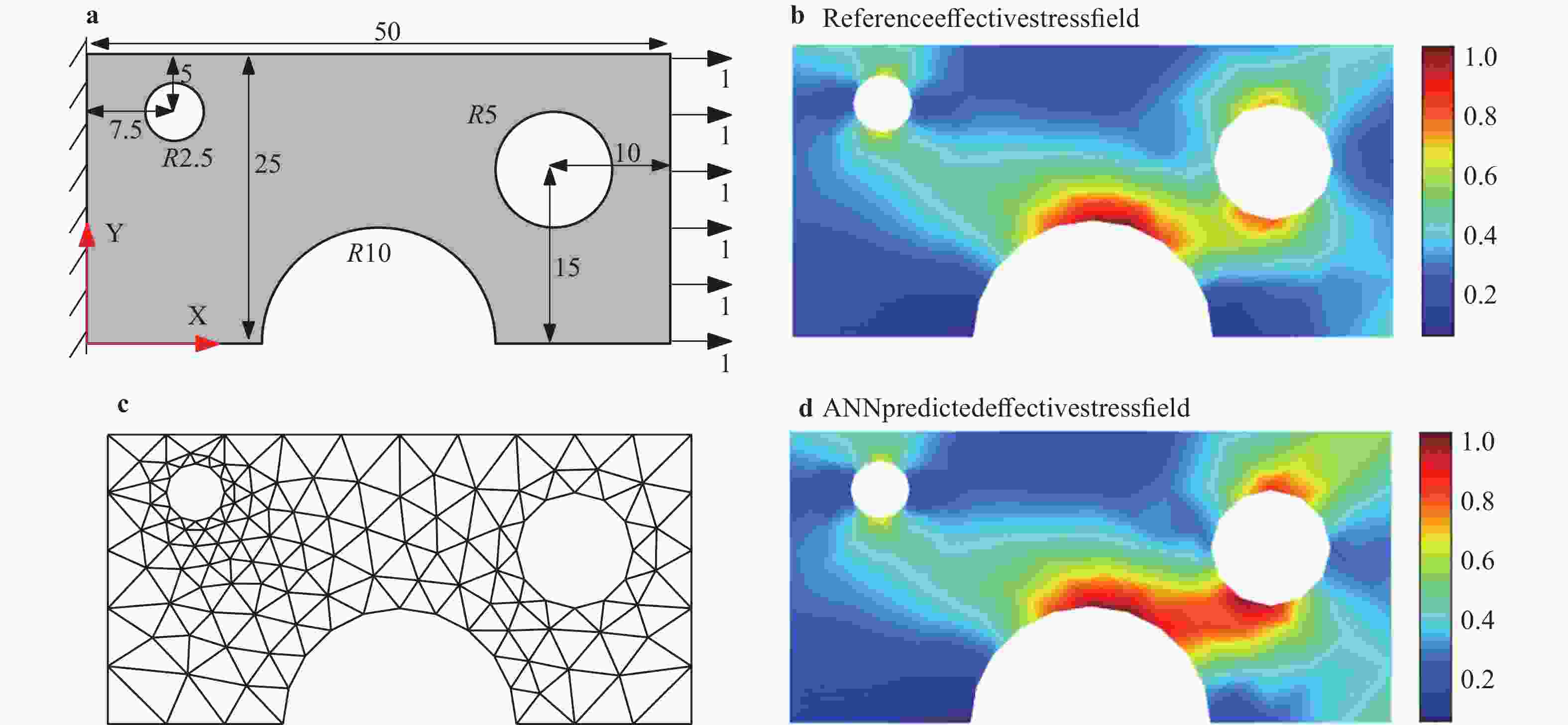
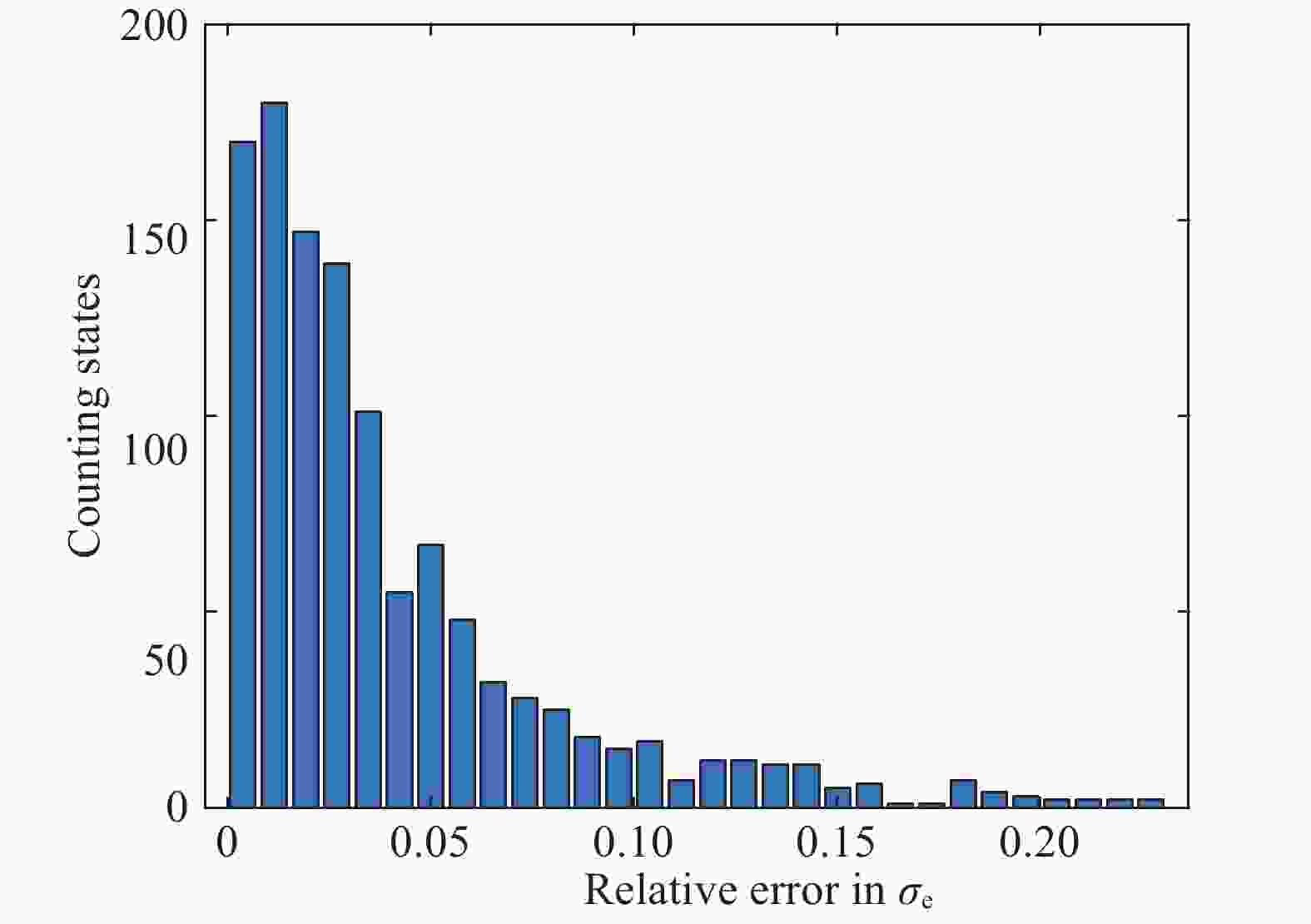
The recently developed data-driven approach can establish the material law for nonlinear elastic composite materials (especially newly developed materials) by the generated stress-strain data under different loading paths (Computational Mechanics, 2019). Generally, the displacement (or strain) fields can be obtained relatively easier using digital image correlation (DIC) technique experimentally, but the stress field is hard to be measured. This situation limits the applicability of the proposed data-driven approach. In this paper, a method based on artificial neural network (ANN) to identify stress fields and further obtain the material law of nonlinear elastic materials is presented, which can make the proposed data-driven approach more practical. A numerical example is given to prove the validity of the method. The limitations of the proposed approach are also discussed.
The recently developed data-driven approach can establish the material law for nonlinear elastic composite materials (especially newly developed materials) by the generated stress-strain data under different loading paths (Computational Mechanics, 2019). Generally, the displacement (or strain) fields can be obtained relatively easier using digital image correlation (DIC) technique experimentally, but the stress field is hard to be measured. This situation limits the applicability of the proposed data-driven approach. In this paper, a method based on artificial neural network (ANN) to identify stress fields and further obtain the material law of nonlinear elastic materials is presented, which can make the proposed data-driven approach more practical. A numerical example is given to prove the validity of the method. The limitations of the proposed approach are also discussed.
Theoretical and Applied Mechanics Letters 2020, 10(3): 207-212.
doi: 10.1016/j.taml.2020.01.039
Abstract:
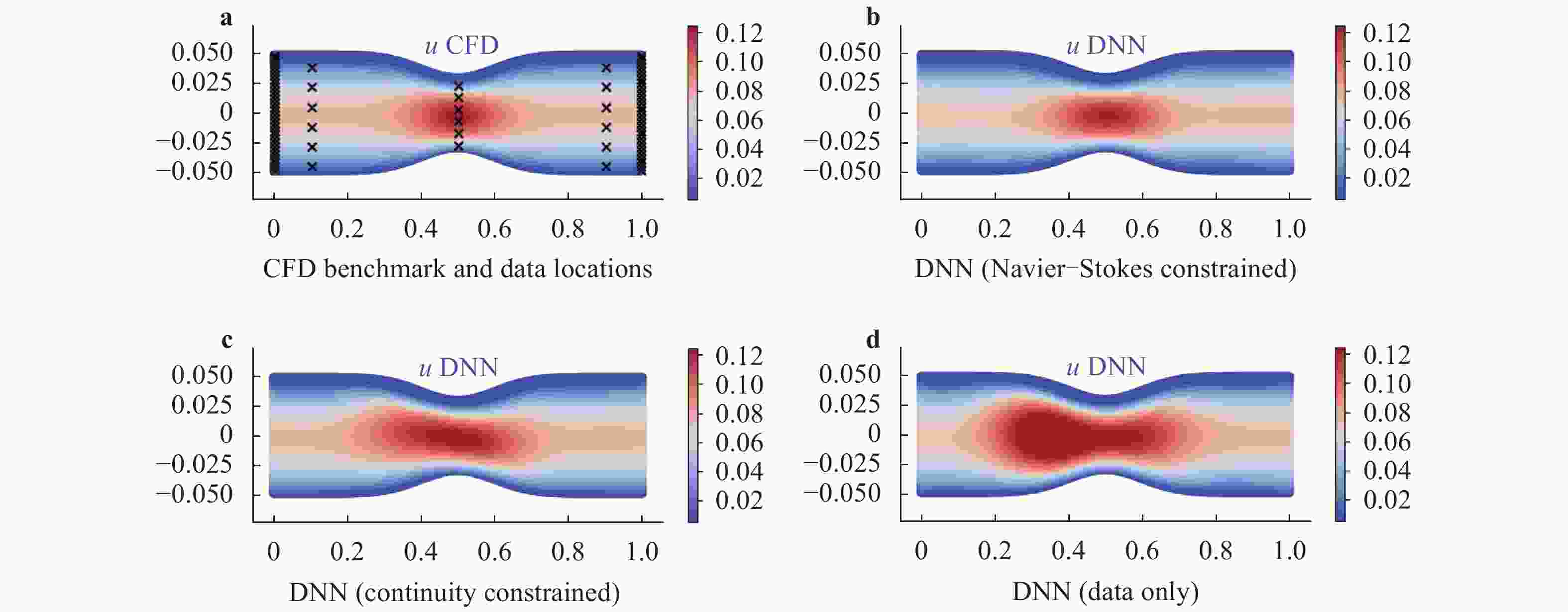
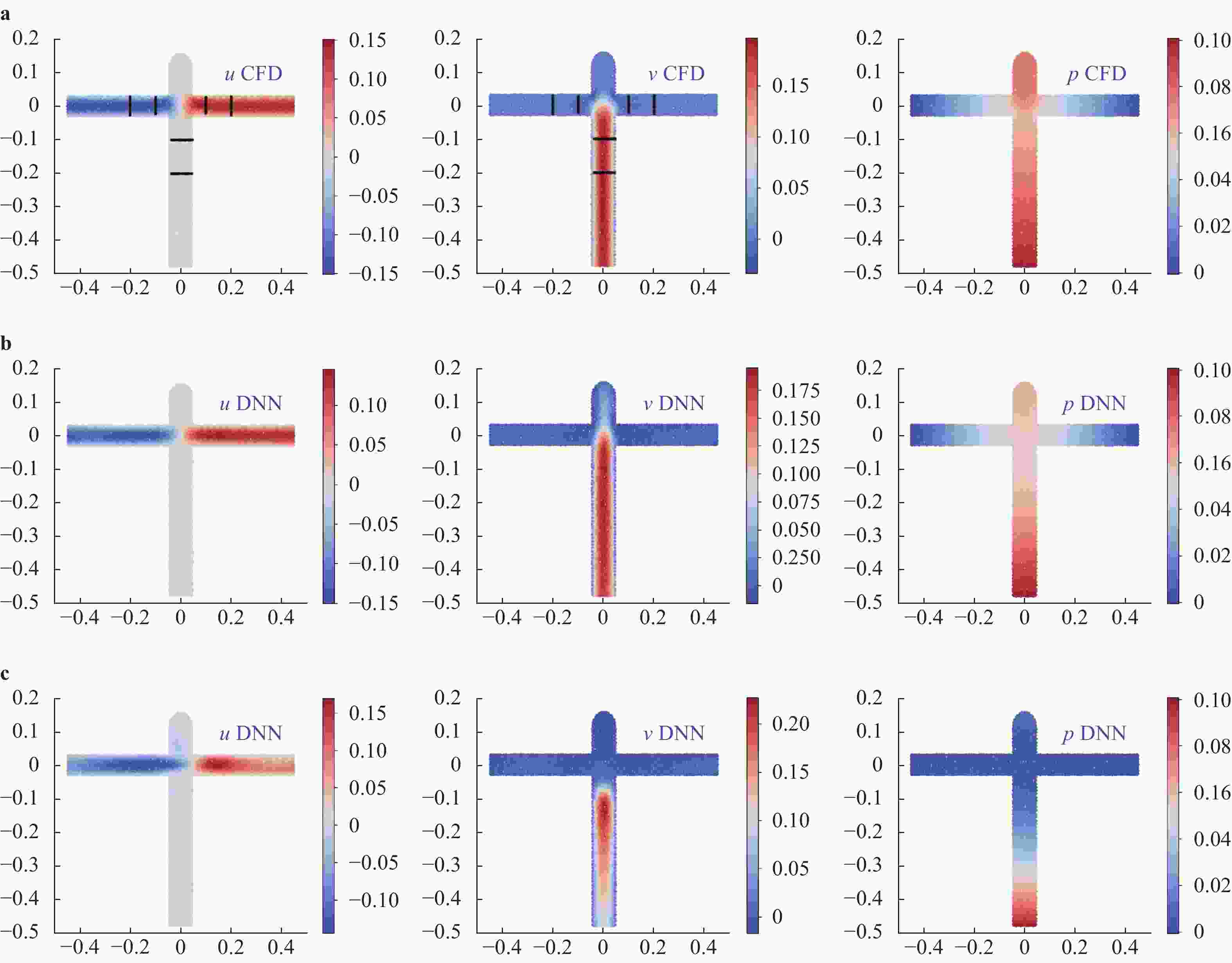
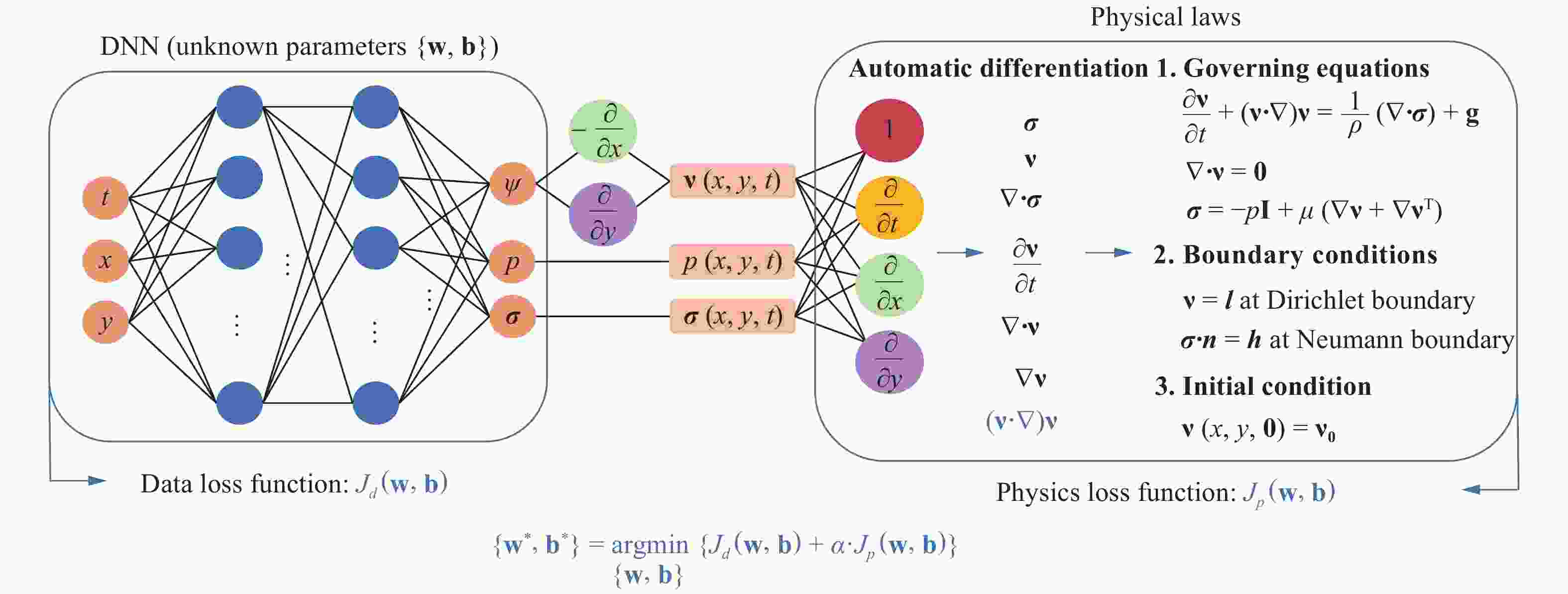
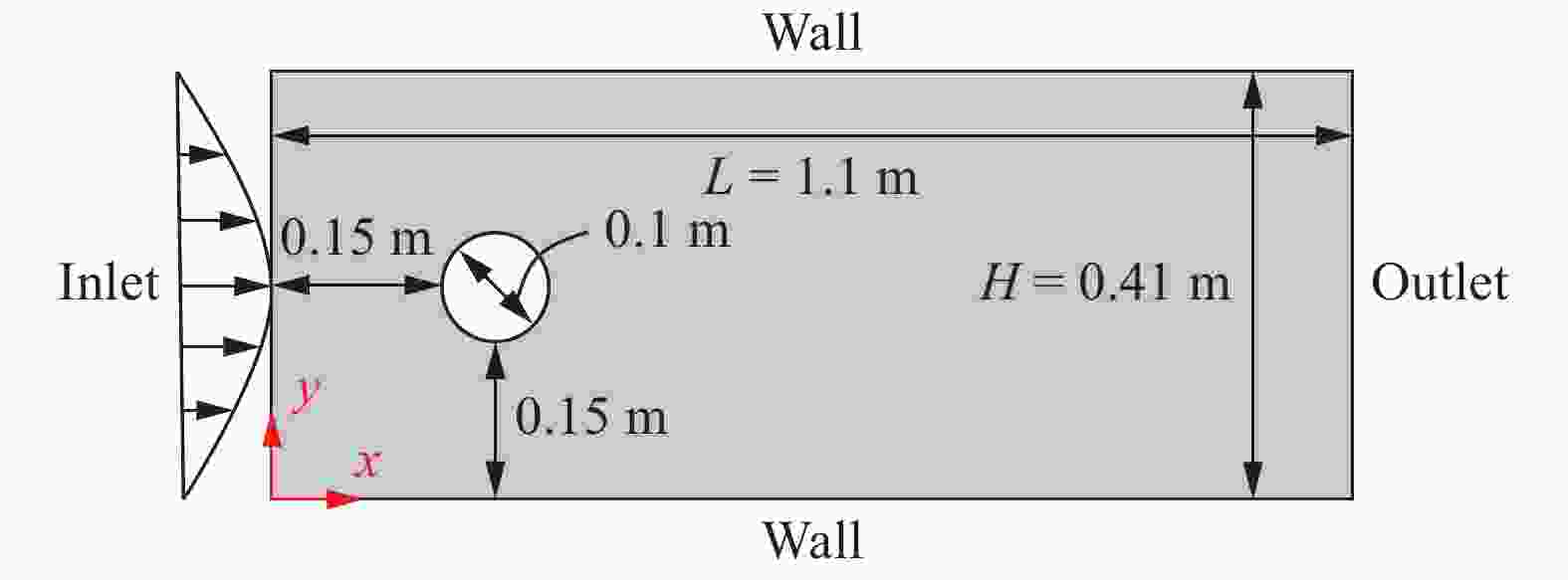
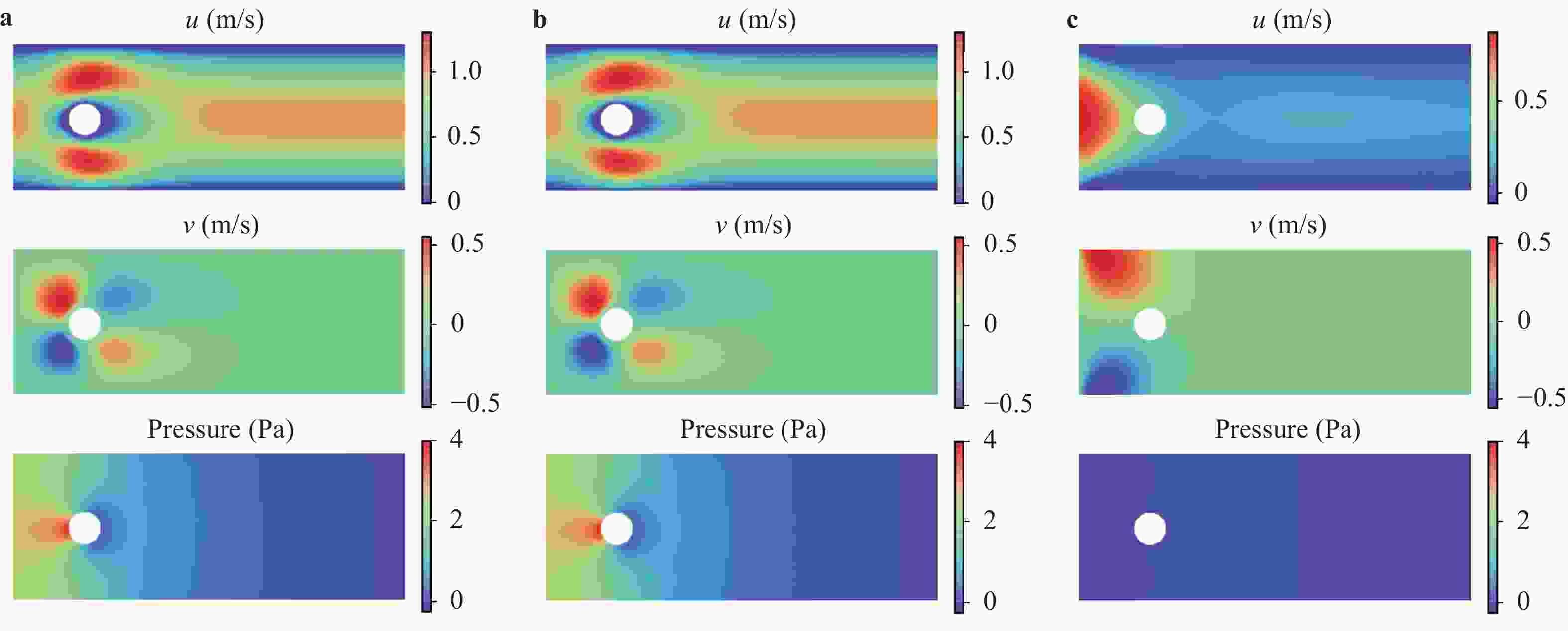
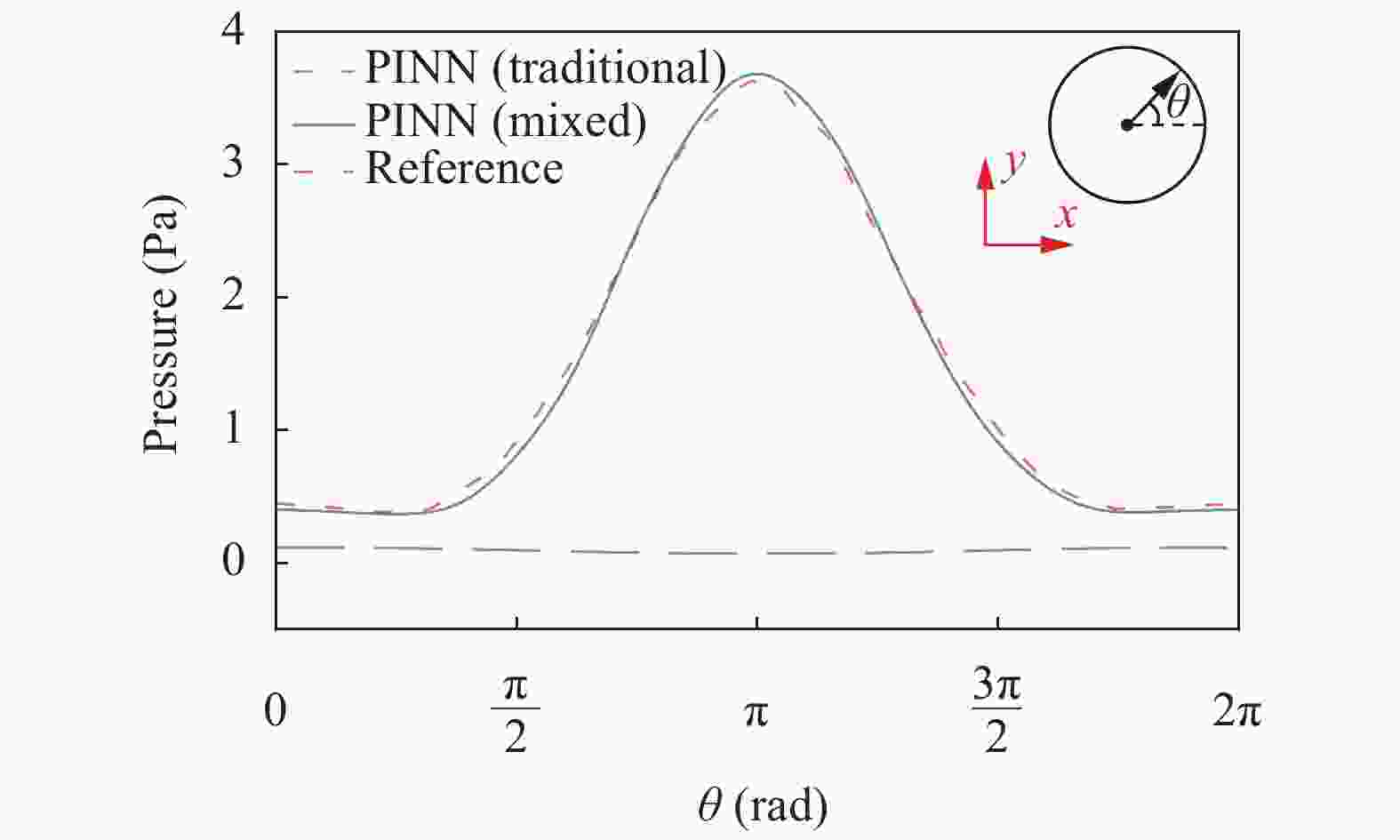
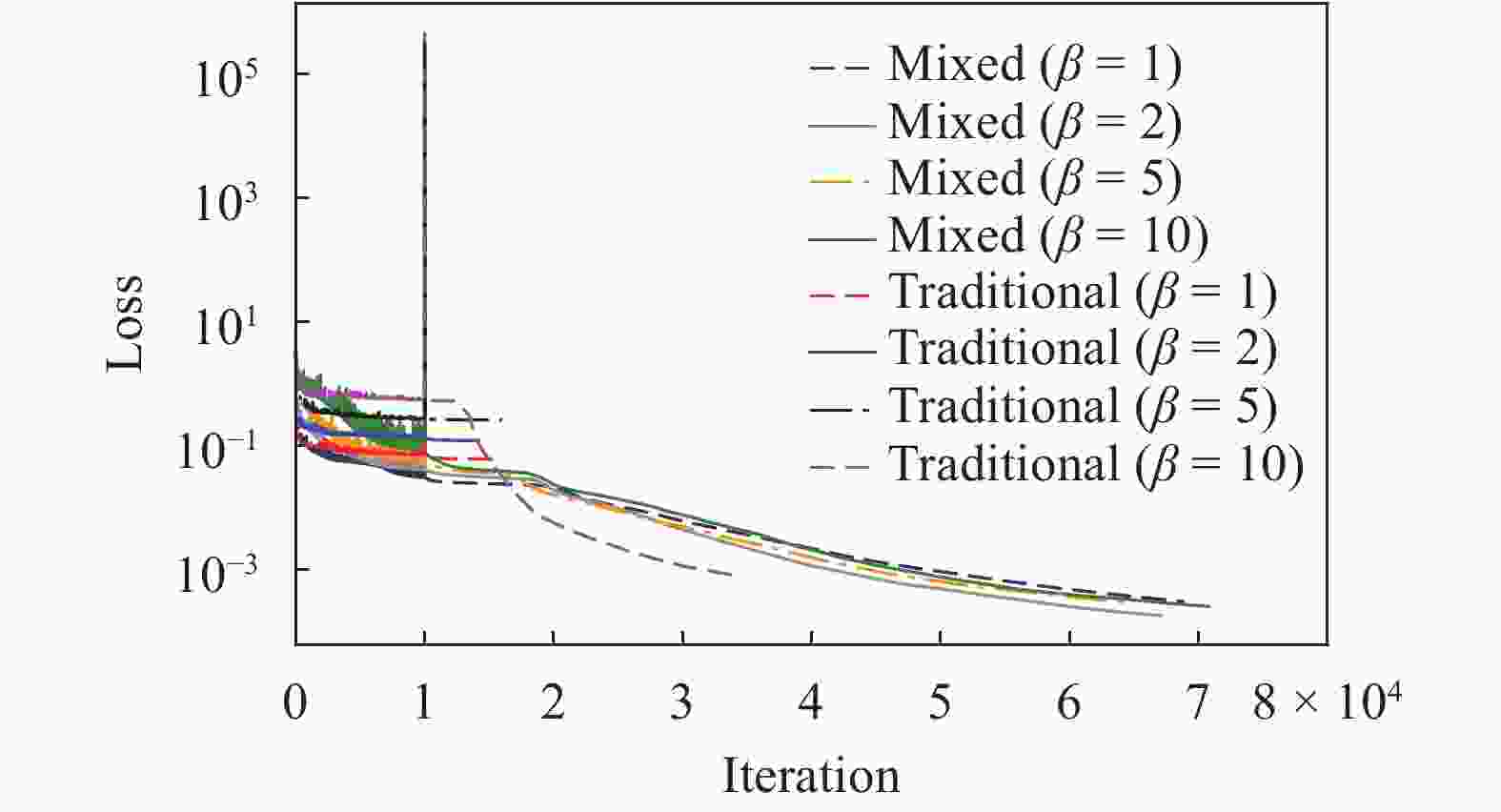
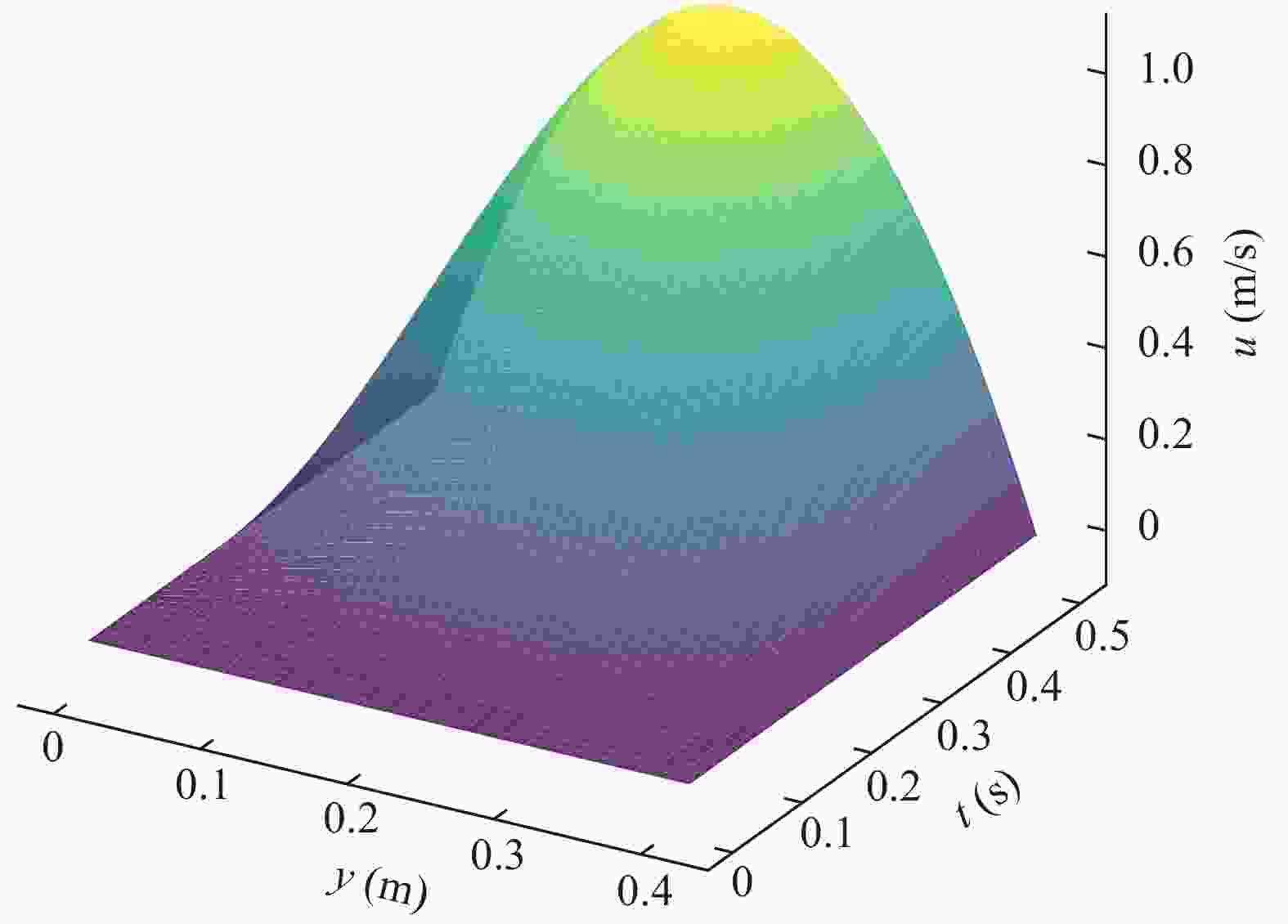
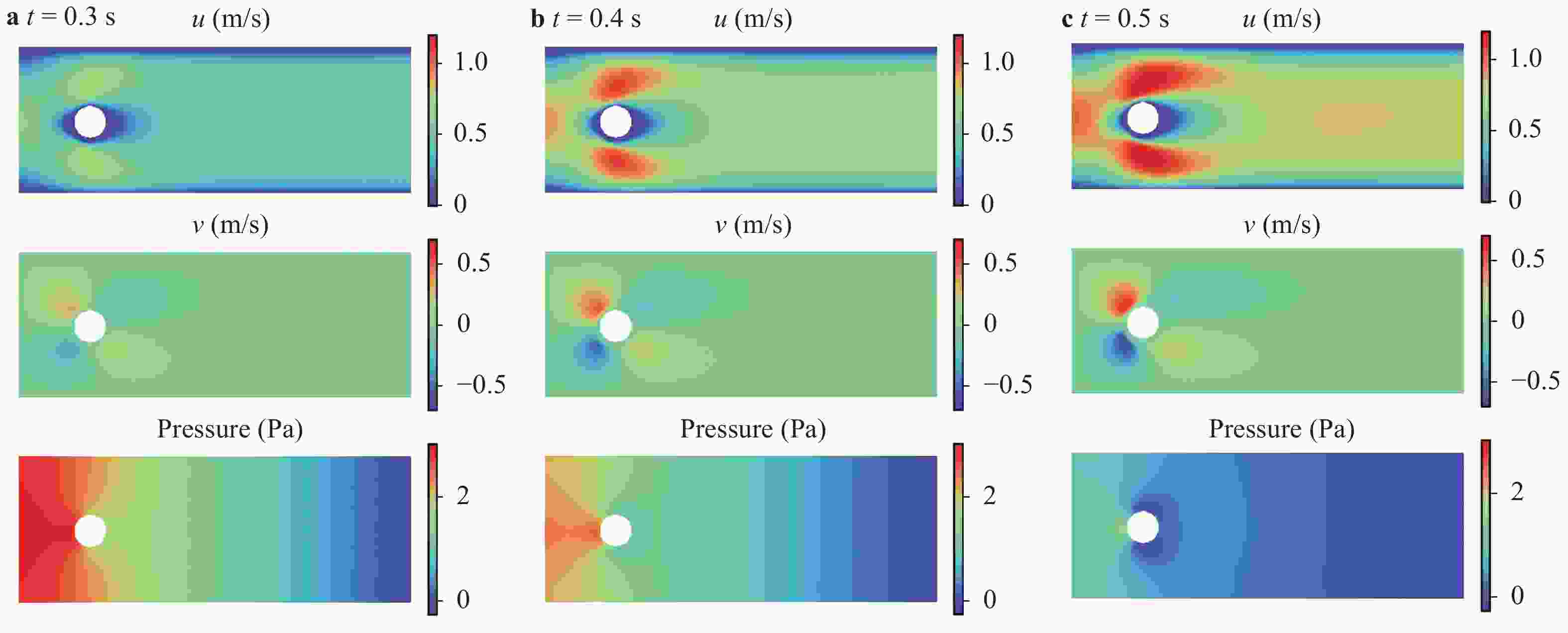
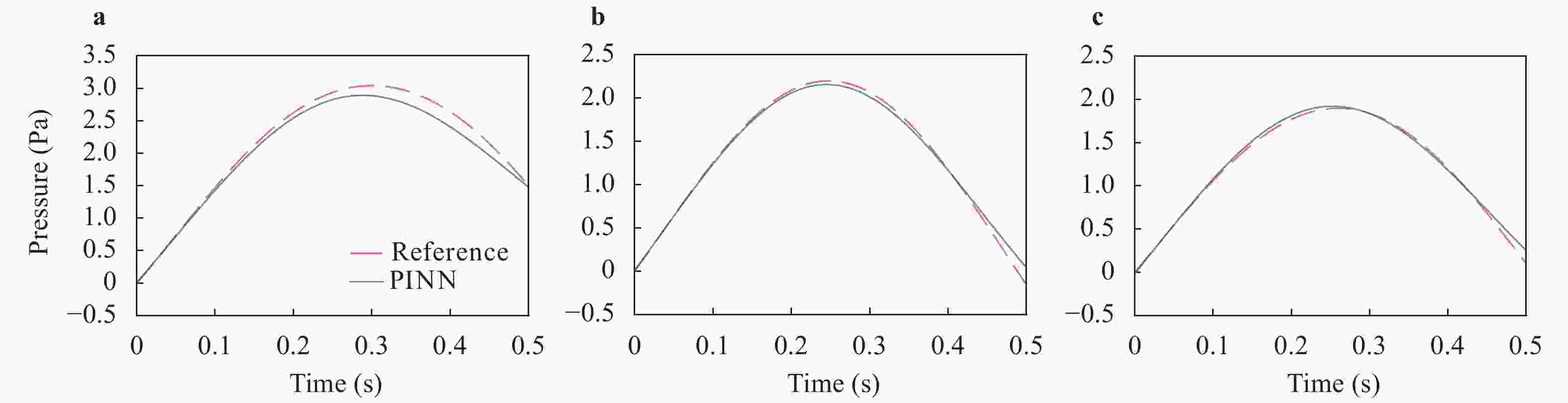
Physics-informed deep learning has drawn tremendous interest in recent years to solve computational physics problems, whose basic concept is to embed physical laws to constrain/inform neural networks, with the need of less data for training a reliable model. This can be achieved by incorporating the residual of physics equations into the loss function. Through minimizing the loss function, the network could approximate the solution. In this paper, we propose a mixed-variable scheme of physics-informed neural network (PINN) for fluid dynamics and apply it to simulate steady and transient laminar flows at low Reynolds numbers. A parametric study indicates that the mixed-variable scheme can improve the PINN trainability and the solution accuracy. The predicted velocity and pressure fields by the proposed PINN approach are also compared with the reference numerical solutions. Simulation results demonstrate great potential of the proposed PINN for fluid flow simulation with a high accuracy.
Physics-informed deep learning has drawn tremendous interest in recent years to solve computational physics problems, whose basic concept is to embed physical laws to constrain/inform neural networks, with the need of less data for training a reliable model. This can be achieved by incorporating the residual of physics equations into the loss function. Through minimizing the loss function, the network could approximate the solution. In this paper, we propose a mixed-variable scheme of physics-informed neural network (PINN) for fluid dynamics and apply it to simulate steady and transient laminar flows at low Reynolds numbers. A parametric study indicates that the mixed-variable scheme can improve the PINN trainability and the solution accuracy. The predicted velocity and pressure fields by the proposed PINN approach are also compared with the reference numerical solutions. Simulation results demonstrate great potential of the proposed PINN for fluid flow simulation with a high accuracy.
 Submit a Paper
Submit a Paper
 Subscription
Subscription
News
MORE+
Call for Papers
MORE+
- Crossing-Mechanics Driven by Big Data
- Machine learning in the fluid mechanics research of wind energy
- Mechanics of Origami/Kirigami structures and metamaterials
- New insights and perspectives on impact biomechanics for human tissues: from injury prevention, protection to protective equipment
- Environmental Mechanics for Extreme Natural Events