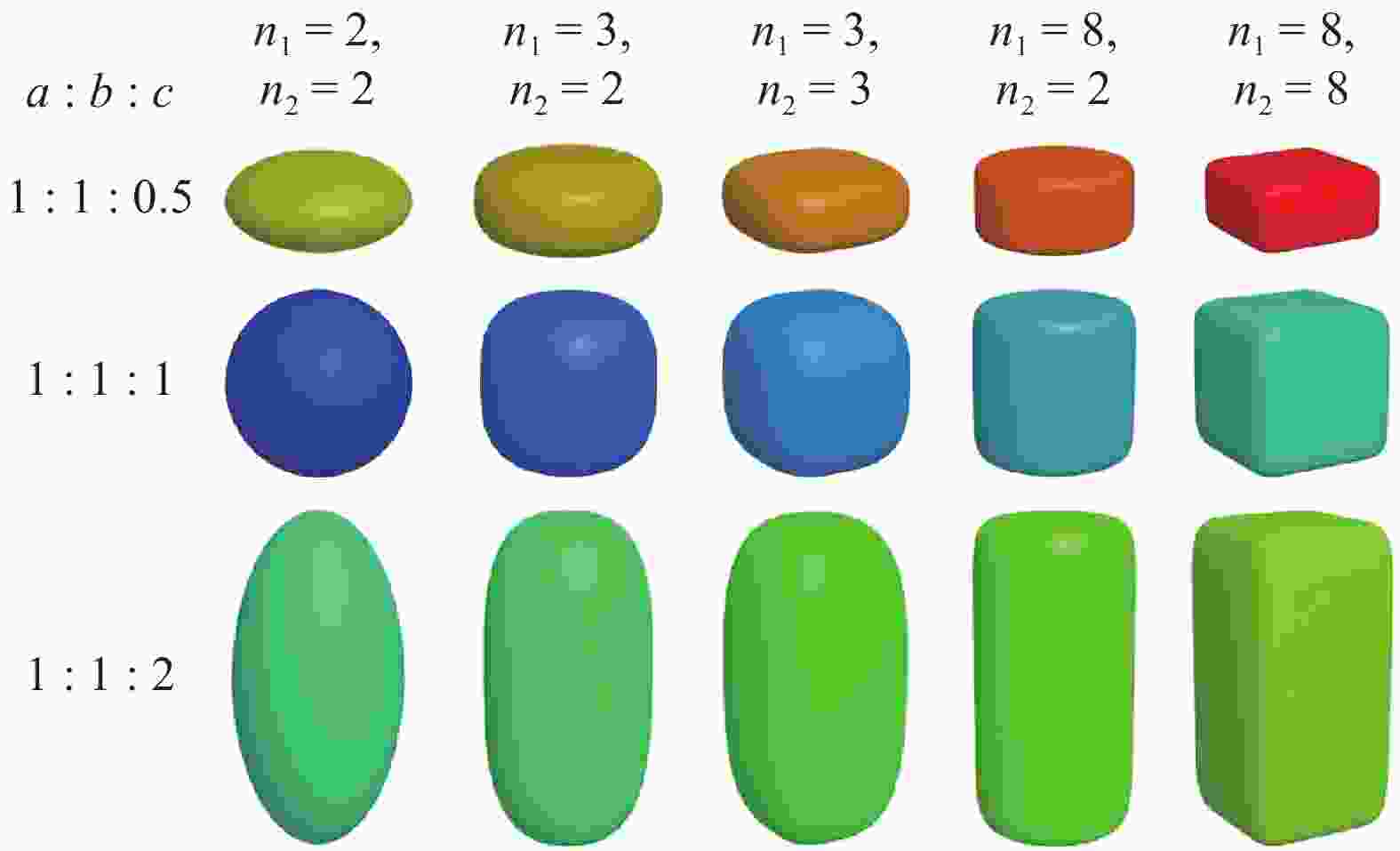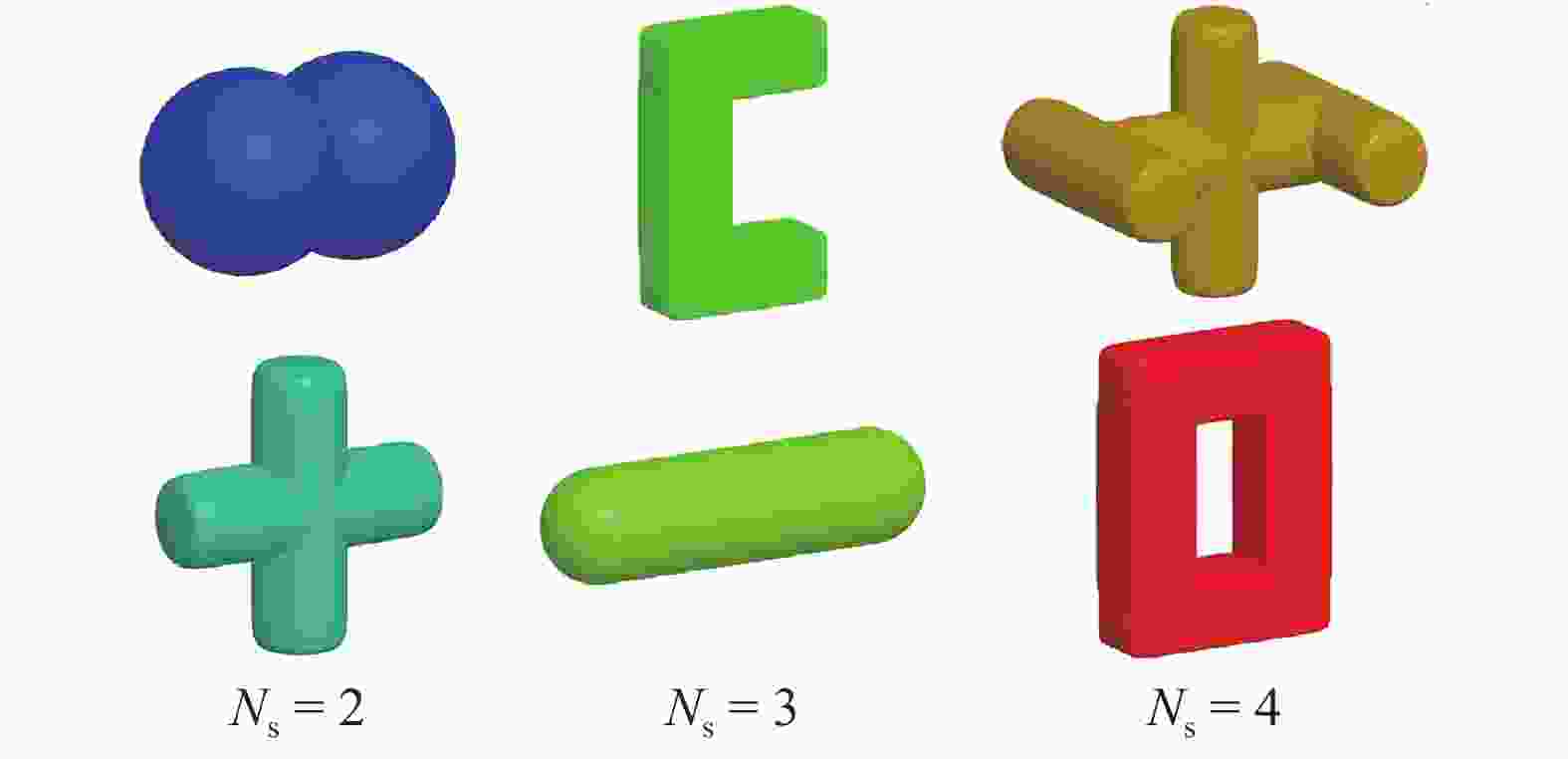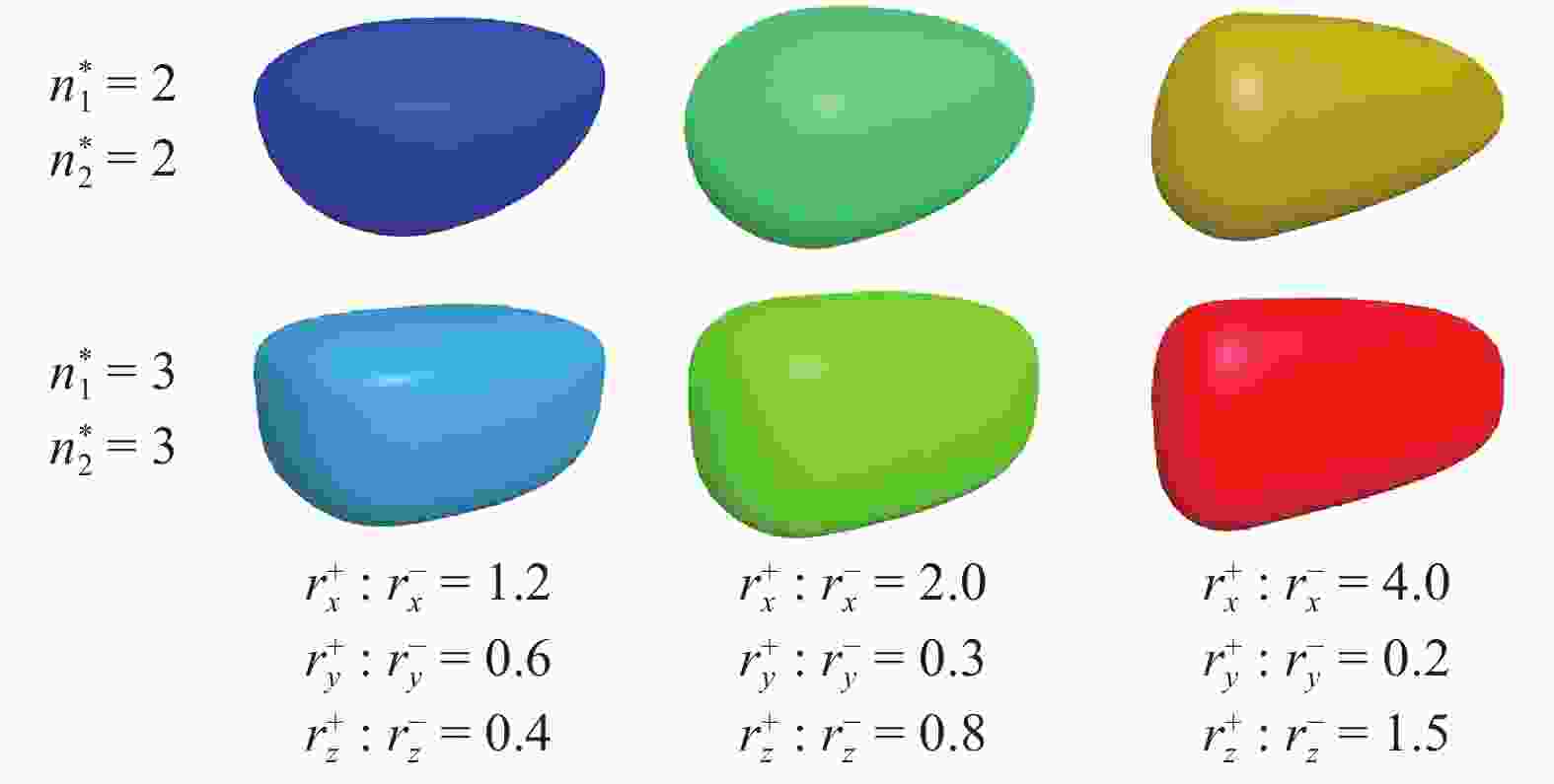Institute of Mechanics,
Chinese Academy of Sciences
2020 Vol.10(2)
Theoretical and Applied Mechanics Letters 2020, 10(2): 67-67.
doi: 10.1016/j.taml.2020.01.033
Abstract:
Theoretical and Applied Mechanics Letters 2020, 10(2): 68-73.
doi: 10.1016/j.taml.2020.01.021
Abstract:
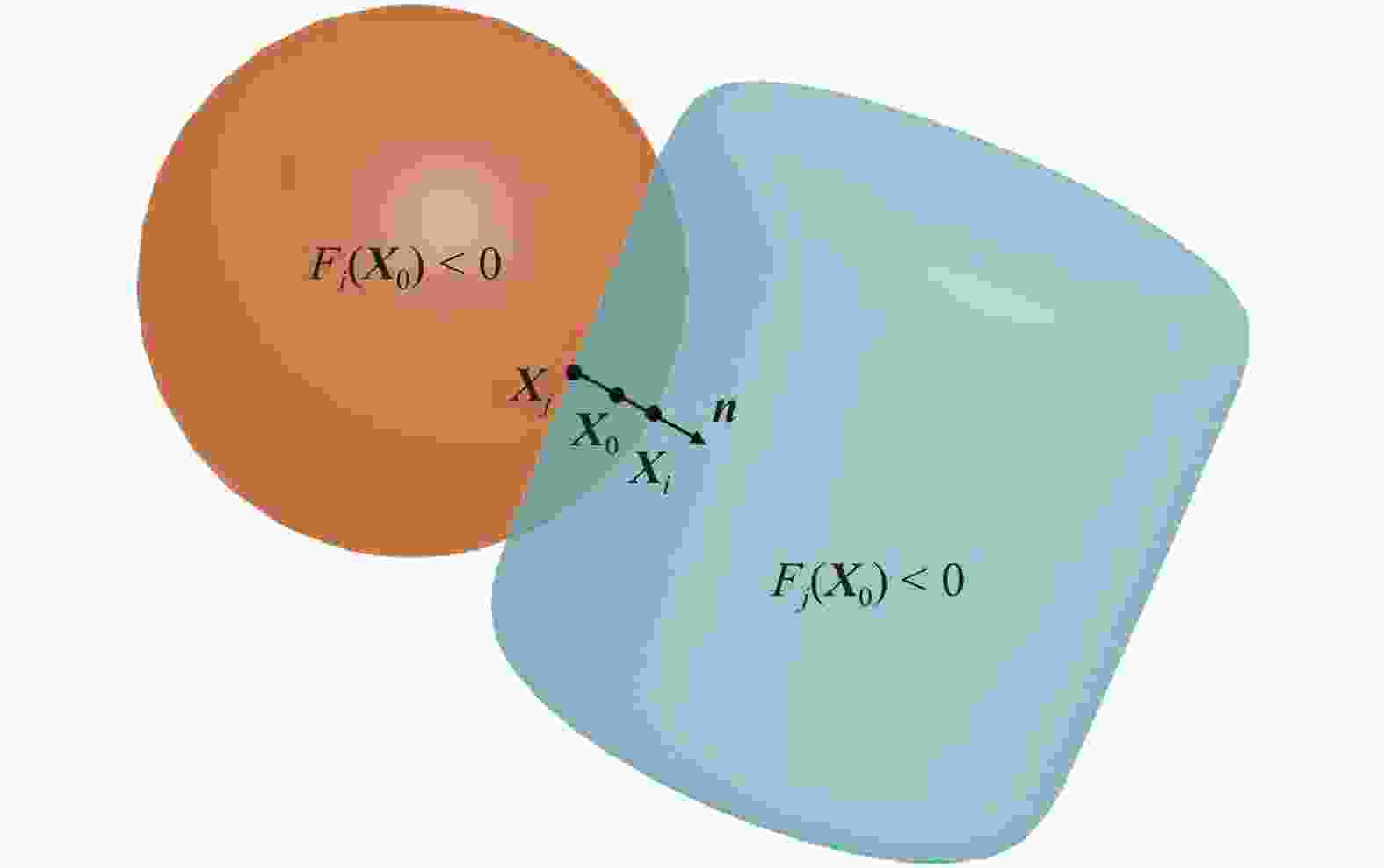
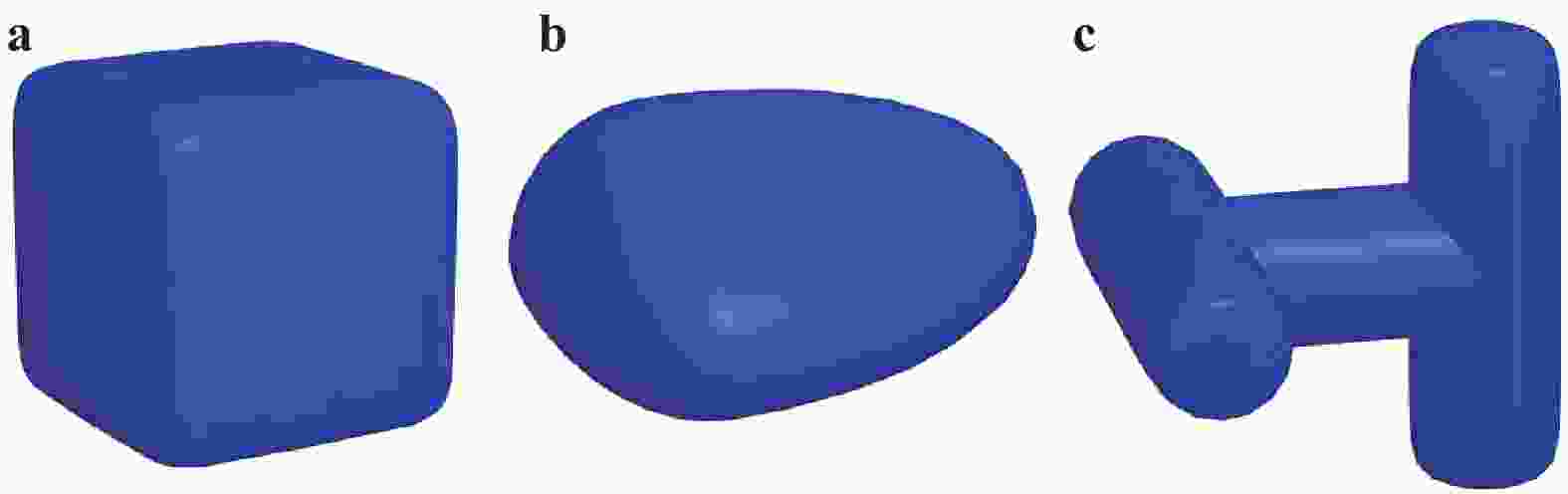
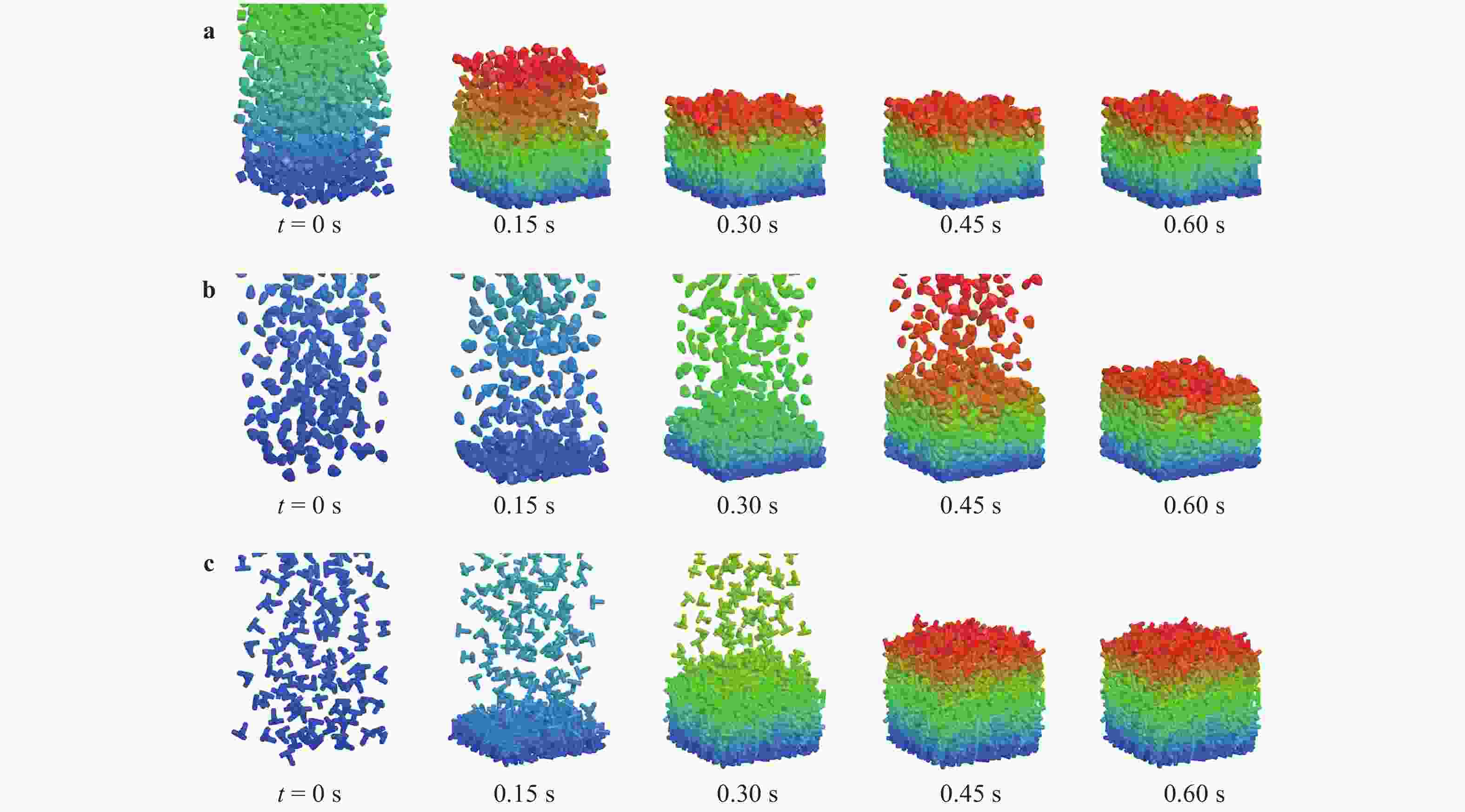
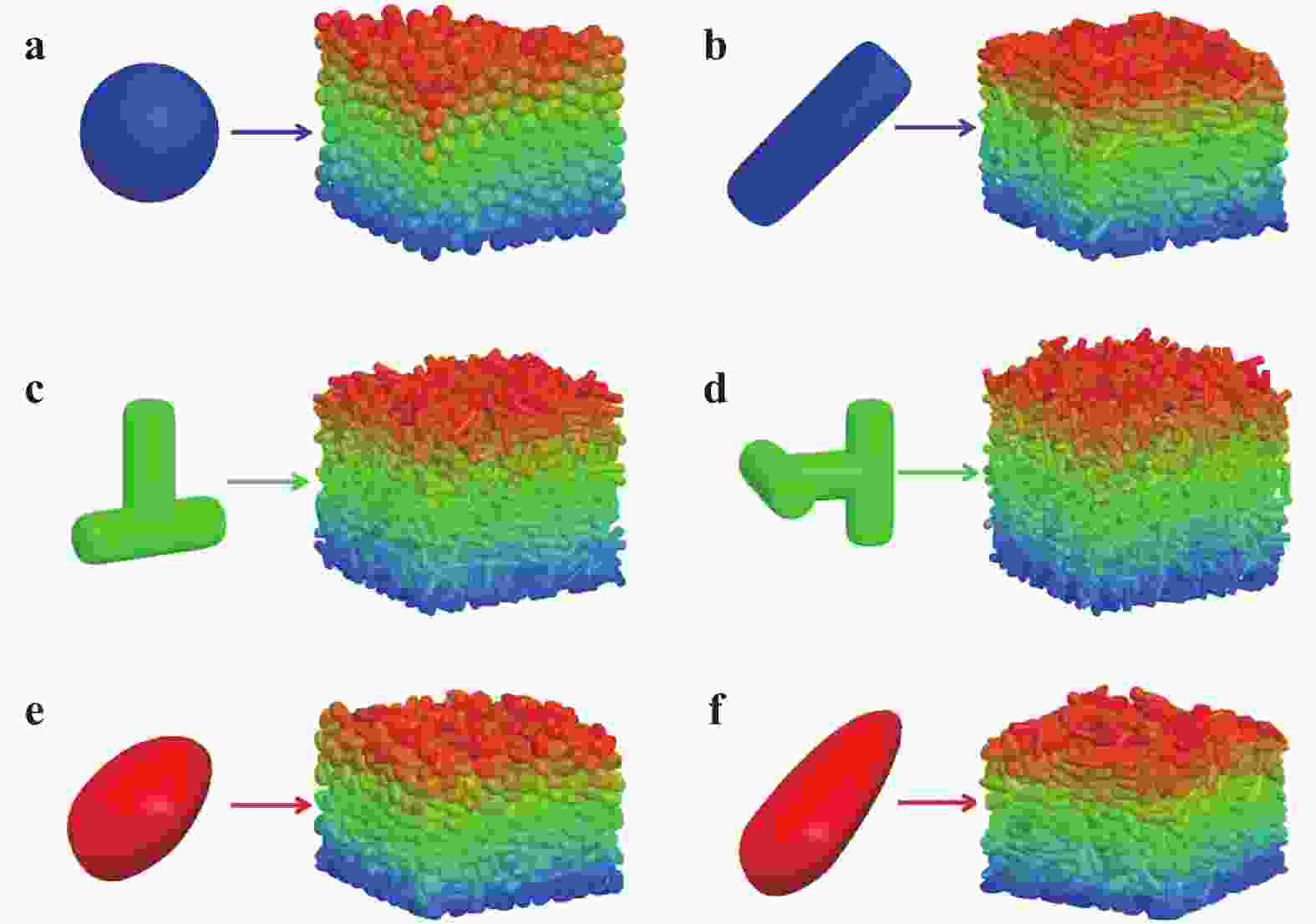
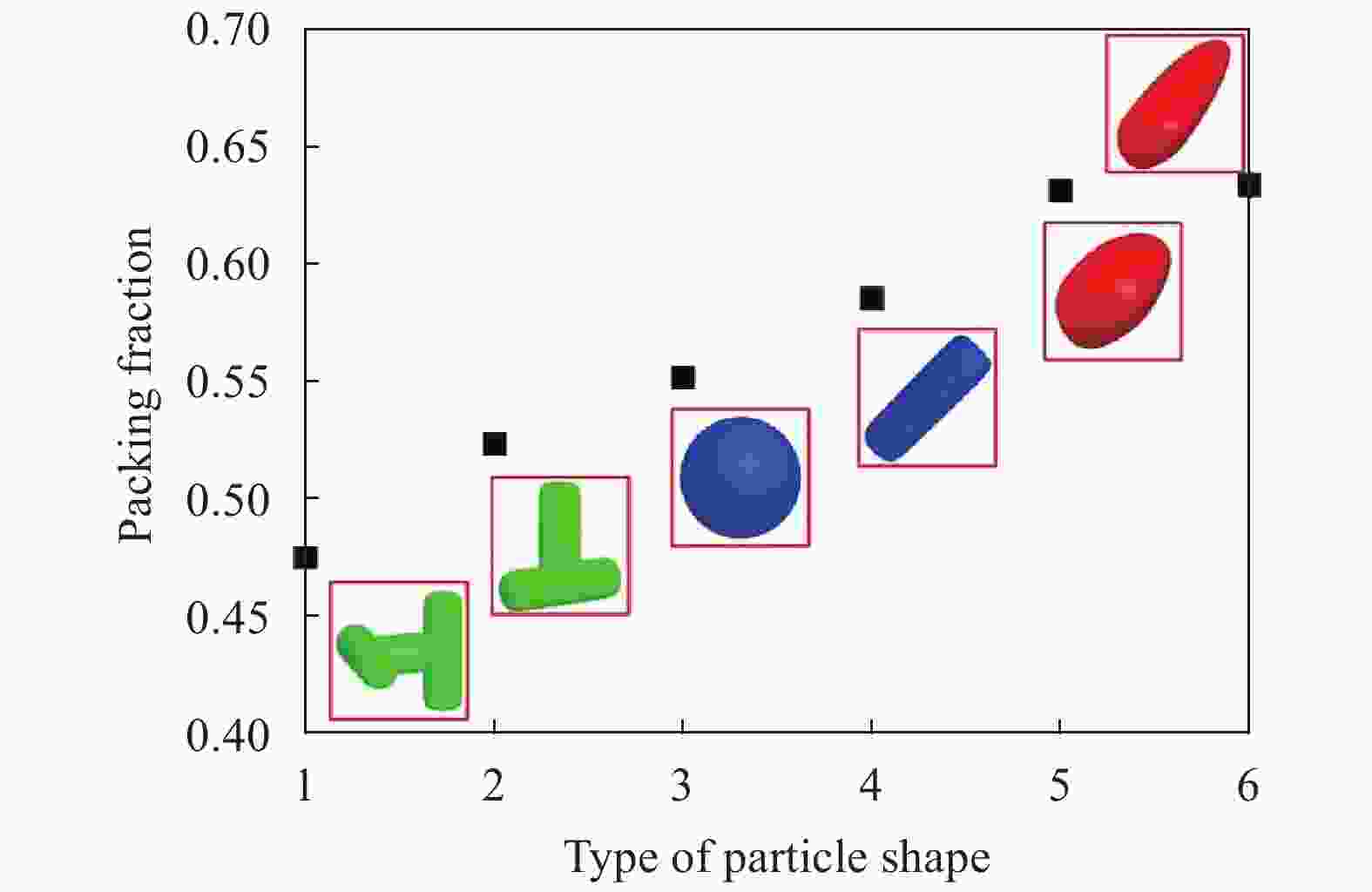
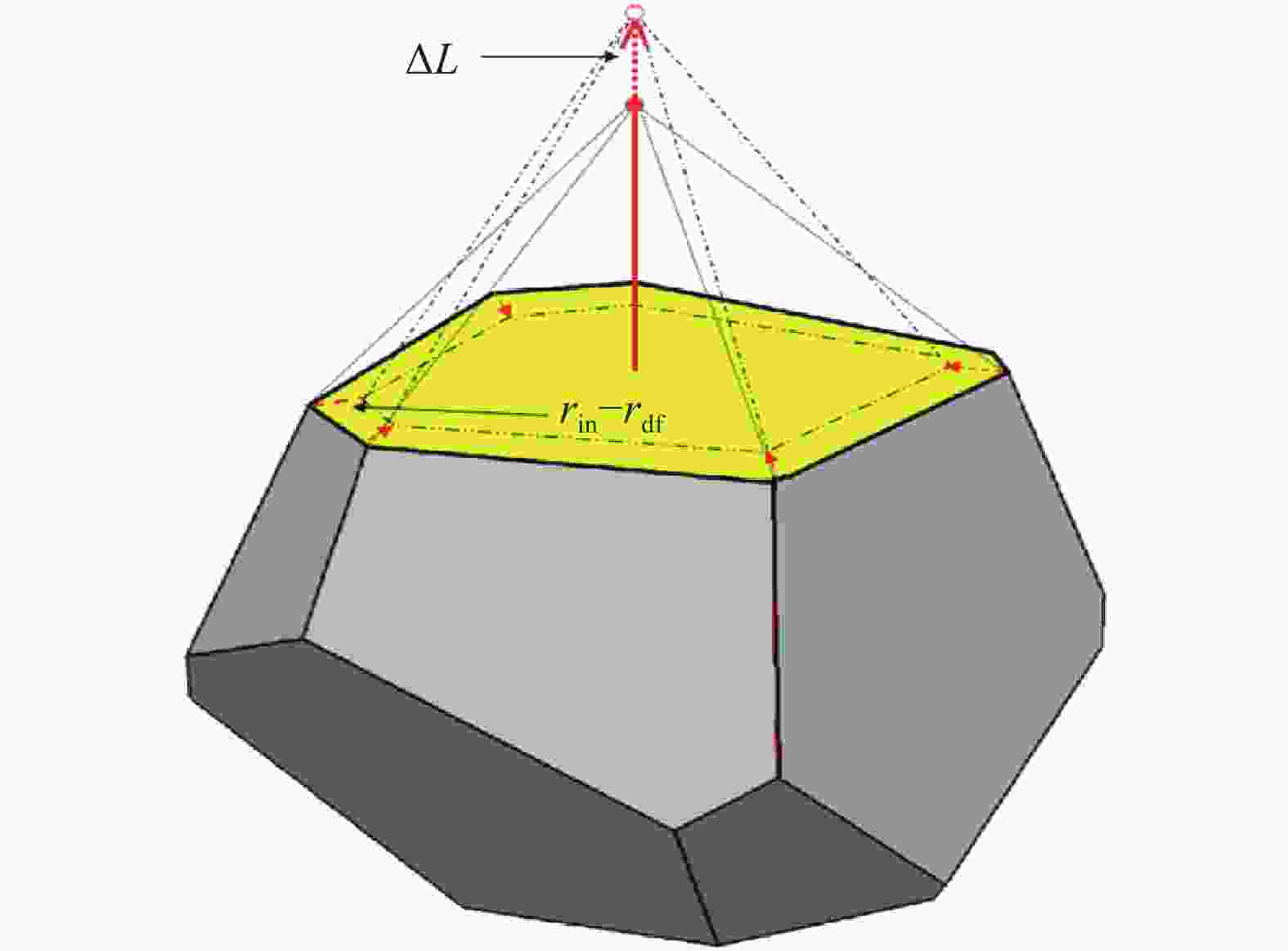
Non-spherical particles are widely present in industrial production, and significantly affect the macro and micro characteristics of granular materials. Although the superquadric equation can be used to construct non-spherical particles, its disadvantage is that the particle shape is geometrically symmetric and strictly convex. In this study, two composed approaches are used to describe geometrically asymmetric and concave particle shapes, including a multi-superquadric model and a poly-superquadric model. The multi-superquadric model is a combination of several superquadric elements, and can construct concave and geometrically asymmetric particle shapes. The poly-superquadric model is a combination of eight one-eighth superquadric elements, and can construct convex and geometrically asymmetric particle shapes. Both composed models are based on superquadric equations, and Newton's iterative method is used to calculate the contact force between the elements. Furthermore, superquadric elements, multi-superquadric elements, and poly-superquadric elements are applied for the formation of complex granular beds, and the influences of particle shape on the packing fraction can be successfully captured by the proposed models.
Non-spherical particles are widely present in industrial production, and significantly affect the macro and micro characteristics of granular materials. Although the superquadric equation can be used to construct non-spherical particles, its disadvantage is that the particle shape is geometrically symmetric and strictly convex. In this study, two composed approaches are used to describe geometrically asymmetric and concave particle shapes, including a multi-superquadric model and a poly-superquadric model. The multi-superquadric model is a combination of several superquadric elements, and can construct concave and geometrically asymmetric particle shapes. The poly-superquadric model is a combination of eight one-eighth superquadric elements, and can construct convex and geometrically asymmetric particle shapes. Both composed models are based on superquadric equations, and Newton's iterative method is used to calculate the contact force between the elements. Furthermore, superquadric elements, multi-superquadric elements, and poly-superquadric elements are applied for the formation of complex granular beds, and the influences of particle shape on the packing fraction can be successfully captured by the proposed models.
Theoretical and Applied Mechanics Letters 2020, 10(2): 74-78.
doi: 10.1016/j.taml.2020.01.007
Abstract:
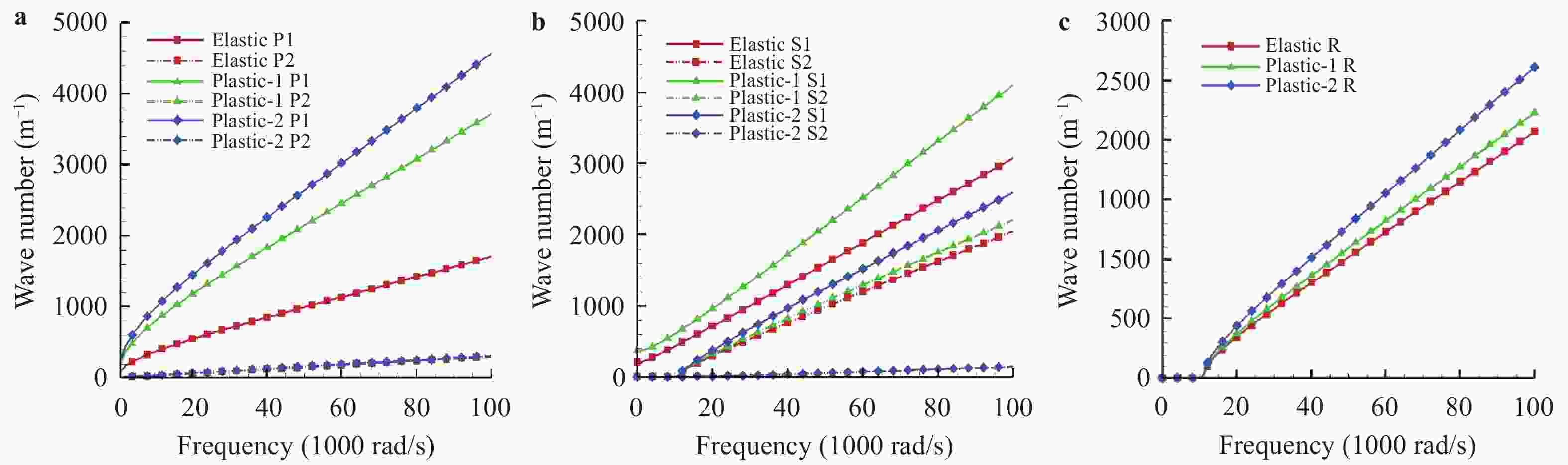
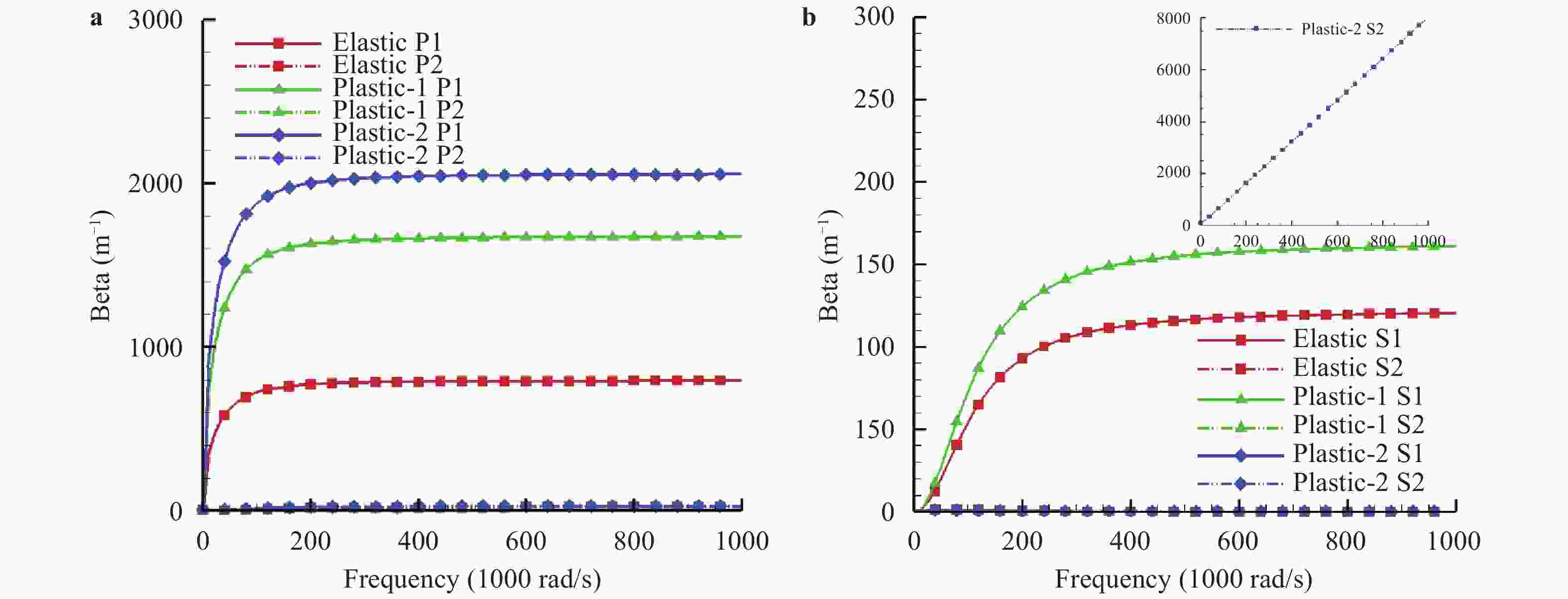
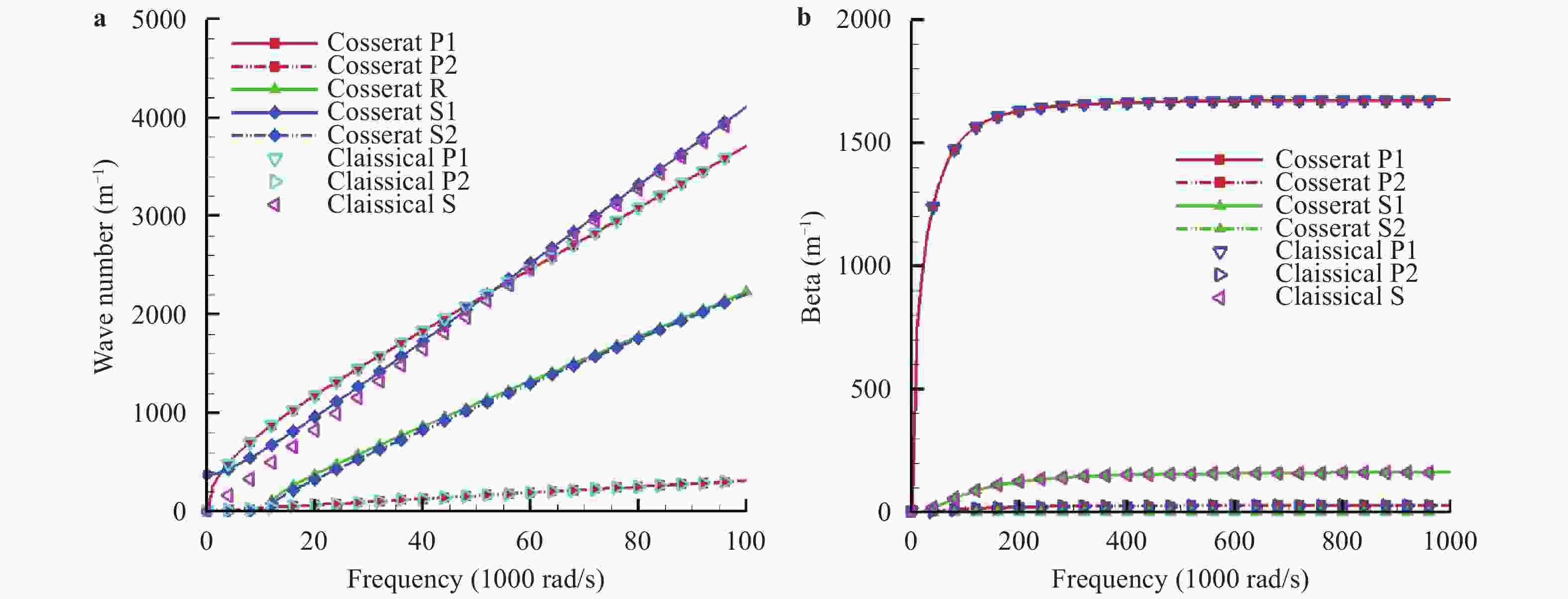
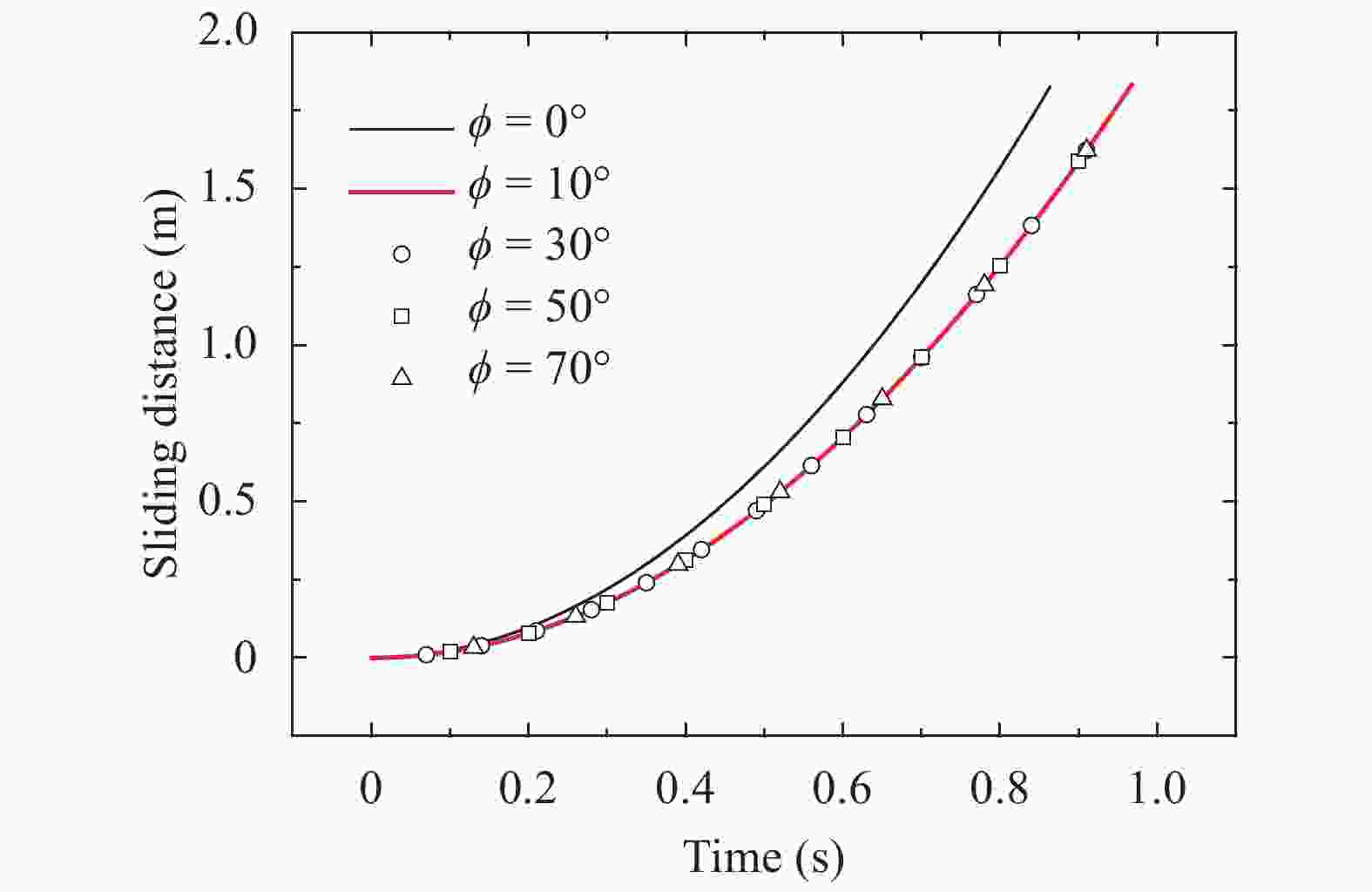
This study focuses on the propagation of the plane wave in the elastoplastic unsaturated granular media, and the wave equations and dispersion equations are derived for the media under the framework of Cosserat theory. Due to symmetry, five different wave modes are considered and predicted for the elastoplastic unsaturated granular media based on the Cosserat theory, including two longitudinal waves, one rotational longitudinal wave and two coupled transverse–rotational transverse waves. The correspondence is discussed between these Cosserat wave modes and the classical wave modes. Based on the dispersion equations, the dispersion behaviors are obtained for the five Cosserat wave modes. The results indicated that the different stress-strain stages, including the elastic, hardening and softening stages, have obvious effect on the dispersion behaviors of the Cosserat wave modes.
This study focuses on the propagation of the plane wave in the elastoplastic unsaturated granular media, and the wave equations and dispersion equations are derived for the media under the framework of Cosserat theory. Due to symmetry, five different wave modes are considered and predicted for the elastoplastic unsaturated granular media based on the Cosserat theory, including two longitudinal waves, one rotational longitudinal wave and two coupled transverse–rotational transverse waves. The correspondence is discussed between these Cosserat wave modes and the classical wave modes. Based on the dispersion equations, the dispersion behaviors are obtained for the five Cosserat wave modes. The results indicated that the different stress-strain stages, including the elastic, hardening and softening stages, have obvious effect on the dispersion behaviors of the Cosserat wave modes.
Theoretical and Applied Mechanics Letters 2020, 10(2): 79-86.
doi: 10.1016/j.taml.2020.01.022
Abstract:
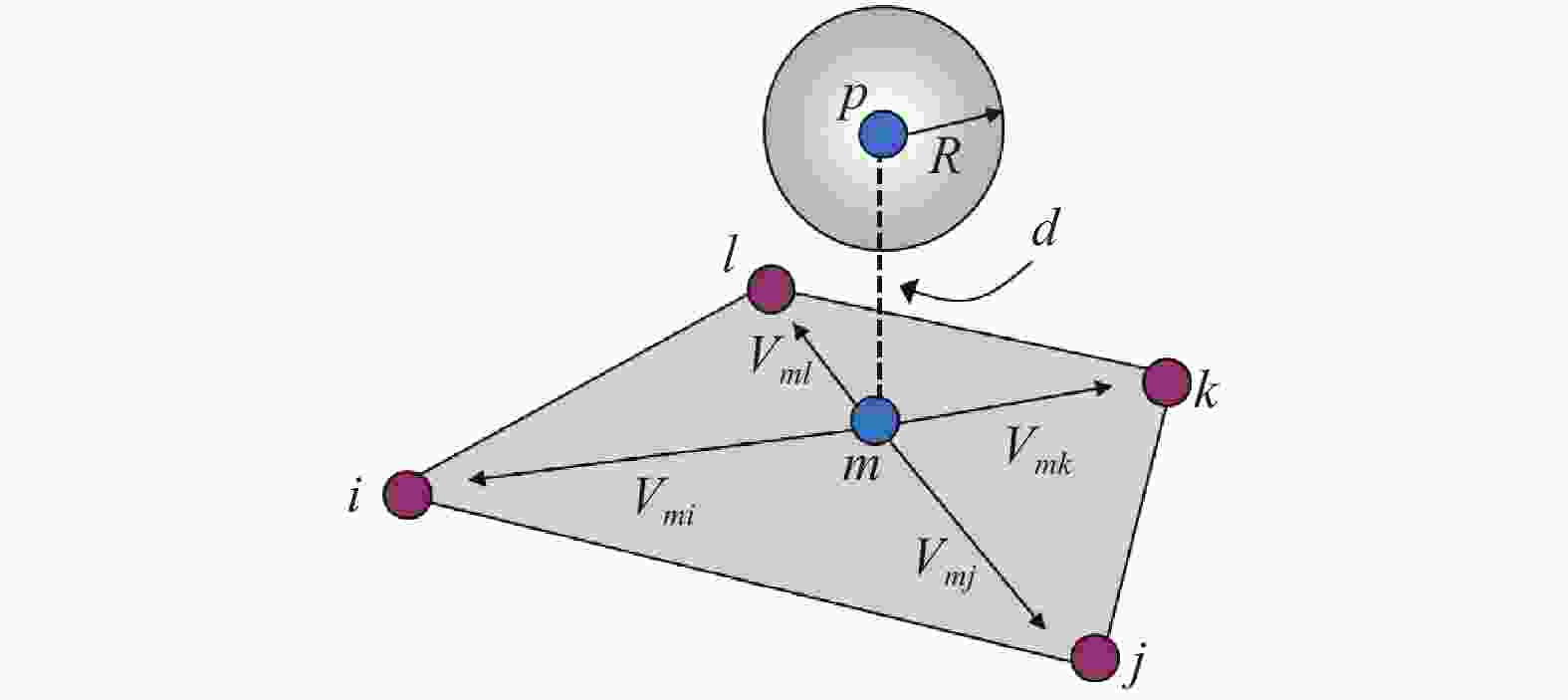
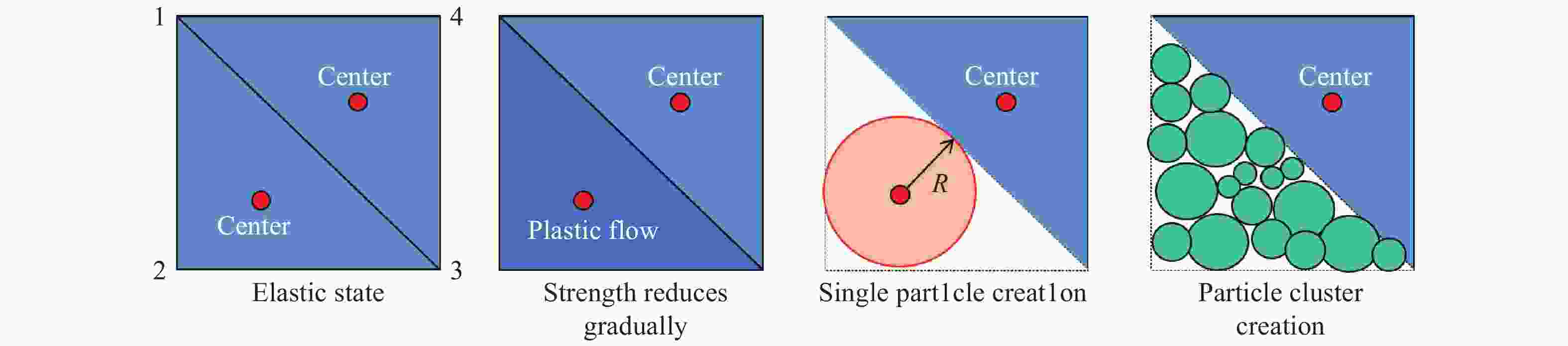
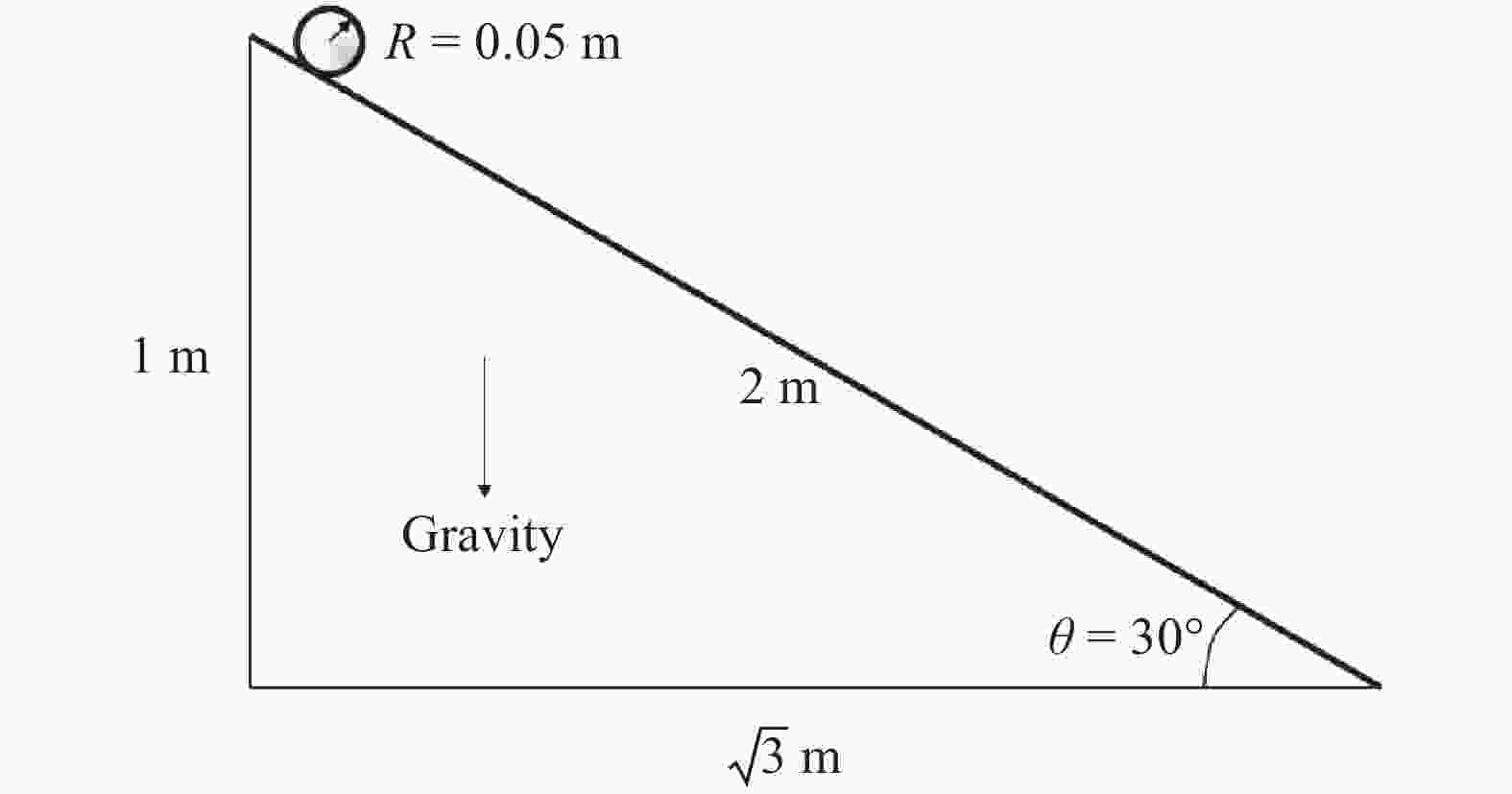
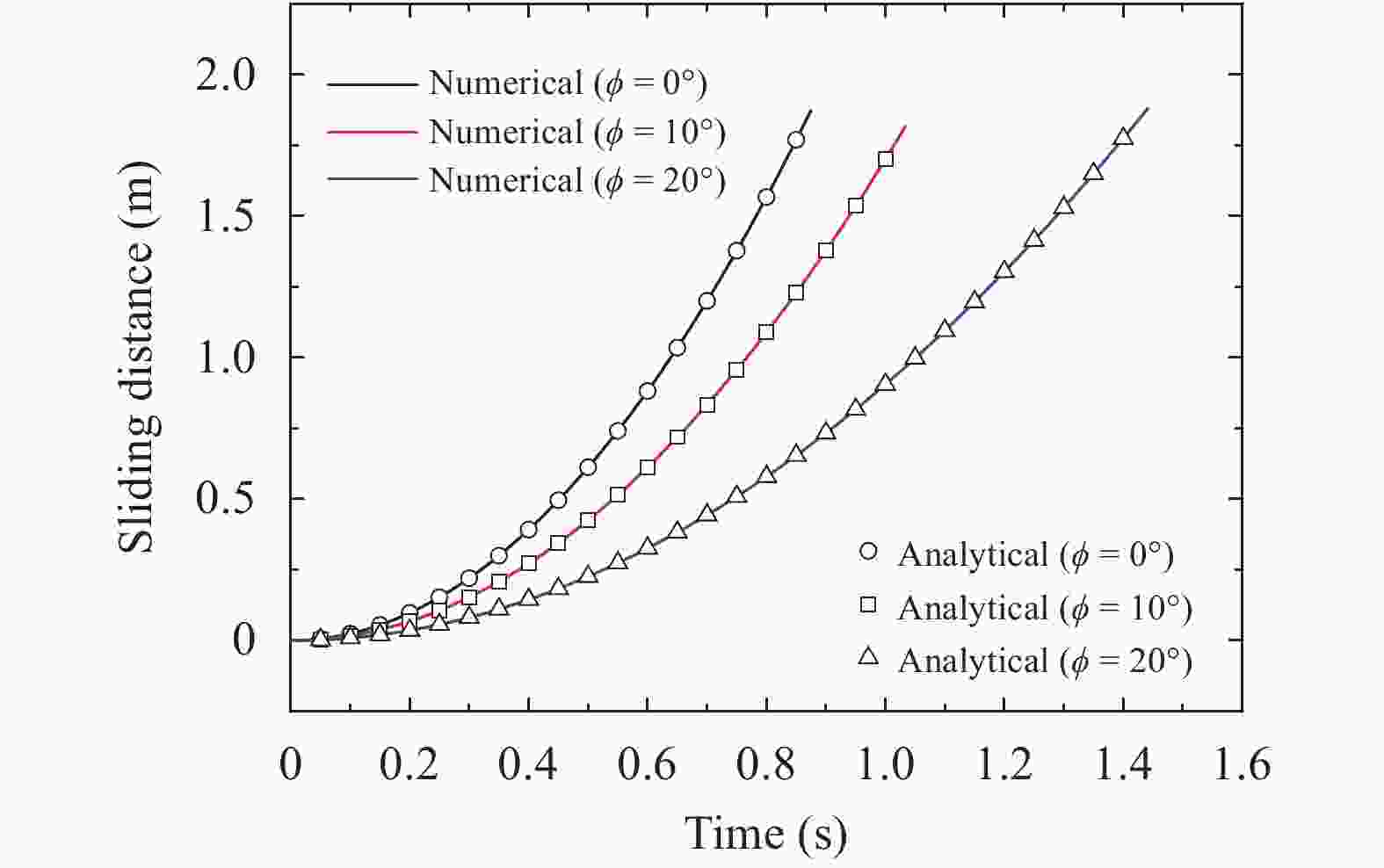
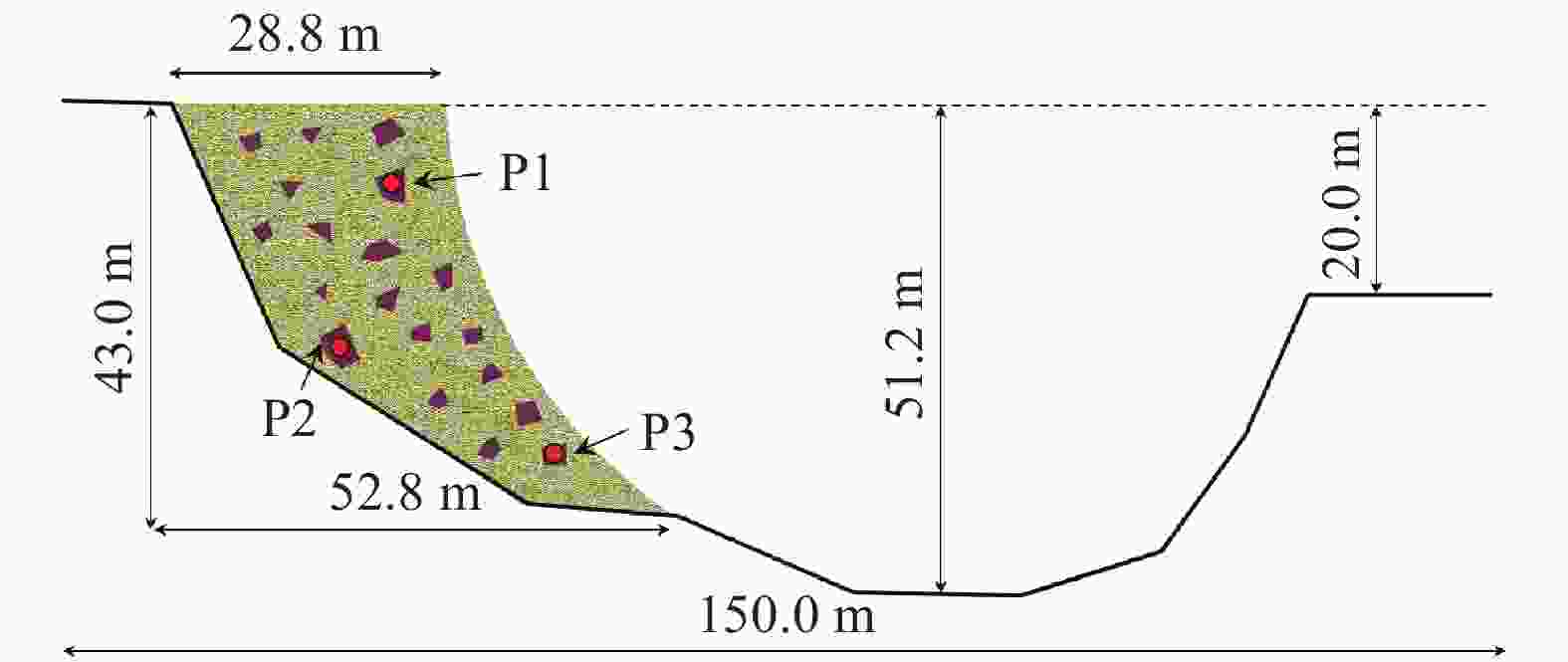
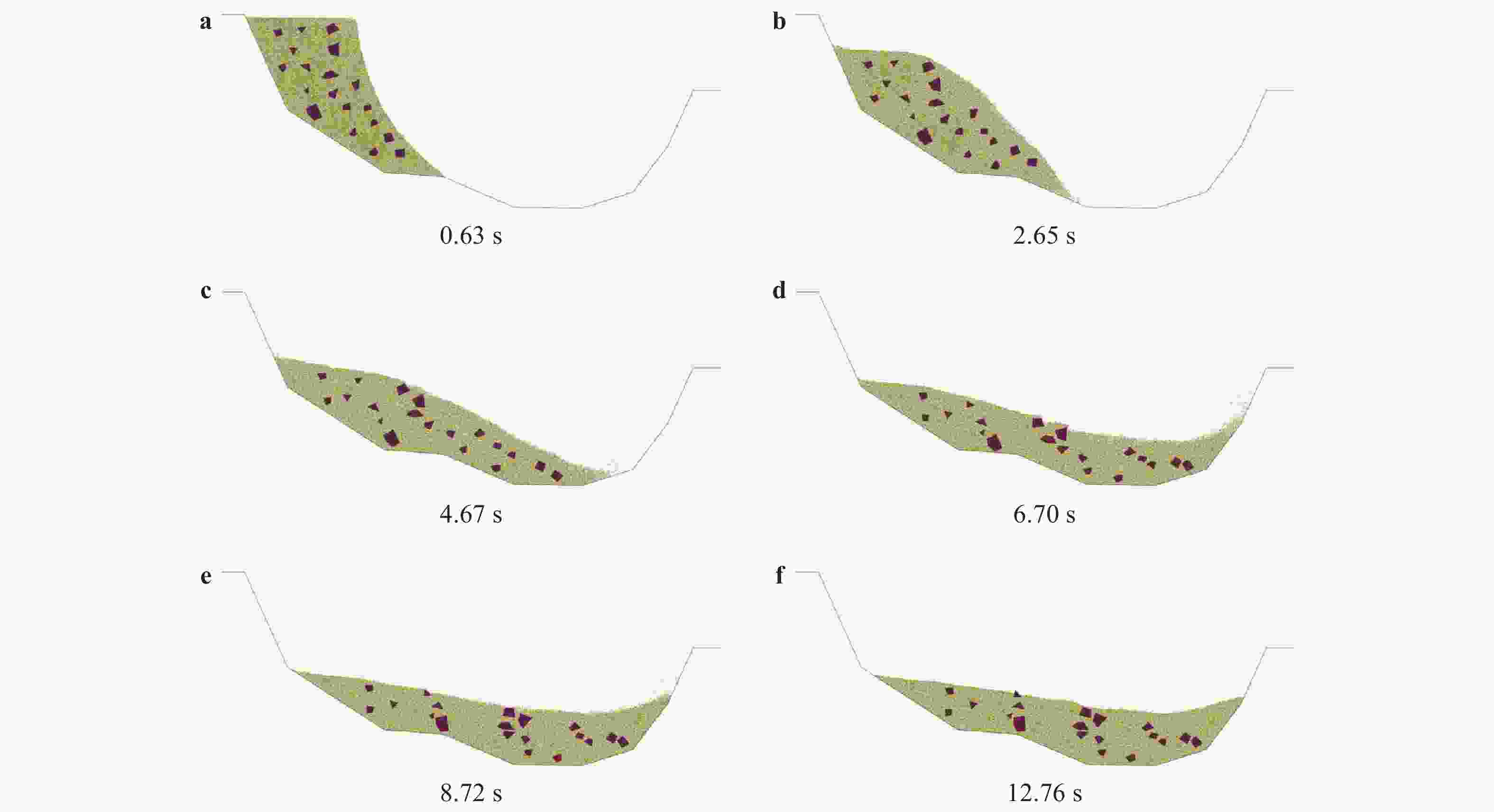
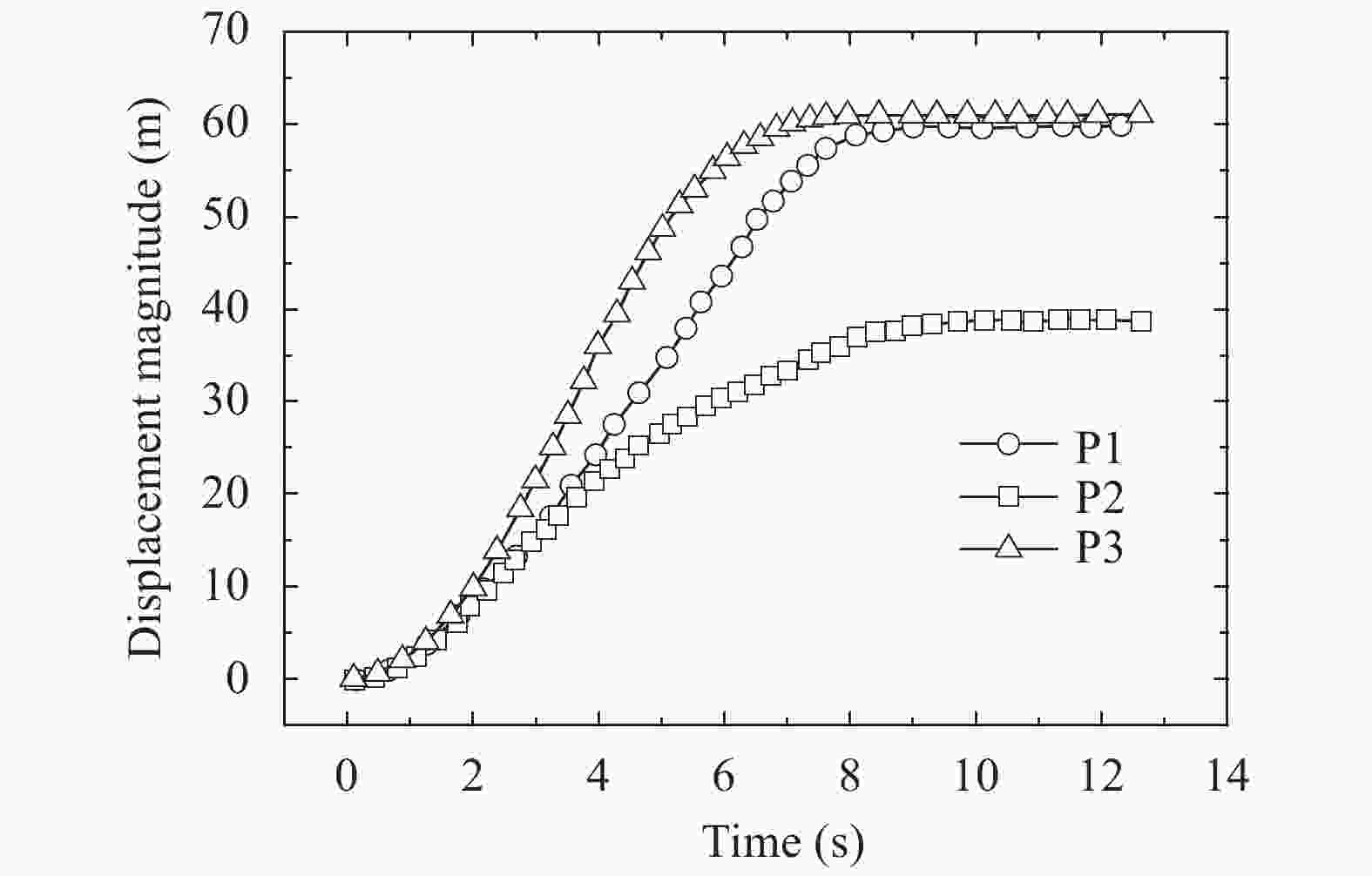
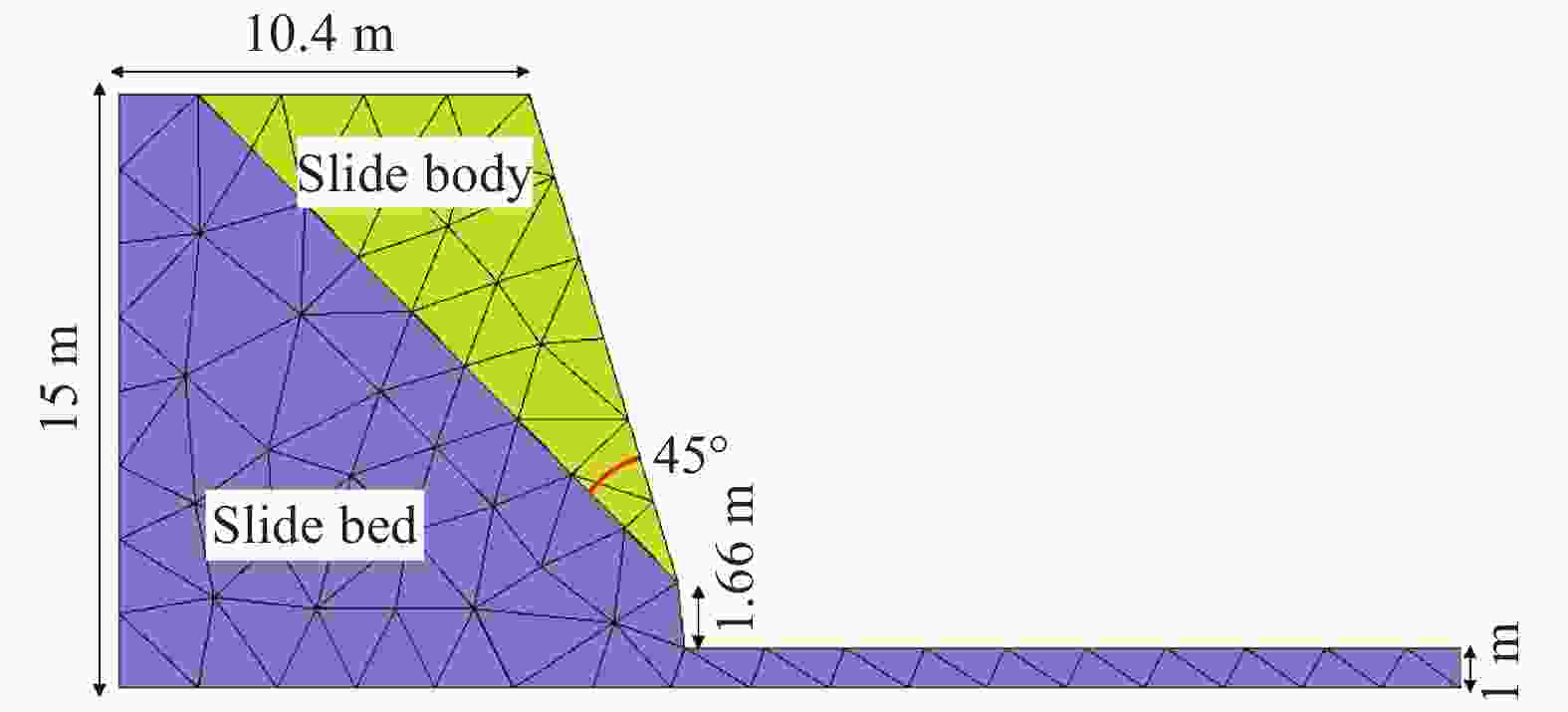
To simulate the progressive failure of slope, a block particle coupled model is introduced. Particle oriented cell mapping (POCM) algorithm is used to enhance the search efficiency, and particle-point, particle-edge, particle-face contact detecting method is adopted to establish contact pair between particles and blocks precisely. Strain softening Mohr Coulomb model with tensile cutoff is adopted for blocks, and brittle Mohr Coulomb model is used for particles. The particle-block replacement approach is used to describe the fracture and fragmentation process of continuum media. Once the cohesion or tensile strength of one block reaches zero, the block will be deleted, and particles are generated at the same place with all information inherited from the deleted block. Some numerical cases related to landslides demonstrate the precision and rationality of the coupled model.
To simulate the progressive failure of slope, a block particle coupled model is introduced. Particle oriented cell mapping (POCM) algorithm is used to enhance the search efficiency, and particle-point, particle-edge, particle-face contact detecting method is adopted to establish contact pair between particles and blocks precisely. Strain softening Mohr Coulomb model with tensile cutoff is adopted for blocks, and brittle Mohr Coulomb model is used for particles. The particle-block replacement approach is used to describe the fracture and fragmentation process of continuum media. Once the cohesion or tensile strength of one block reaches zero, the block will be deleted, and particles are generated at the same place with all information inherited from the deleted block. Some numerical cases related to landslides demonstrate the precision and rationality of the coupled model.
Theoretical and Applied Mechanics Letters 2020, 10(2): 87-91.
doi: 10.1016/j.taml.2020.01.008
Abstract:
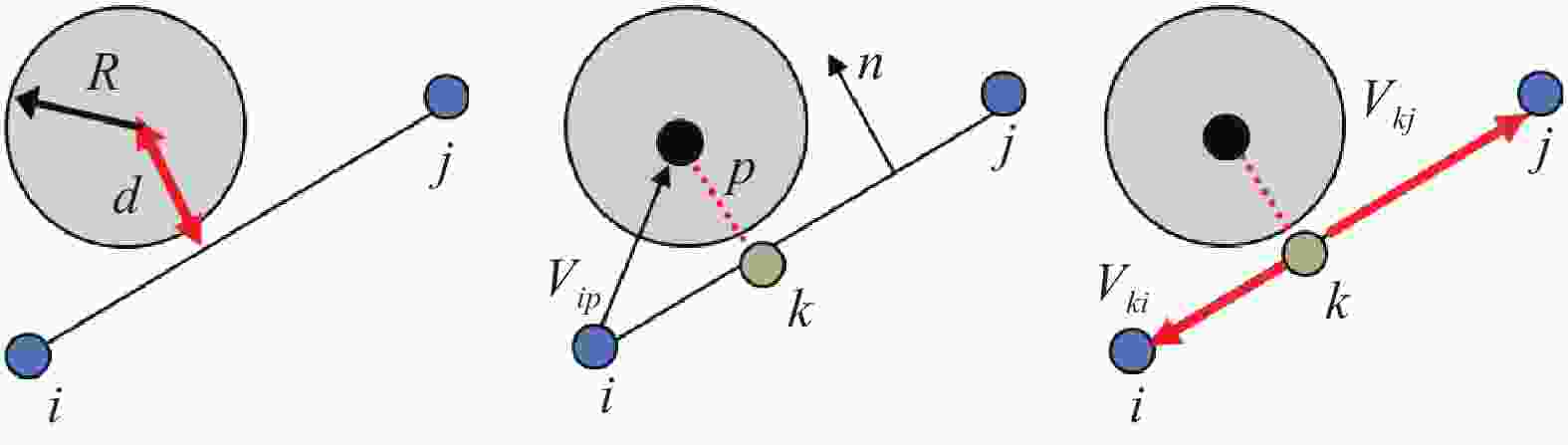
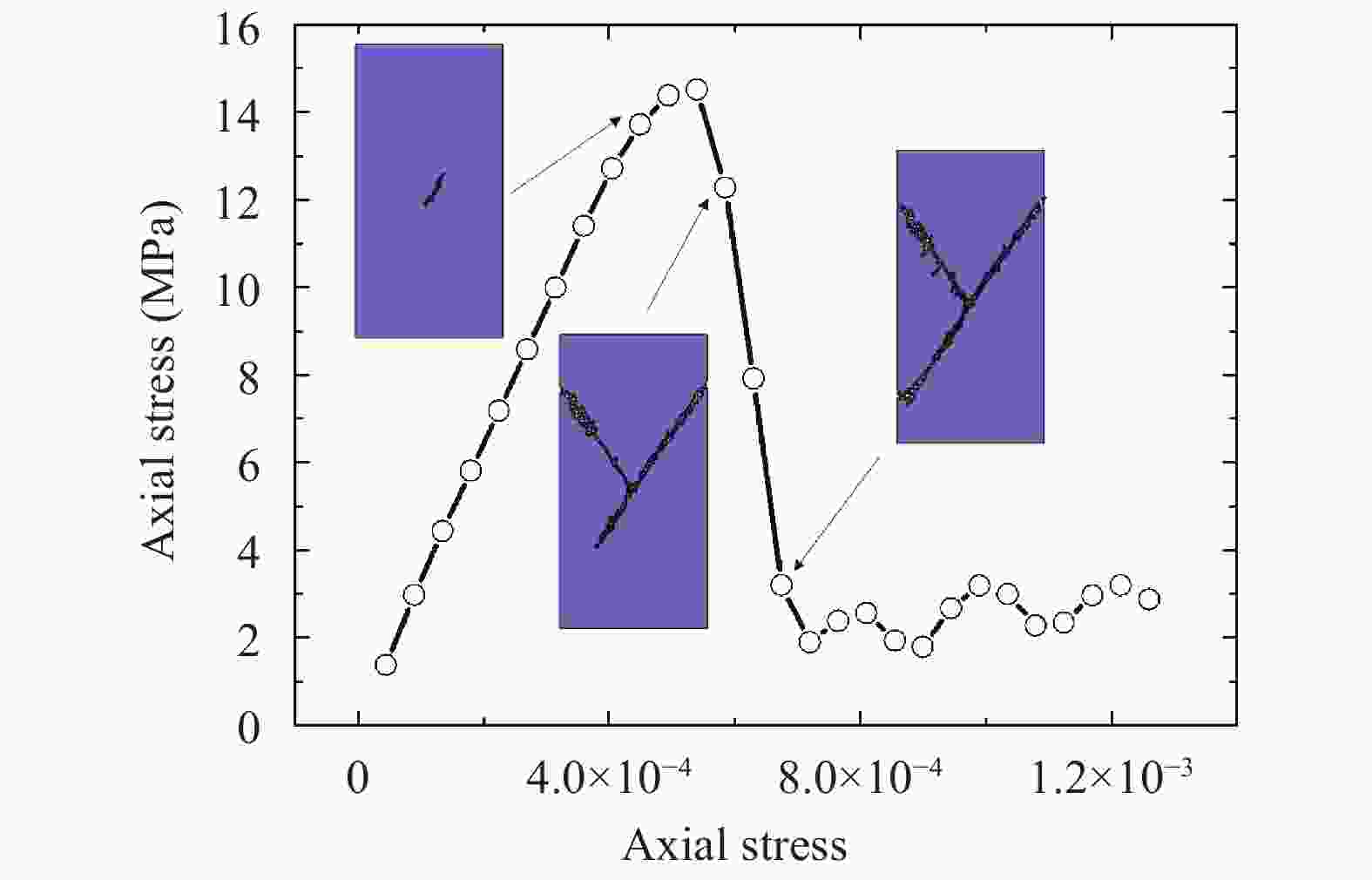
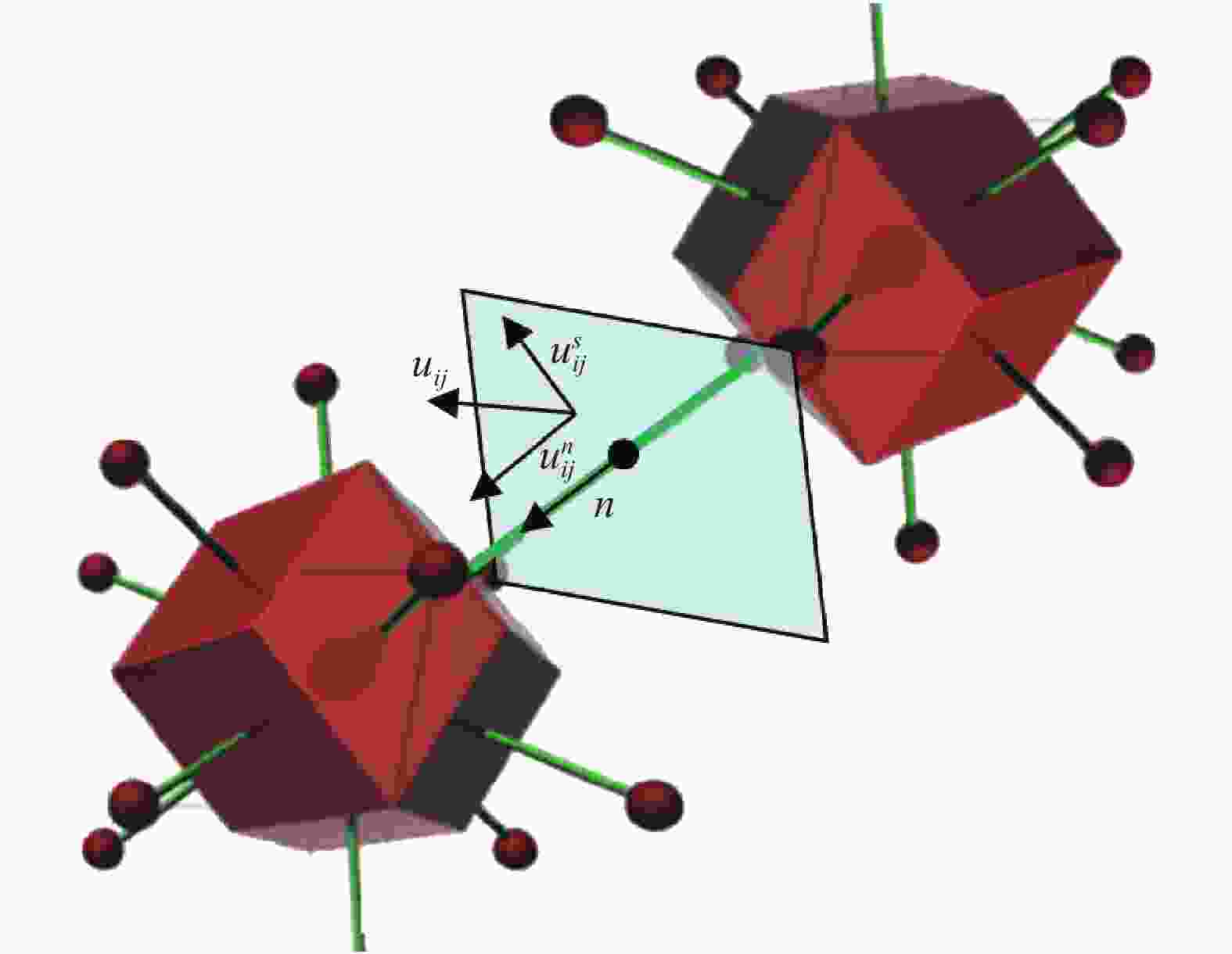
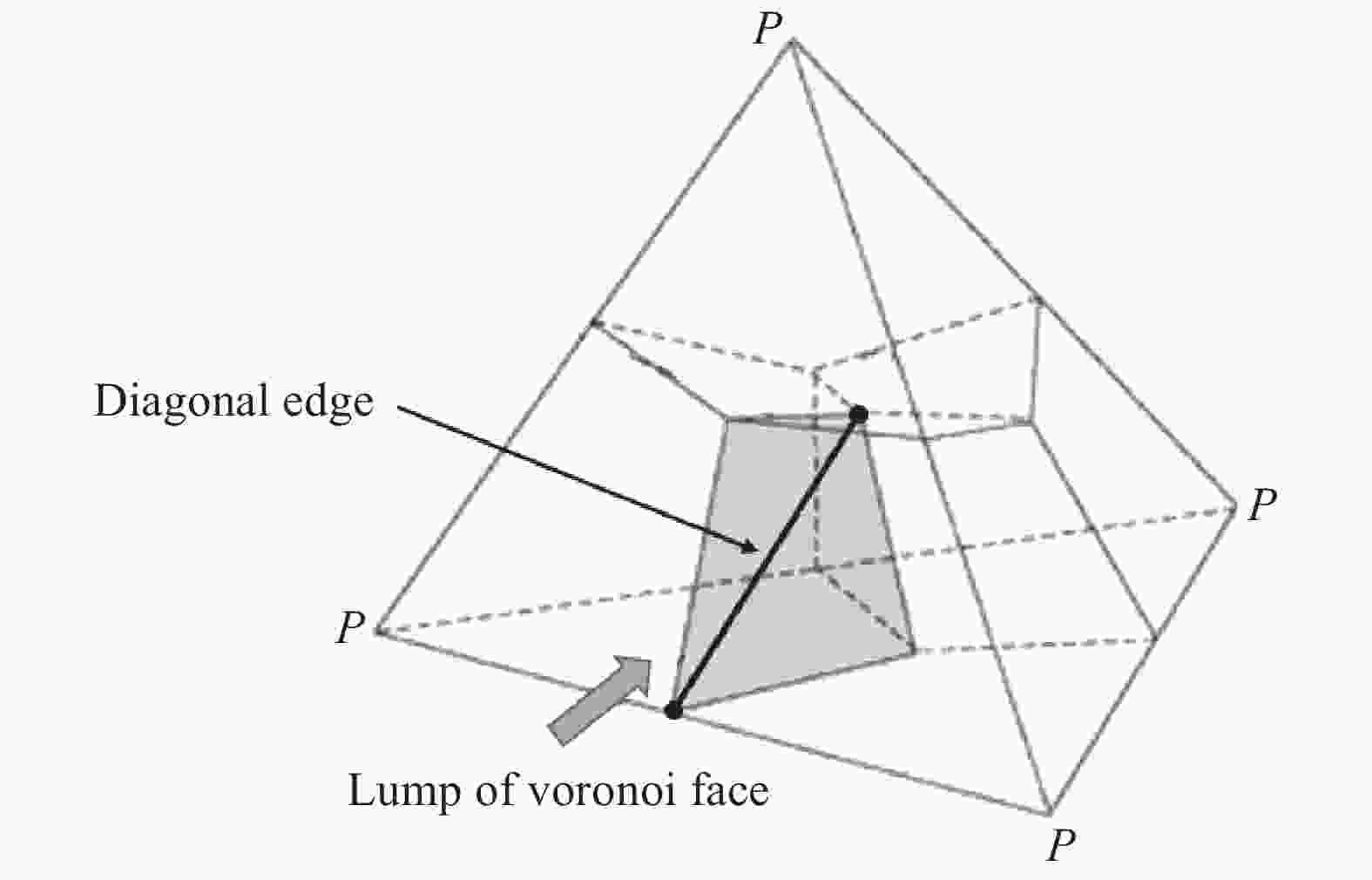
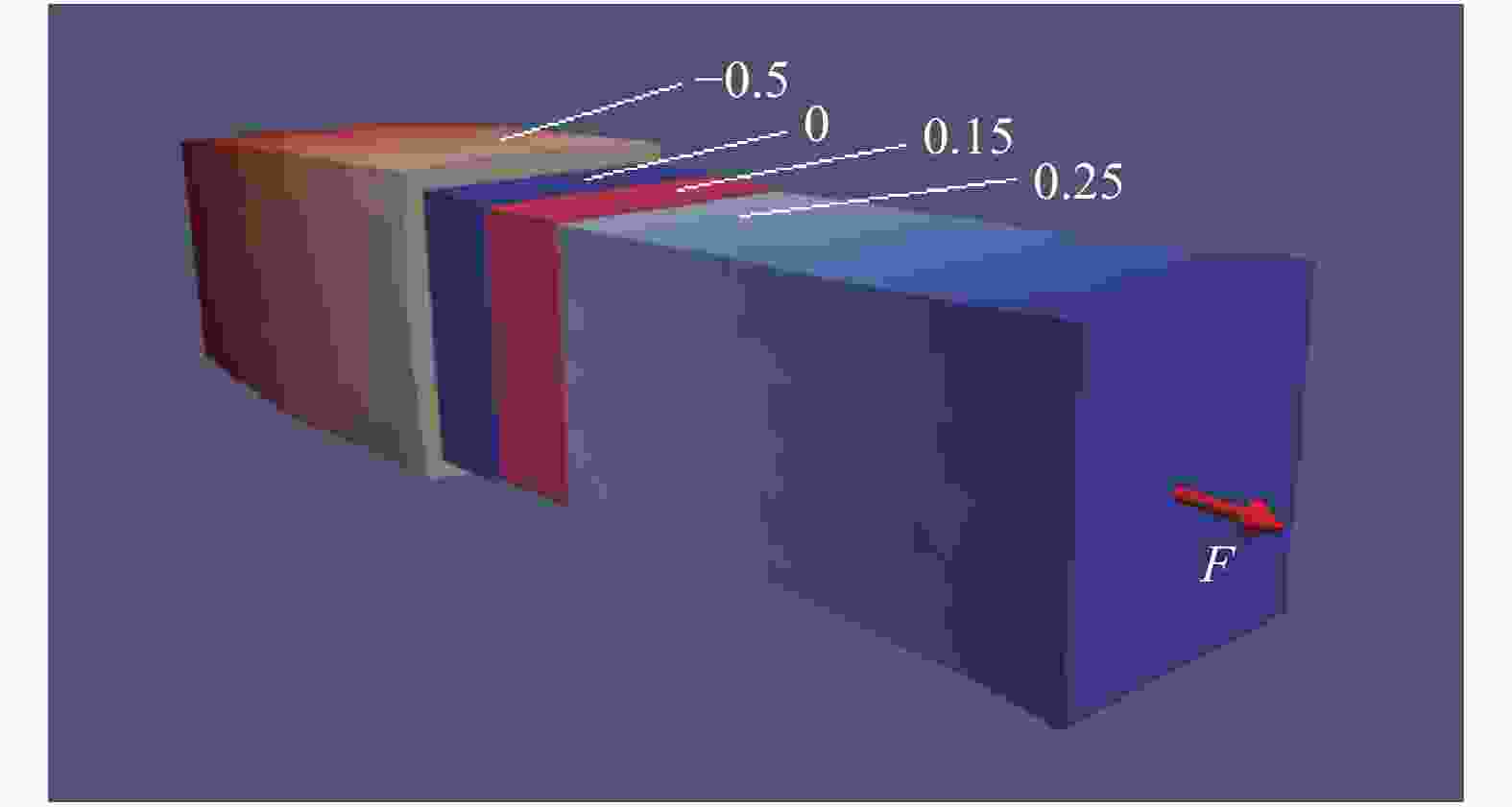
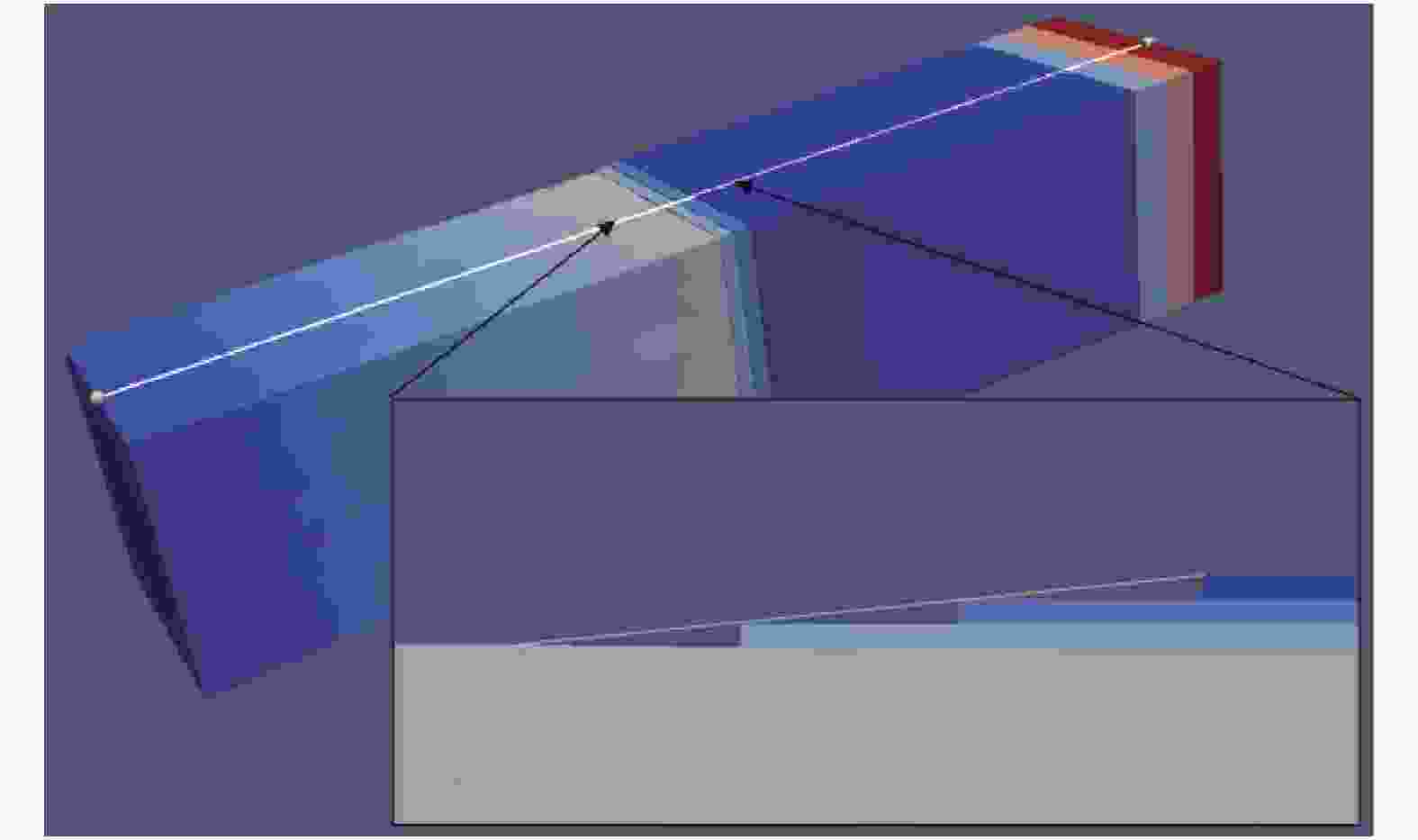
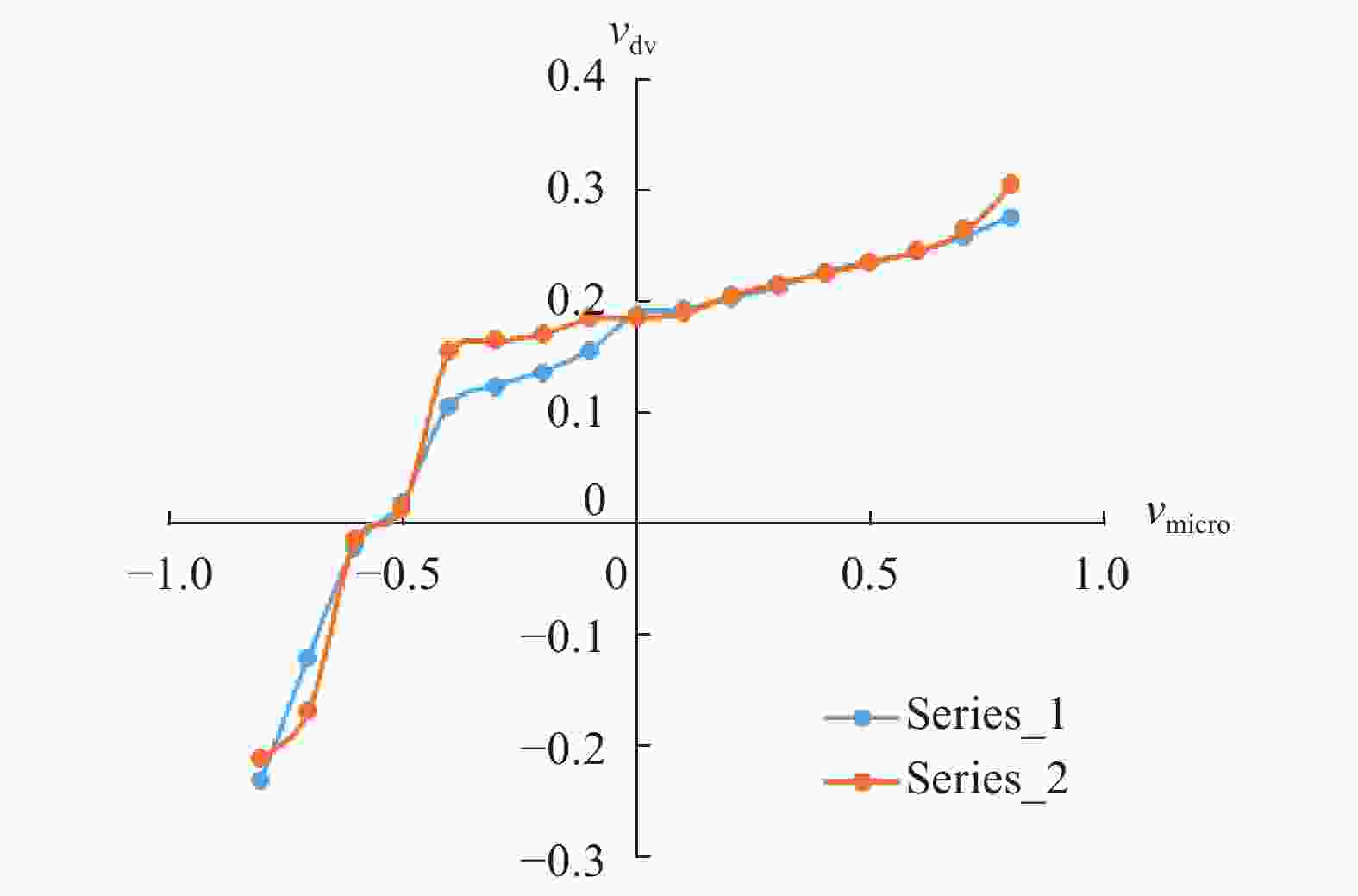
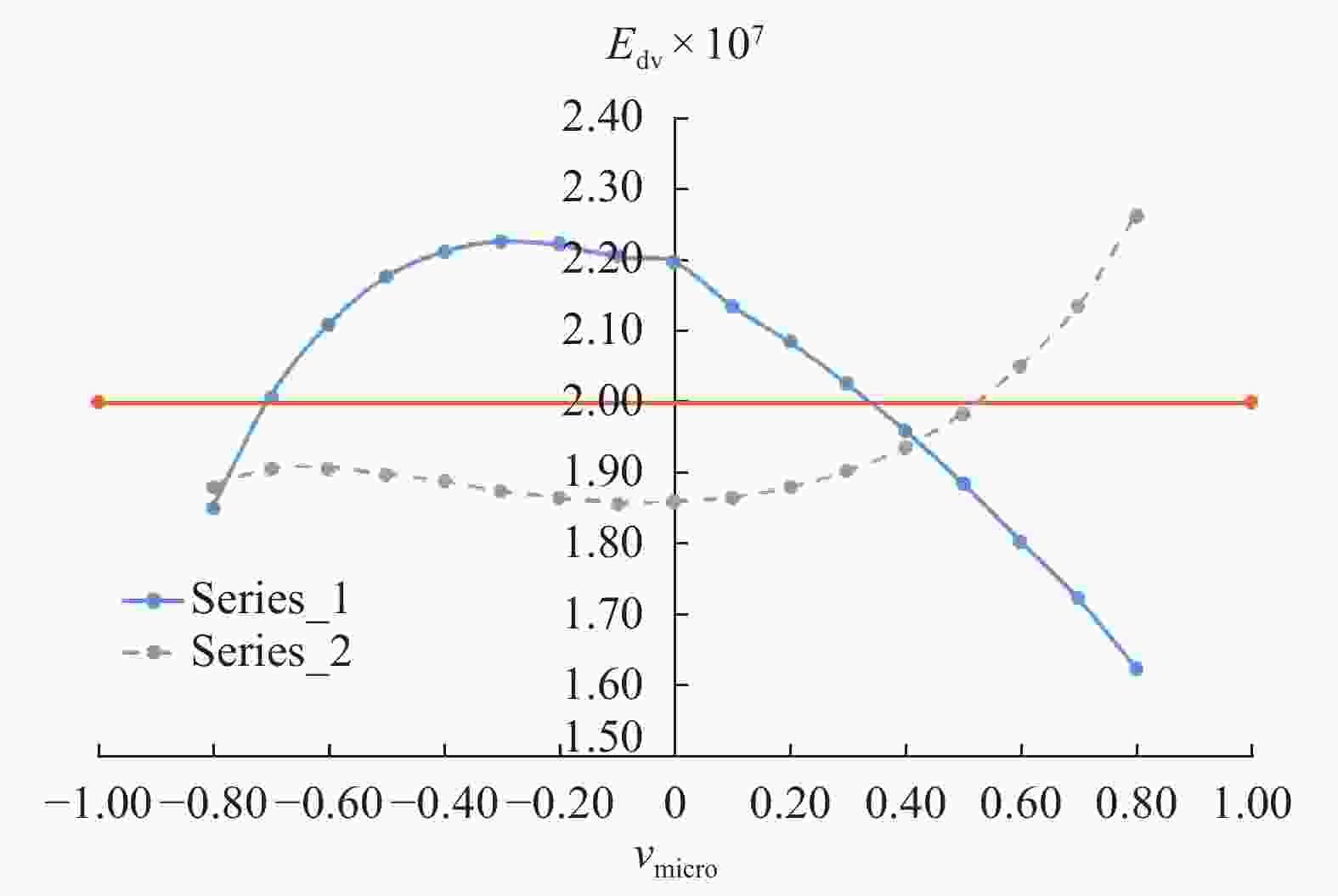
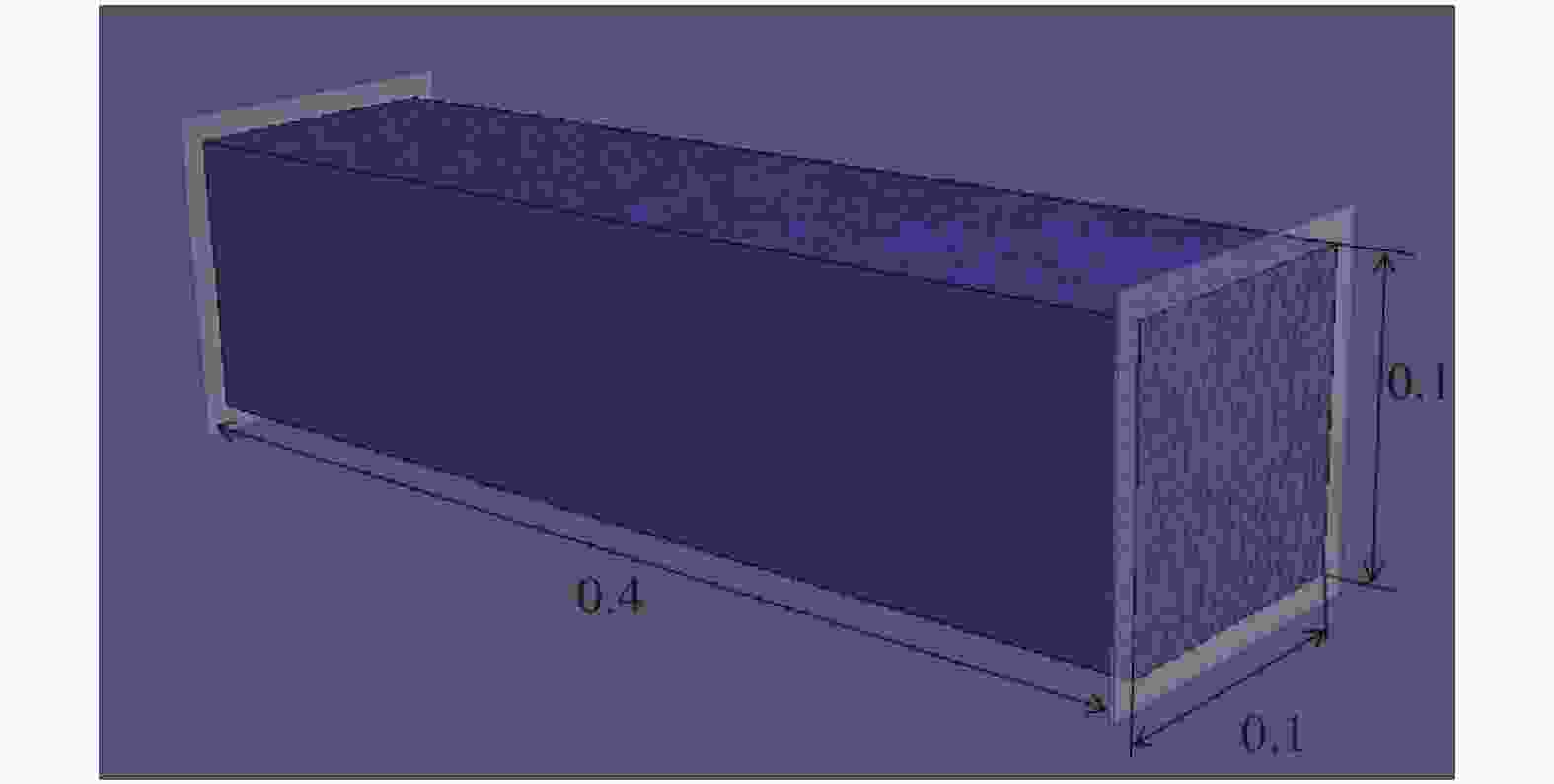
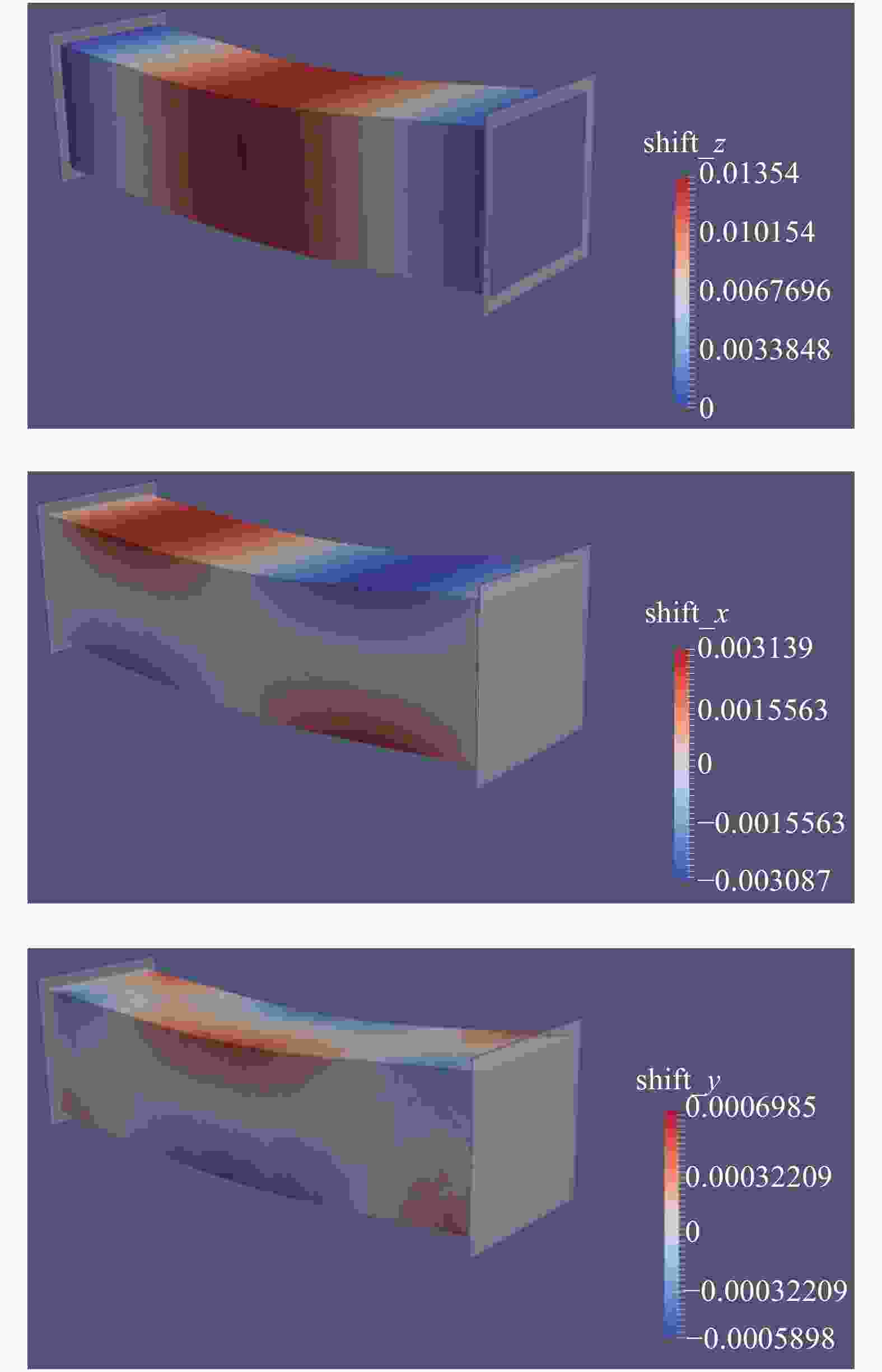
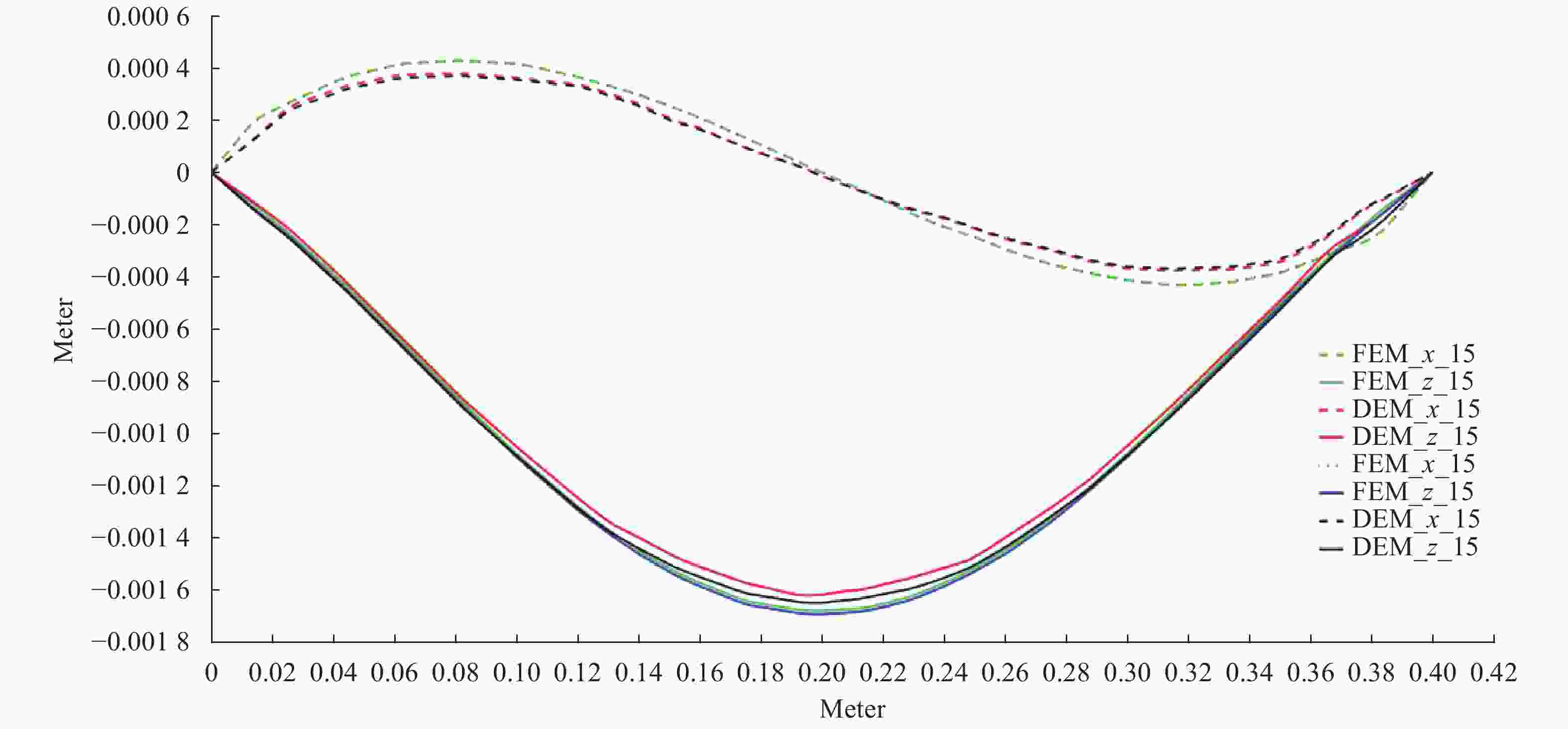
In last time, the series of virtual internal bond model was proposed for solving rock mechanics problems. In these models, the rock continuum is considered as a structure of discrete particles connected by normal and shear springs (bonds). It is well announced that the normal springs structure corresponds to a linear elastic solid with a fixed Poisson ratio, namely, 0.25 for three-dimensional cases. So the shear springs used to represent the diversity of the Poisson ratio. However, the shearing force calculation is not rotationally invariant and it produce difficulties in application of these models for rock mechanics problems with sufficient displacements. In this letter, we proposed the approach to support the diversity of the Poisson ratio that based on usage of deformable Voronoi cells as set of particles. The edges of dual Delaunay tetrahedralization are considered as structure of normal springs (bonds). The movements of particle's centers lead to deformation of tetrahedrals and as result to deformation of Voronoi cells. For each bond, there are the corresponded dual face of some Voronoi cell. We can consider the normal bond as some beam and in this case, the appropriate face of Voronoi cell will be a cross section of this beam. If during deformation the Voronoi face was expand, then, according Poisson effect, the length of bond should be decrees. The above mechanism was numerically investigated and we shown that it is acceptable for simulation of elastic behavior in 0.1–0.3 interval of Poisson ratio. Unexpected surprise is that proposed approach give possibility to simulate auxetic materials with negative Poisson's ratio in interval from –0.5 to –0.1.
In last time, the series of virtual internal bond model was proposed for solving rock mechanics problems. In these models, the rock continuum is considered as a structure of discrete particles connected by normal and shear springs (bonds). It is well announced that the normal springs structure corresponds to a linear elastic solid with a fixed Poisson ratio, namely, 0.25 for three-dimensional cases. So the shear springs used to represent the diversity of the Poisson ratio. However, the shearing force calculation is not rotationally invariant and it produce difficulties in application of these models for rock mechanics problems with sufficient displacements. In this letter, we proposed the approach to support the diversity of the Poisson ratio that based on usage of deformable Voronoi cells as set of particles. The edges of dual Delaunay tetrahedralization are considered as structure of normal springs (bonds). The movements of particle's centers lead to deformation of tetrahedrals and as result to deformation of Voronoi cells. For each bond, there are the corresponded dual face of some Voronoi cell. We can consider the normal bond as some beam and in this case, the appropriate face of Voronoi cell will be a cross section of this beam. If during deformation the Voronoi face was expand, then, according Poisson effect, the length of bond should be decrees. The above mechanism was numerically investigated and we shown that it is acceptable for simulation of elastic behavior in 0.1–0.3 interval of Poisson ratio. Unexpected surprise is that proposed approach give possibility to simulate auxetic materials with negative Poisson's ratio in interval from –0.5 to –0.1.
Theoretical and Applied Mechanics Letters 2020, 10(2): 92-97.
doi: 10.1016/j.taml.2020.01.012
Abstract:
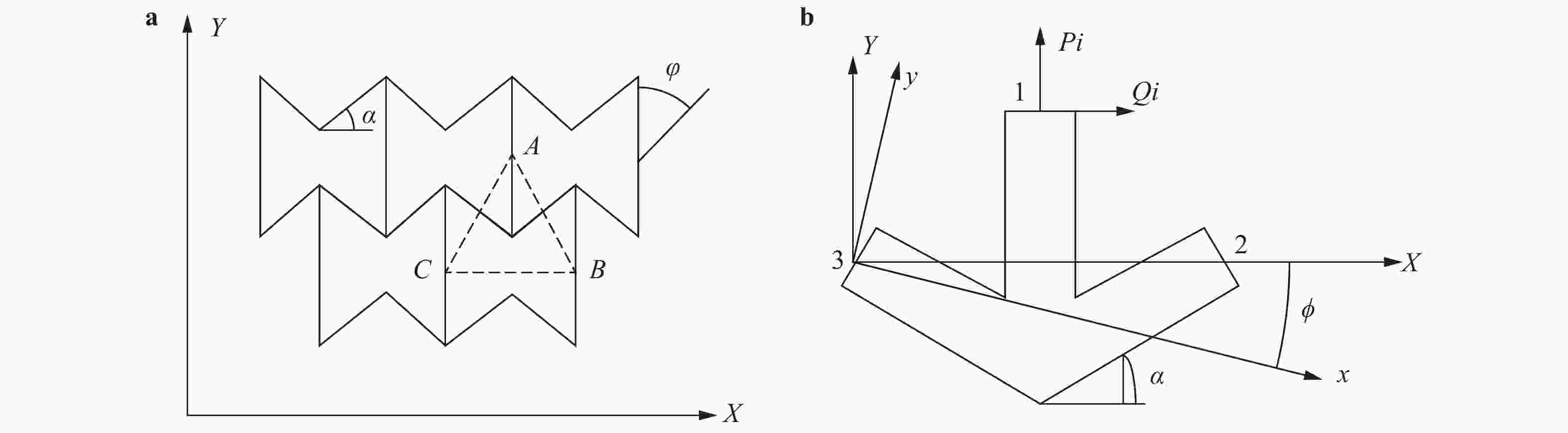
The construction of mechanical-mathematical model and numerical method for the deformation processes of rock massifs with goafs and underground structures is very complex and also important task in modern rock mechanics. In this study, the mechanical-mathematical model is developed for rock massif in vicinity of underground goafs considering the internal block-layered structure of the rock massif. A new constitutive model is introduced in this study to describe the negative Poisson's ratio for the lock-layered structure. Two types of defining equations systems for studying the state of a rock massif taking into account the block-layered structure are described. Finally, several examples are given using the present mechanical-mathematical model.
The construction of mechanical-mathematical model and numerical method for the deformation processes of rock massifs with goafs and underground structures is very complex and also important task in modern rock mechanics. In this study, the mechanical-mathematical model is developed for rock massif in vicinity of underground goafs considering the internal block-layered structure of the rock massif. A new constitutive model is introduced in this study to describe the negative Poisson's ratio for the lock-layered structure. Two types of defining equations systems for studying the state of a rock massif taking into account the block-layered structure are described. Finally, several examples are given using the present mechanical-mathematical model.
Theoretical and Applied Mechanics Letters 2020, 10(2): 116-119.
doi: 10.1016/j.taml.2020.01.015
Abstract:
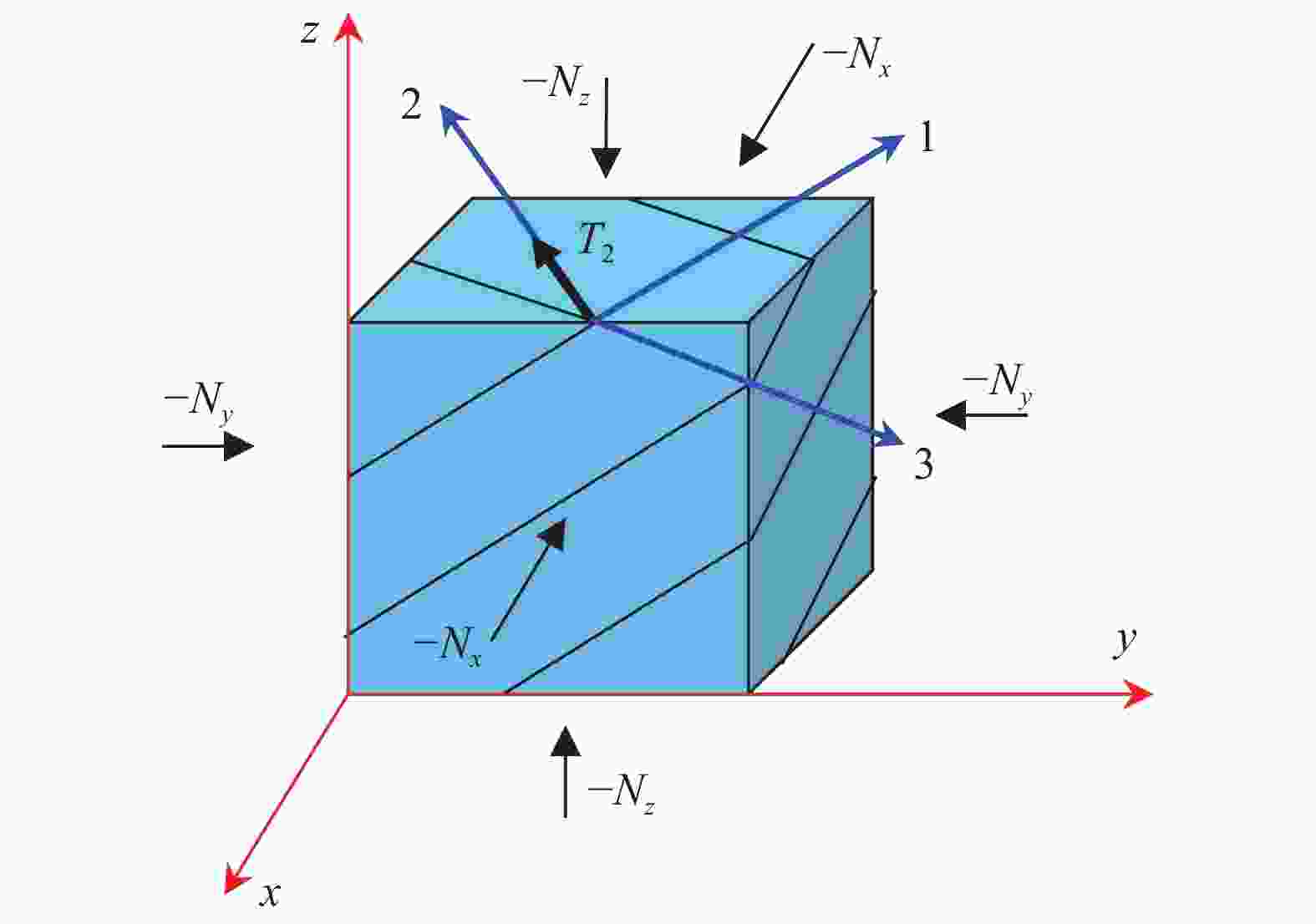
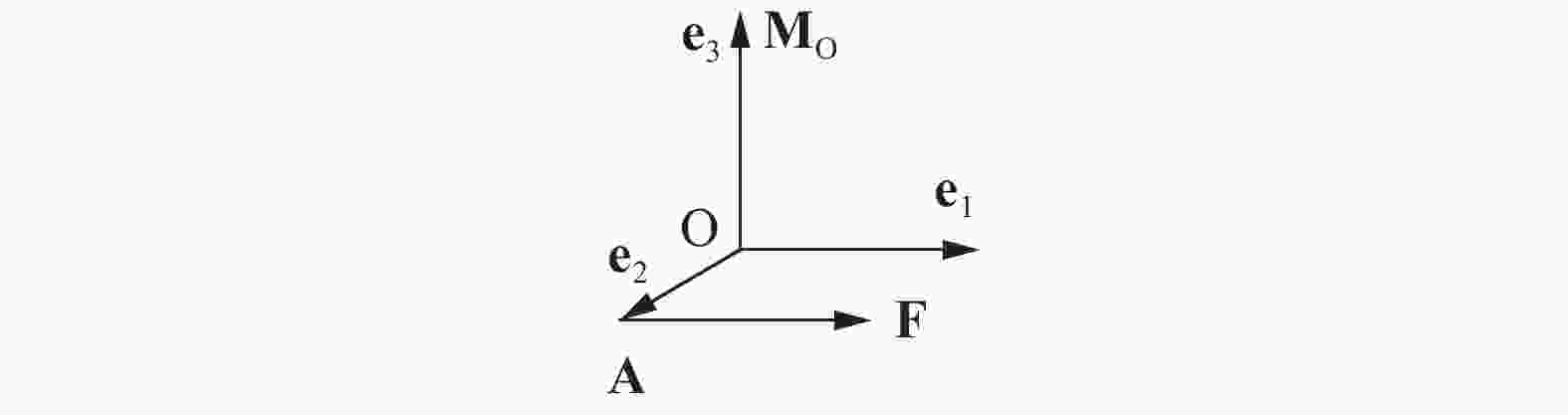
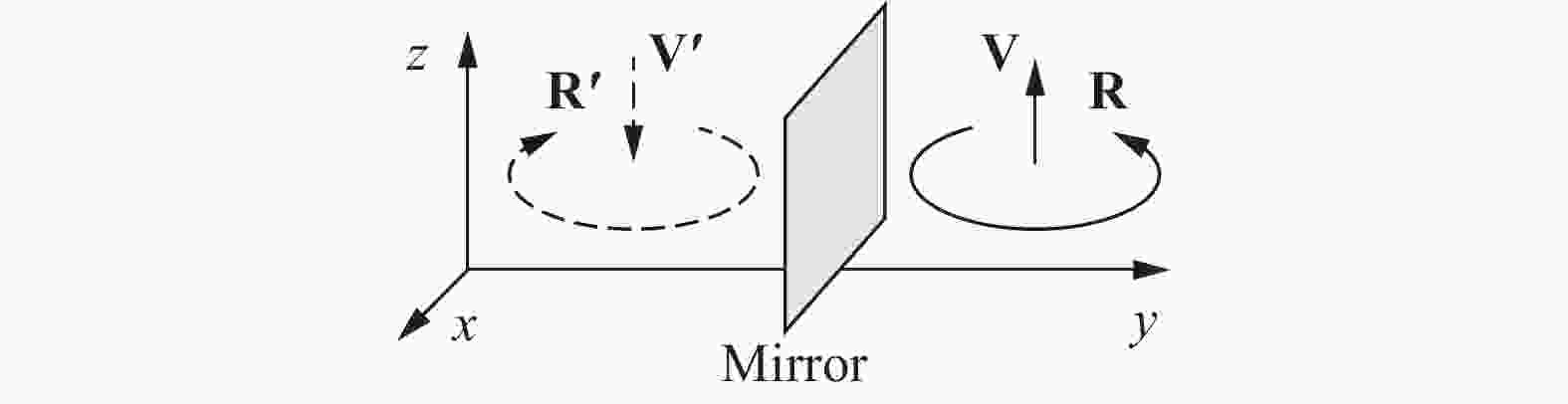
Under improper transformations, the traditional transformation laws for cross products, the permutation tensor, and rotations are incorrect. For a cross product, using a counter-example the left-hand rule is proved wrong. The unique rule for a cross product is the right-hand rule. Coordinate systems have handedness, while a cross product is frame-indifference. Since the permutation tensor is defined as a triple product including a cross product, the law for the permutation tensor is false. For a rotation, its pseudovector representation is incorrect, because the mirror is an auxiliary device to produce the virtual image rather than a new coordinate system or reference frame.
Under improper transformations, the traditional transformation laws for cross products, the permutation tensor, and rotations are incorrect. For a cross product, using a counter-example the left-hand rule is proved wrong. The unique rule for a cross product is the right-hand rule. Coordinate systems have handedness, while a cross product is frame-indifference. Since the permutation tensor is defined as a triple product including a cross product, the law for the permutation tensor is false. For a rotation, its pseudovector representation is incorrect, because the mirror is an auxiliary device to produce the virtual image rather than a new coordinate system or reference frame.
Theoretical and Applied Mechanics Letters 2020, 10(2): 120-124.
doi: 10.1016/j.taml.2020.01.018
Abstract:
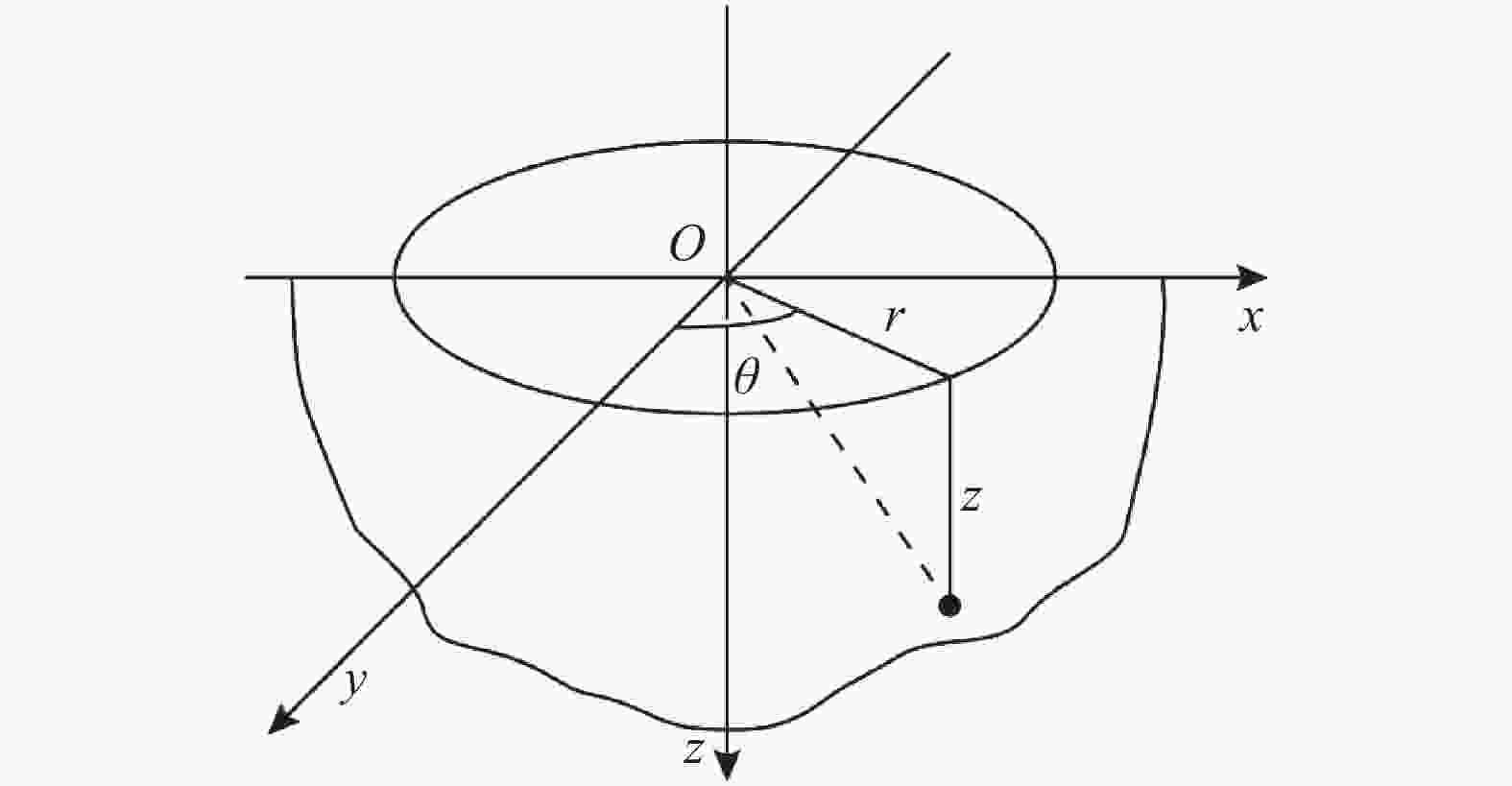
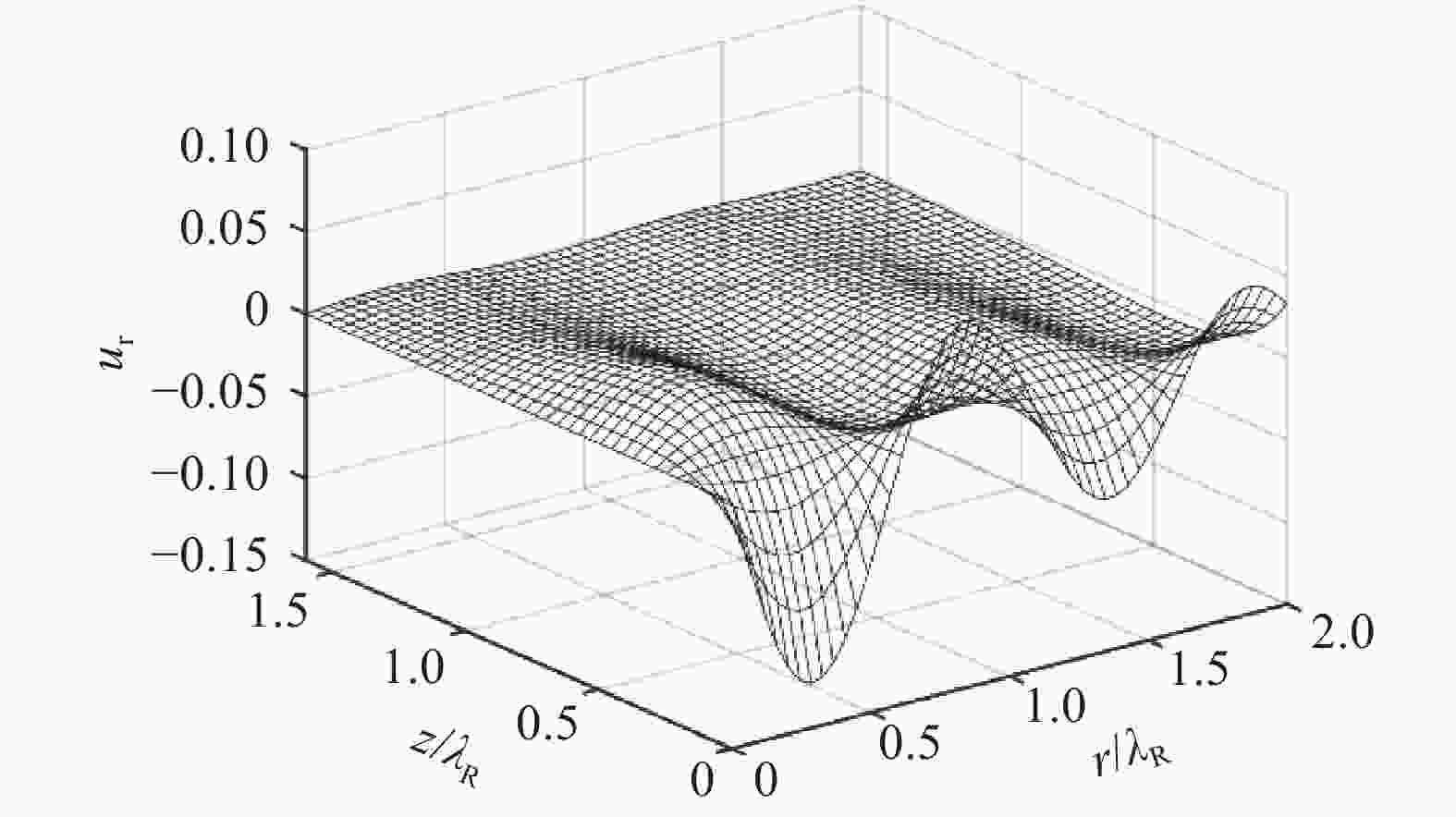
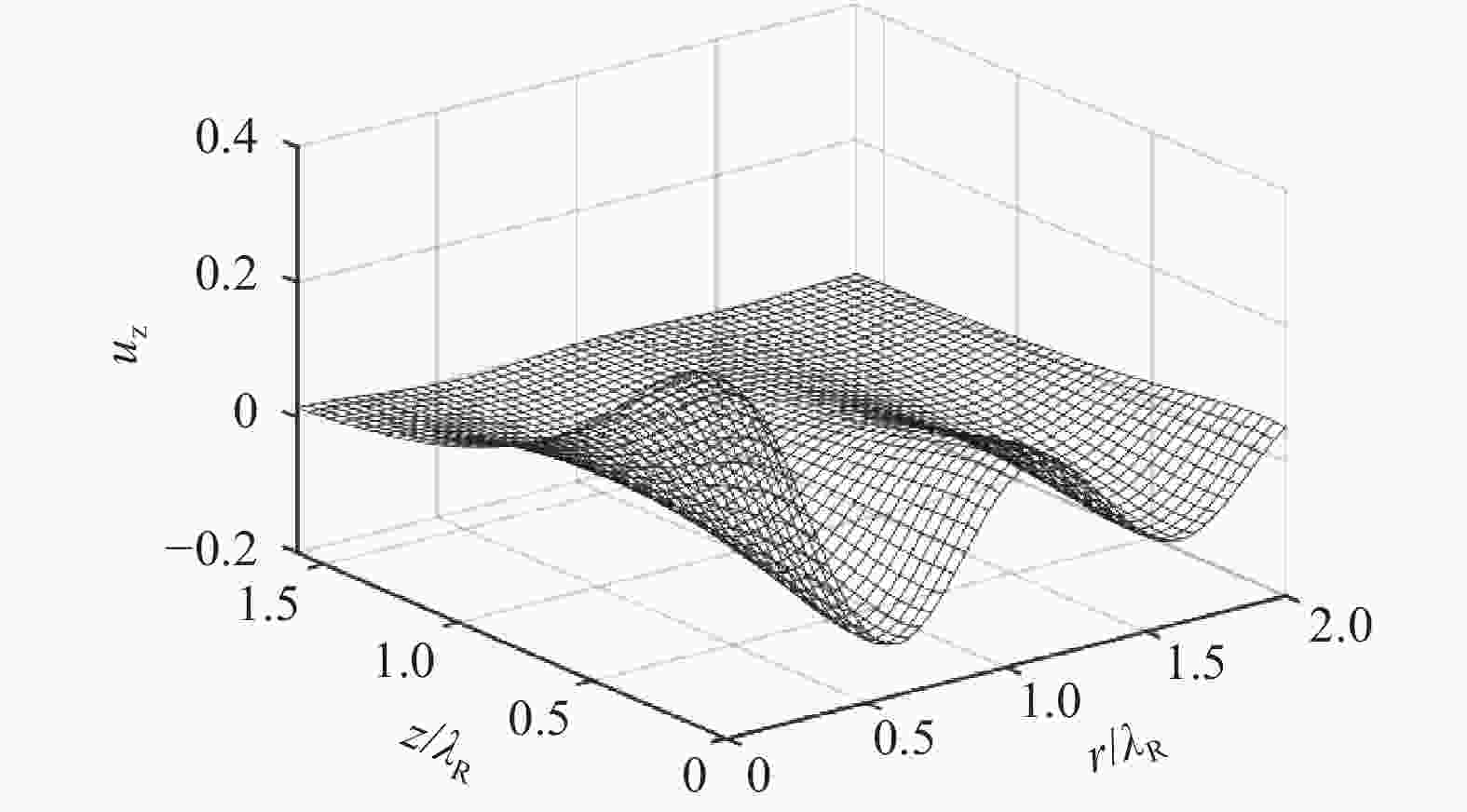
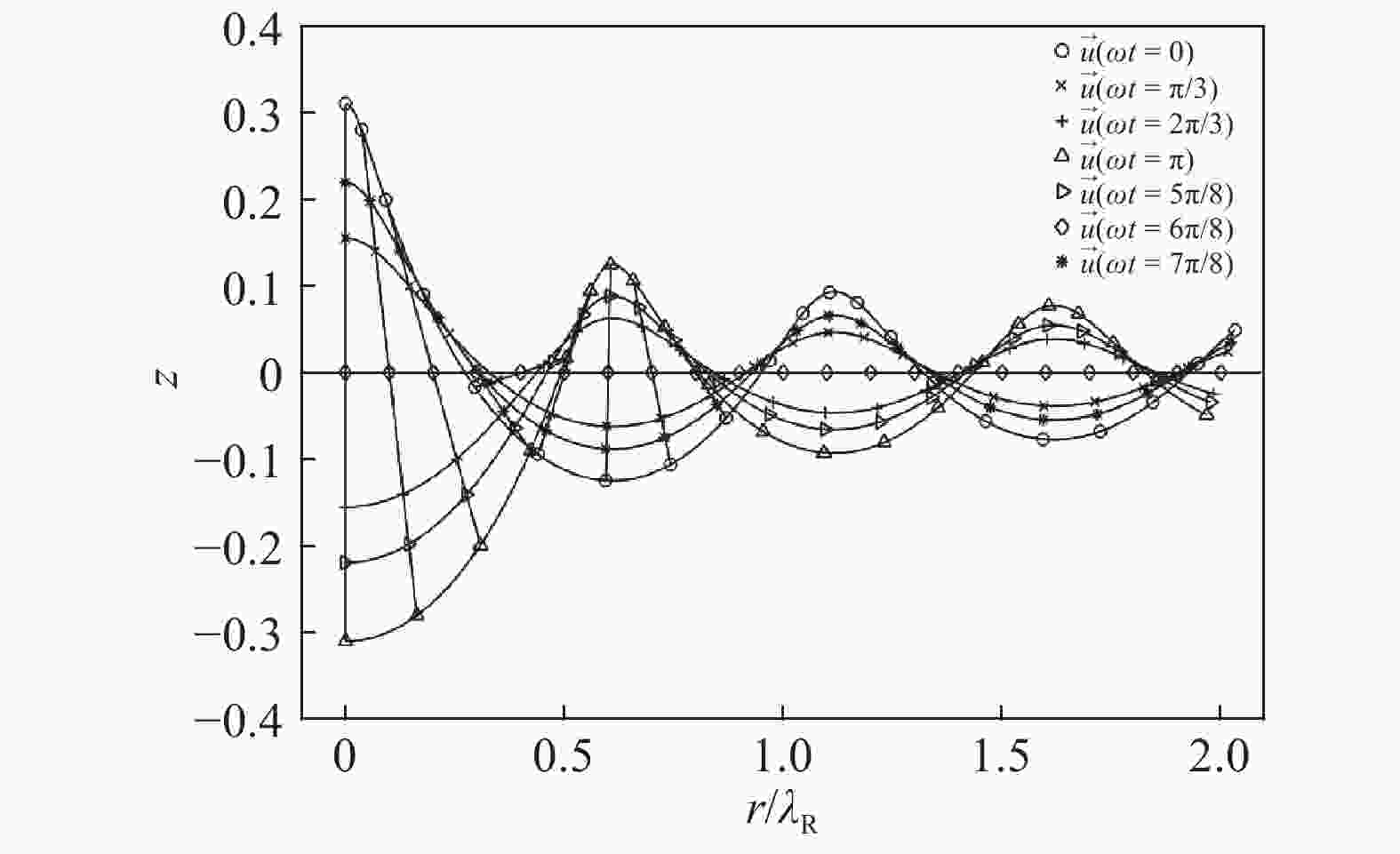
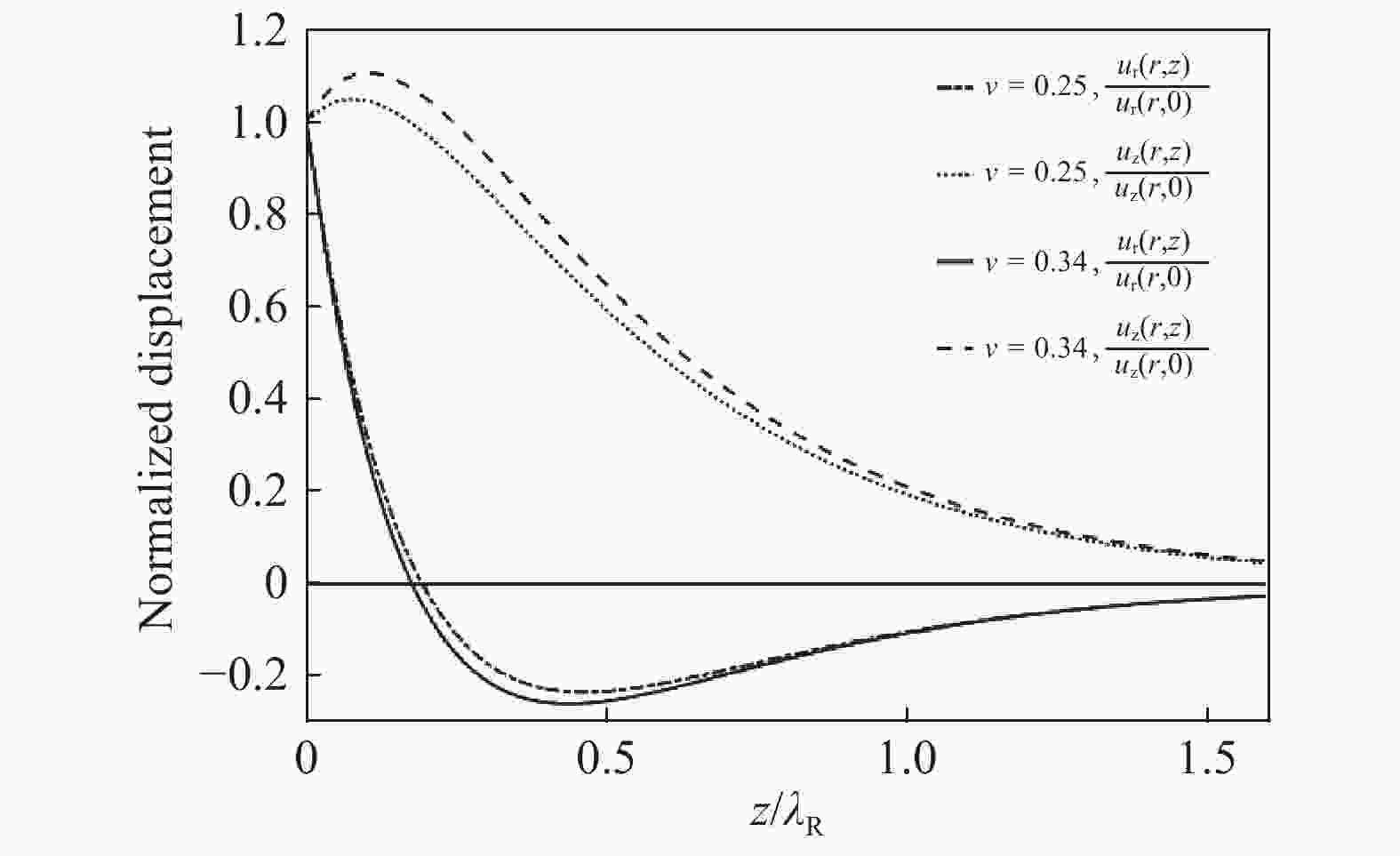
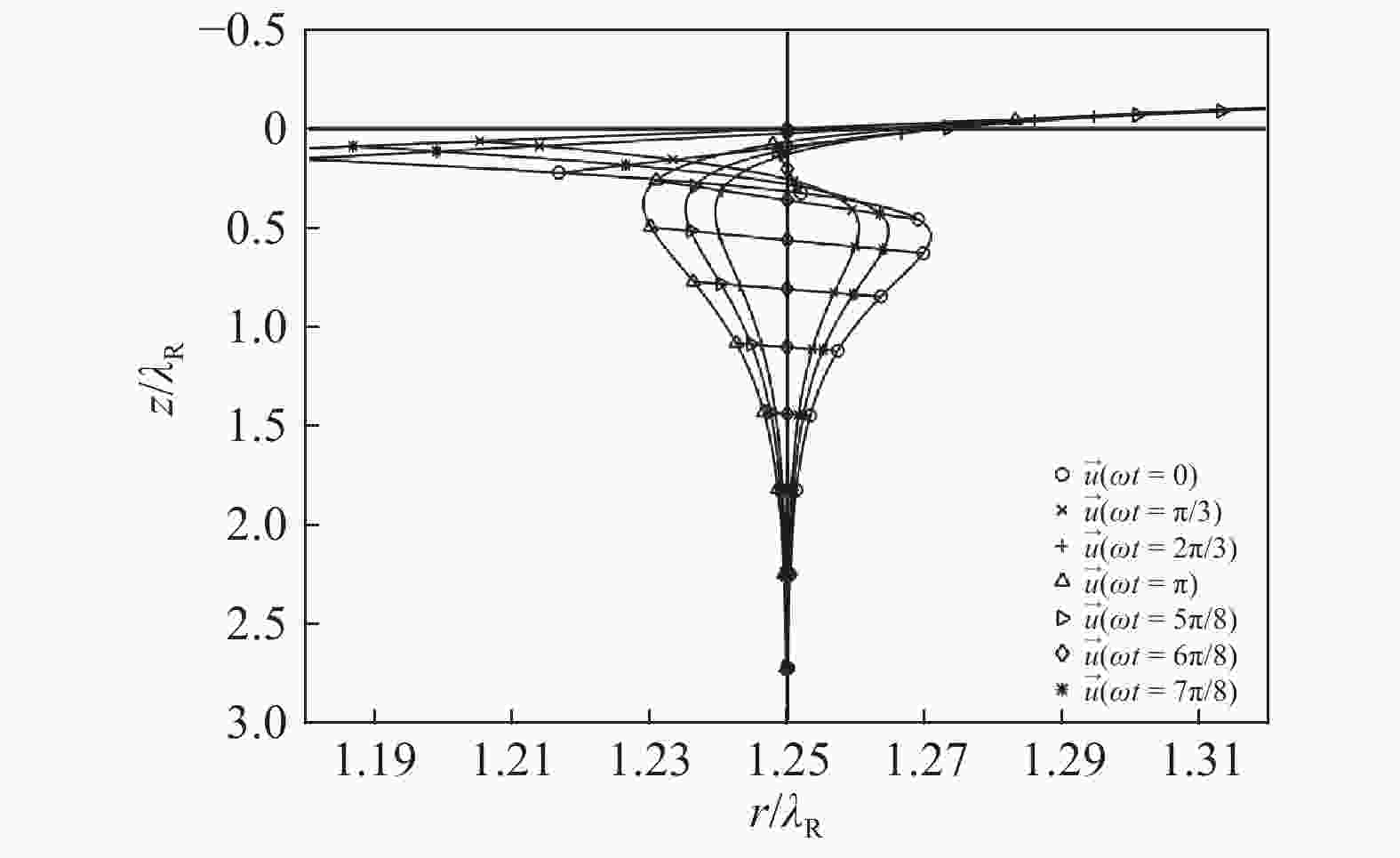
It is well-known that Rayleigh wave, also known as surface acoustic wave (SAW), solutions in semi-infinite solids are plane waves with signatory properties like the distinct velocity and exponentially decaying deformation in the depth. Applications of Rayleigh waves are focused on the deformation and energy in the vicinity of surface of solids and less loss in the propagation. A generalized model of Rayleigh waves in axisymmetric mode is established and solutions are obtained with cylindrical coordinates. It is found that the Rayleigh waves also propagate in the axisymmetric mode with slow decay in radius, confirming the existence of surface acoustic waves is irrelevant to coordinate system. On the other hand, the solutions can be treated as plane waves in regions far away from the source. Furthermore, the particle trajectory of axisymmetric SAW is a line with constant slope rather than the signatory ellipse in Cartesian coordinate case.
It is well-known that Rayleigh wave, also known as surface acoustic wave (SAW), solutions in semi-infinite solids are plane waves with signatory properties like the distinct velocity and exponentially decaying deformation in the depth. Applications of Rayleigh waves are focused on the deformation and energy in the vicinity of surface of solids and less loss in the propagation. A generalized model of Rayleigh waves in axisymmetric mode is established and solutions are obtained with cylindrical coordinates. It is found that the Rayleigh waves also propagate in the axisymmetric mode with slow decay in radius, confirming the existence of surface acoustic waves is irrelevant to coordinate system. On the other hand, the solutions can be treated as plane waves in regions far away from the source. Furthermore, the particle trajectory of axisymmetric SAW is a line with constant slope rather than the signatory ellipse in Cartesian coordinate case.
Theoretical and Applied Mechanics Letters 2020, 10(2): 125-131.
doi: 10.1016/j.taml.2020.01.011
Abstract:
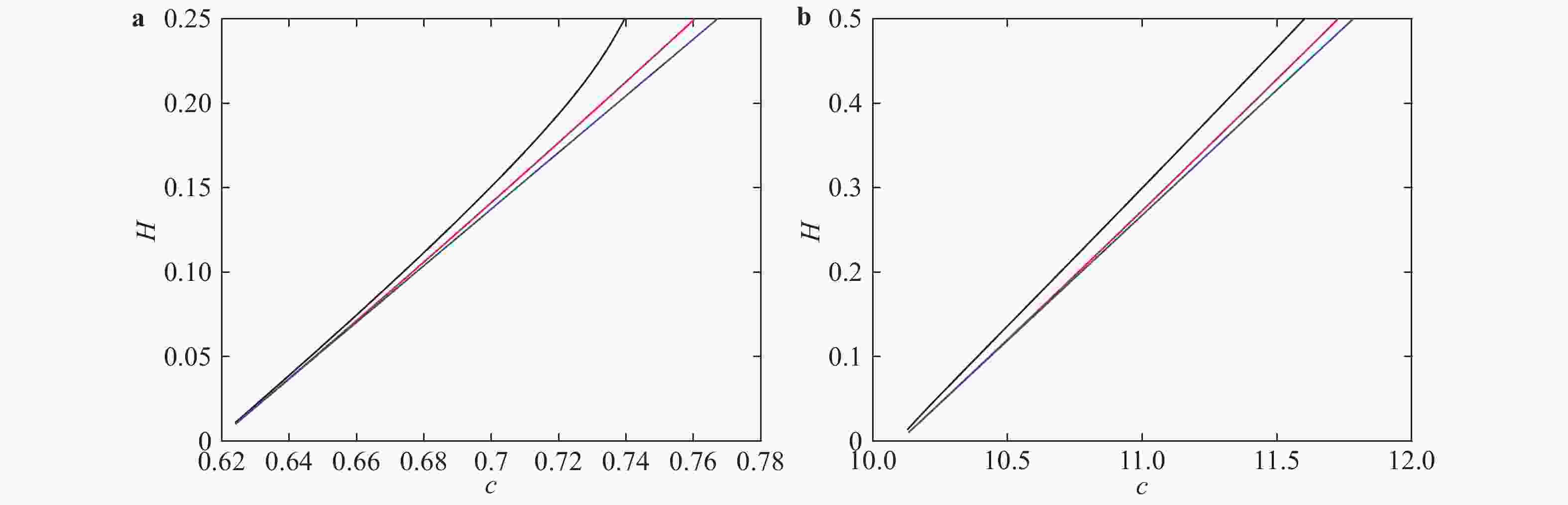
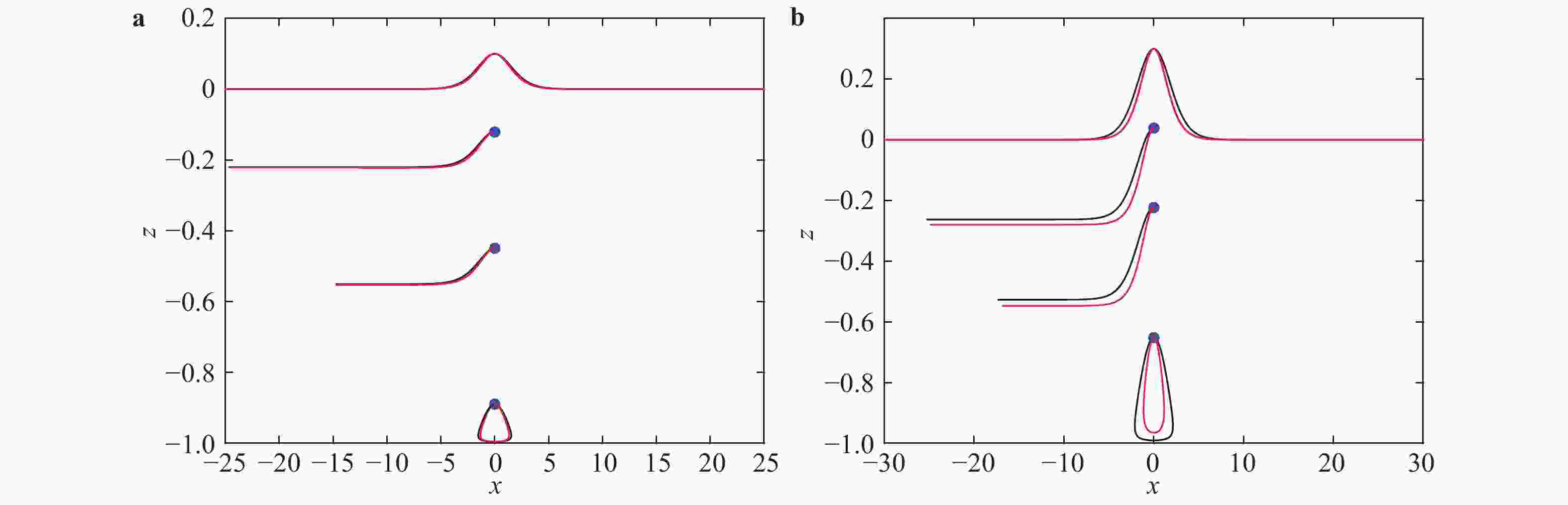
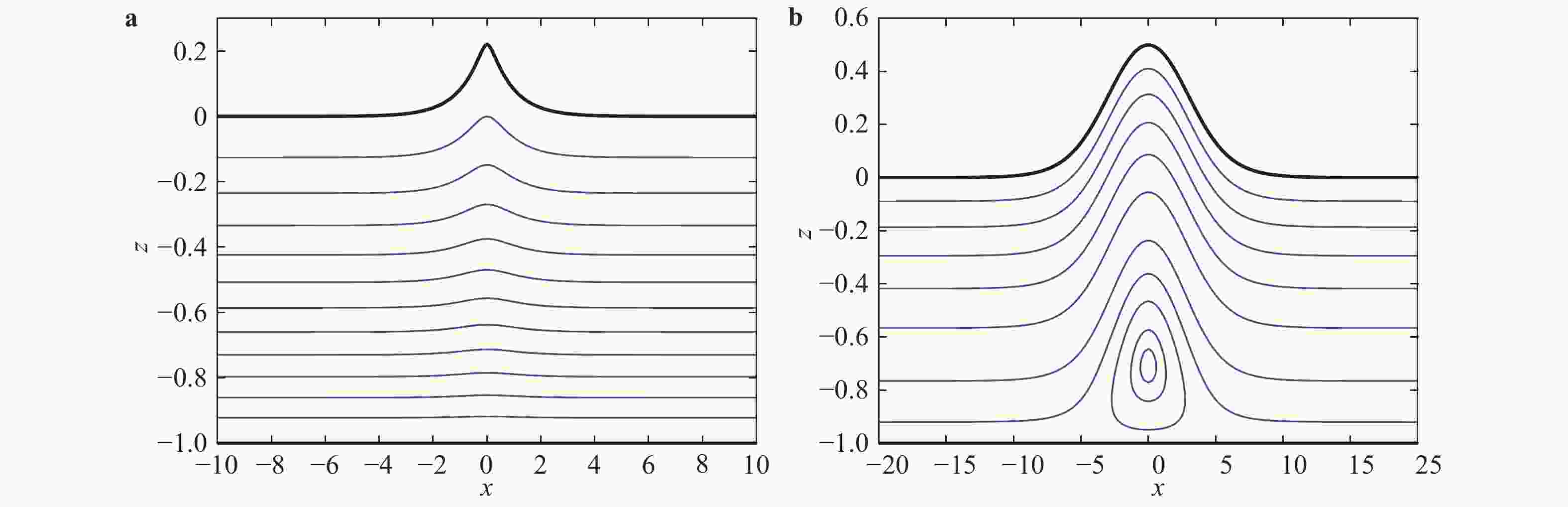
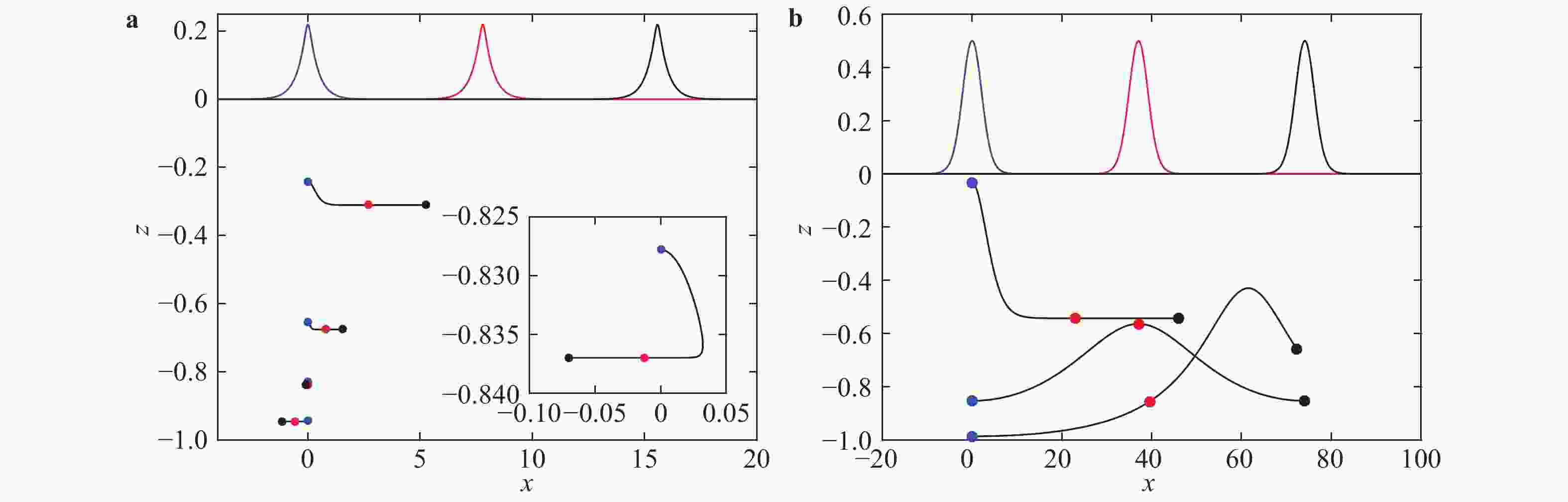
This paper is concerned with particle trajectories beneath solitary waves when a linear shear current exists. The fluid is assumed to be incompressible and inviscid, lying on a flat bed. Classical asymptotic expansion is used to obtain a Korteweg-de Vries (KdV) equation, then a forth-order Runge-Kutta method is applied to get the approximate particle trajectories. On the other hand, our particular attention is paid to the direct numerical simulation (DNS) to the original Euler equations. A conformal map is used to solve the nonlinear boundary value problem. High-accuracy numerical solutions are then obtained through the fast Fourier transform (FFT) and compared with the asymptotic solutions, which shows a good agreement when wave amplitude is small. Further, it also yields that there are different types of particle trajectories. Most surprisingly, periodic motion of particles could exist under solitary waves, which is due to the wave-current interaction.
This paper is concerned with particle trajectories beneath solitary waves when a linear shear current exists. The fluid is assumed to be incompressible and inviscid, lying on a flat bed. Classical asymptotic expansion is used to obtain a Korteweg-de Vries (KdV) equation, then a forth-order Runge-Kutta method is applied to get the approximate particle trajectories. On the other hand, our particular attention is paid to the direct numerical simulation (DNS) to the original Euler equations. A conformal map is used to solve the nonlinear boundary value problem. High-accuracy numerical solutions are then obtained through the fast Fourier transform (FFT) and compared with the asymptotic solutions, which shows a good agreement when wave amplitude is small. Further, it also yields that there are different types of particle trajectories. Most surprisingly, periodic motion of particles could exist under solitary waves, which is due to the wave-current interaction.
Theoretical and Applied Mechanics Letters 2020, 10(2): 132-140.
doi: 10.1016/j.taml.2020.01.016
Abstract:
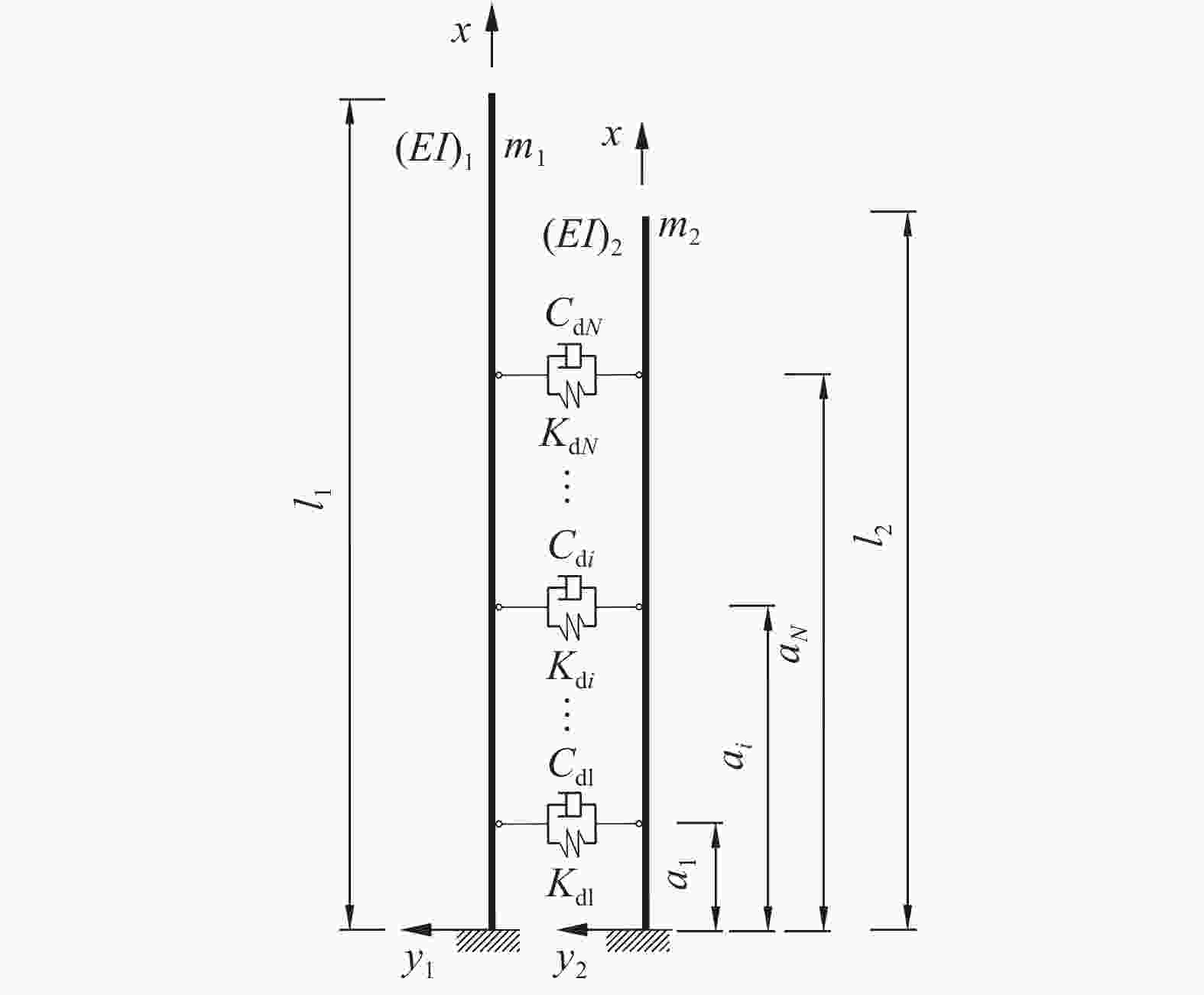
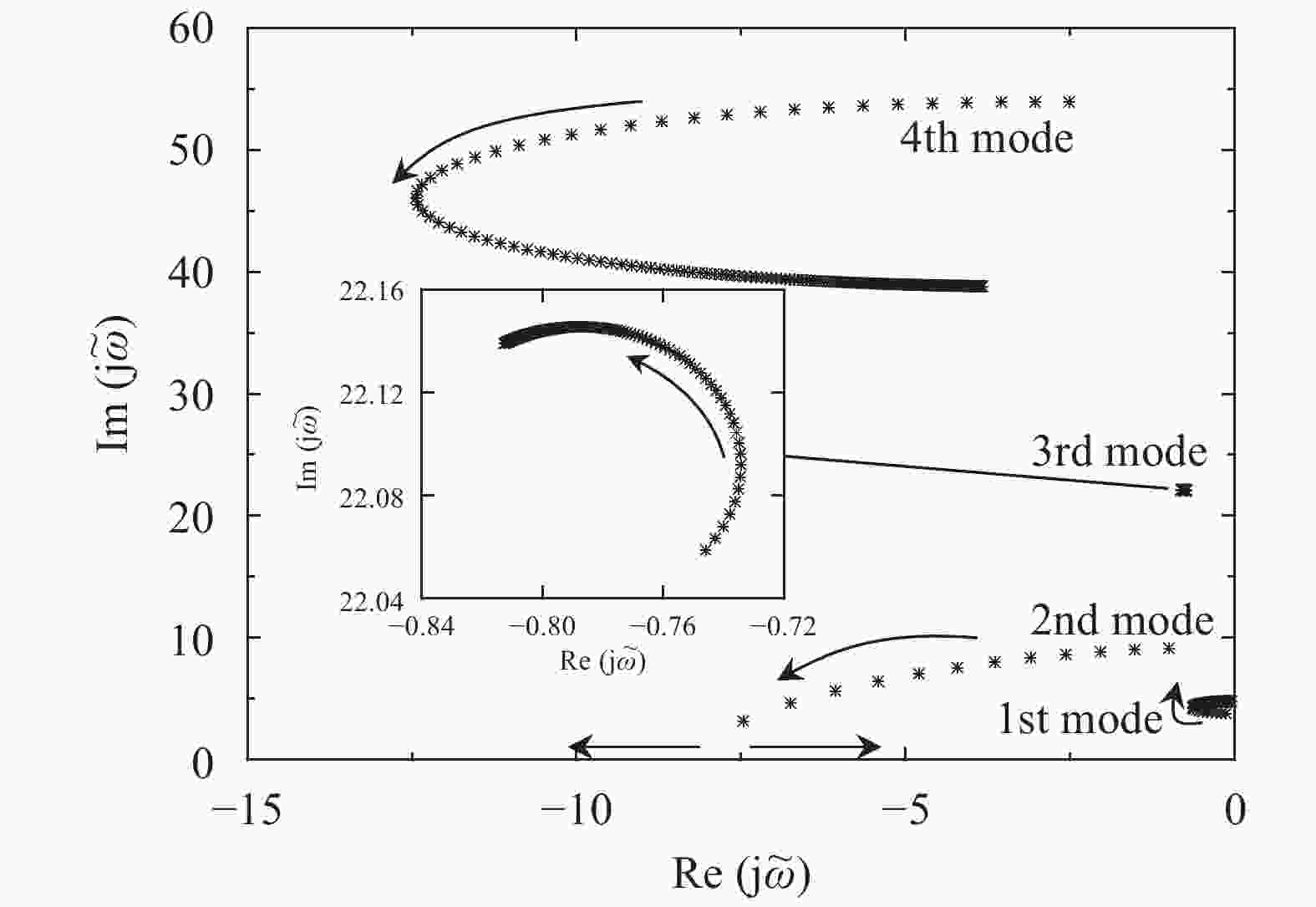
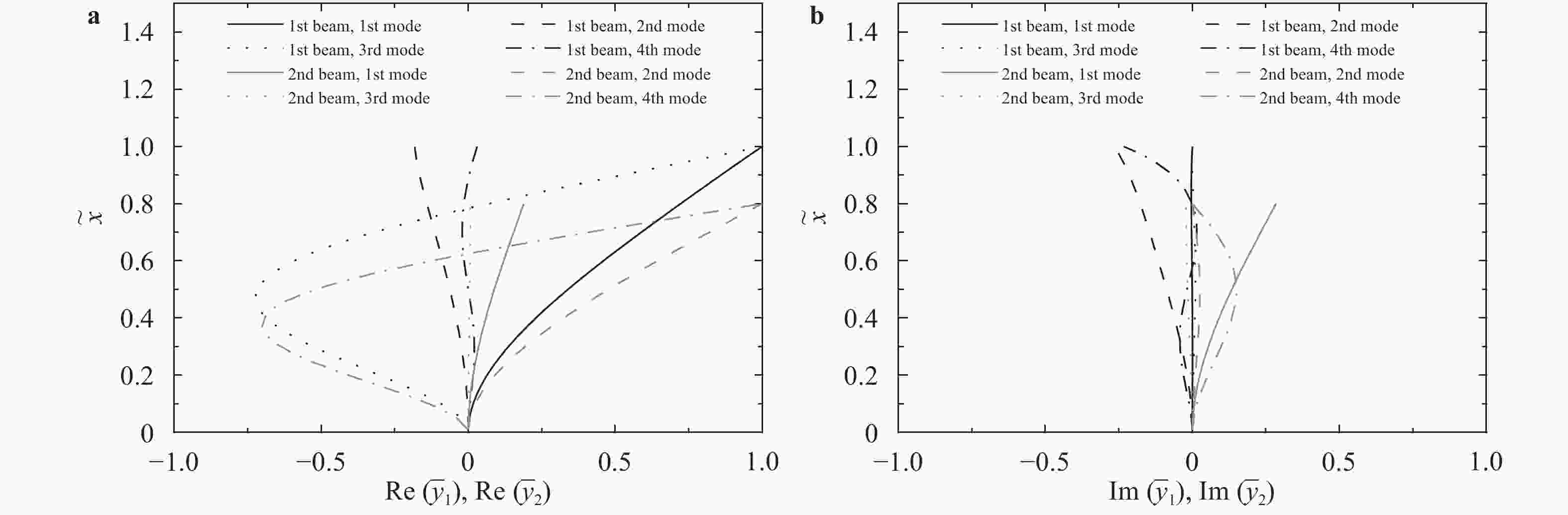
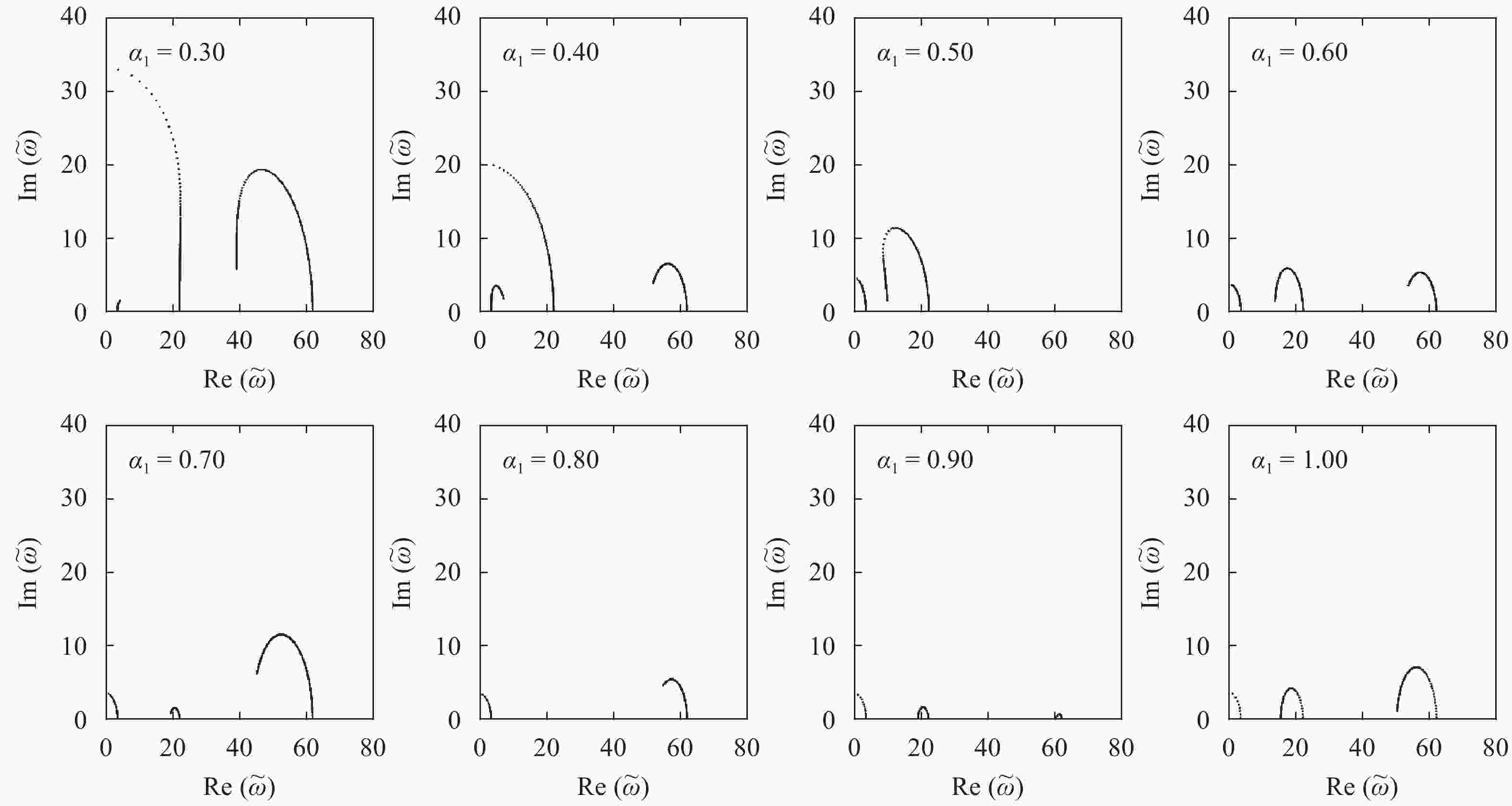
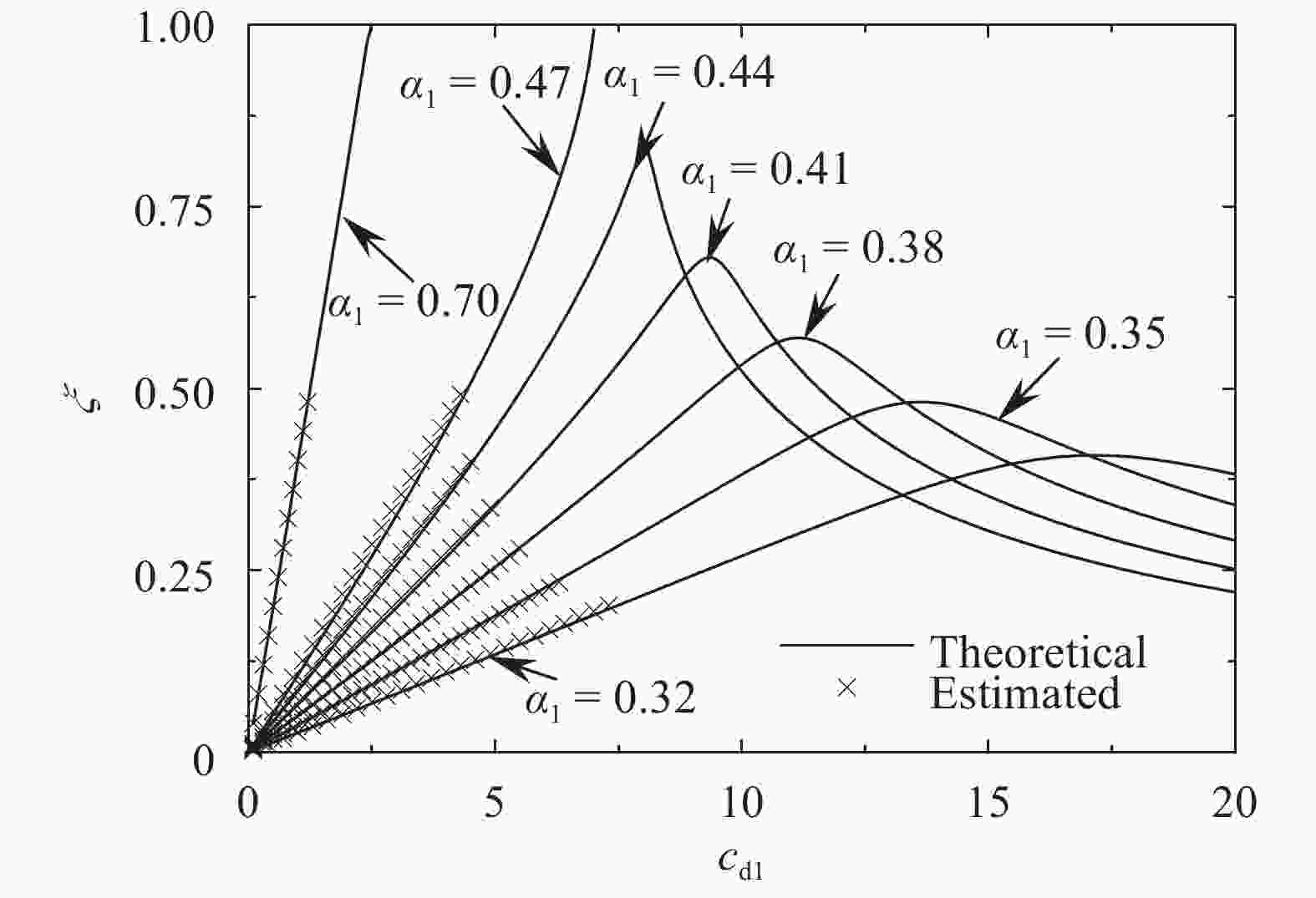
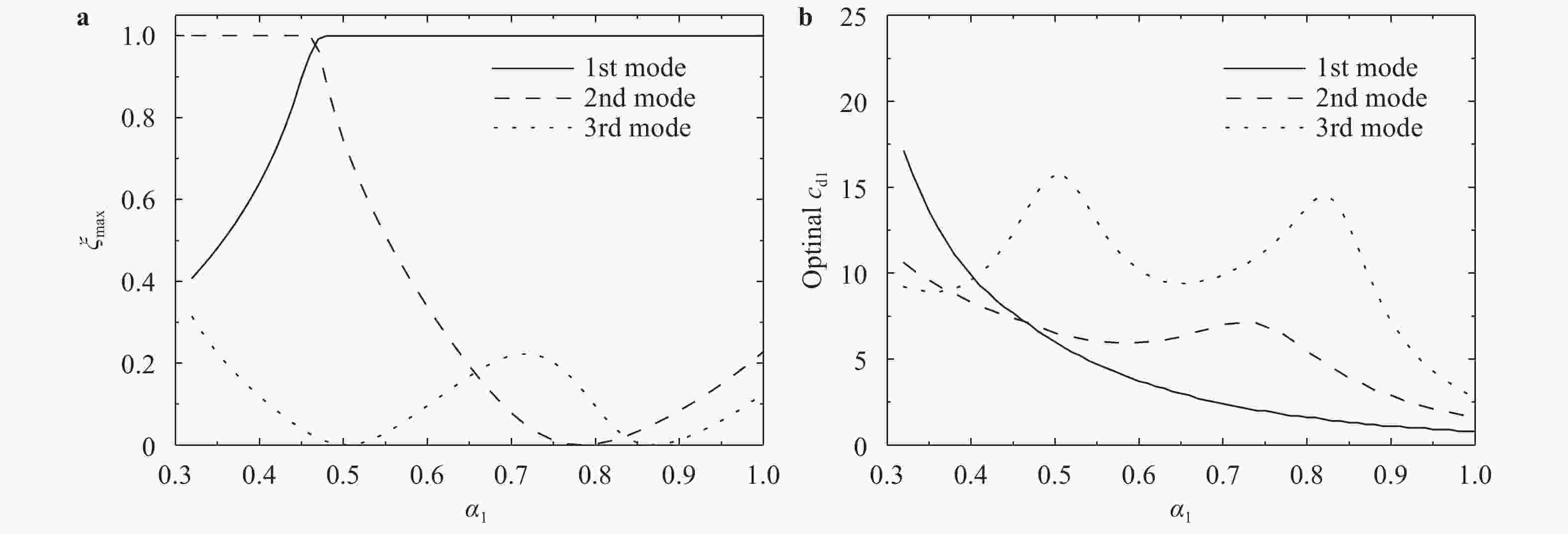
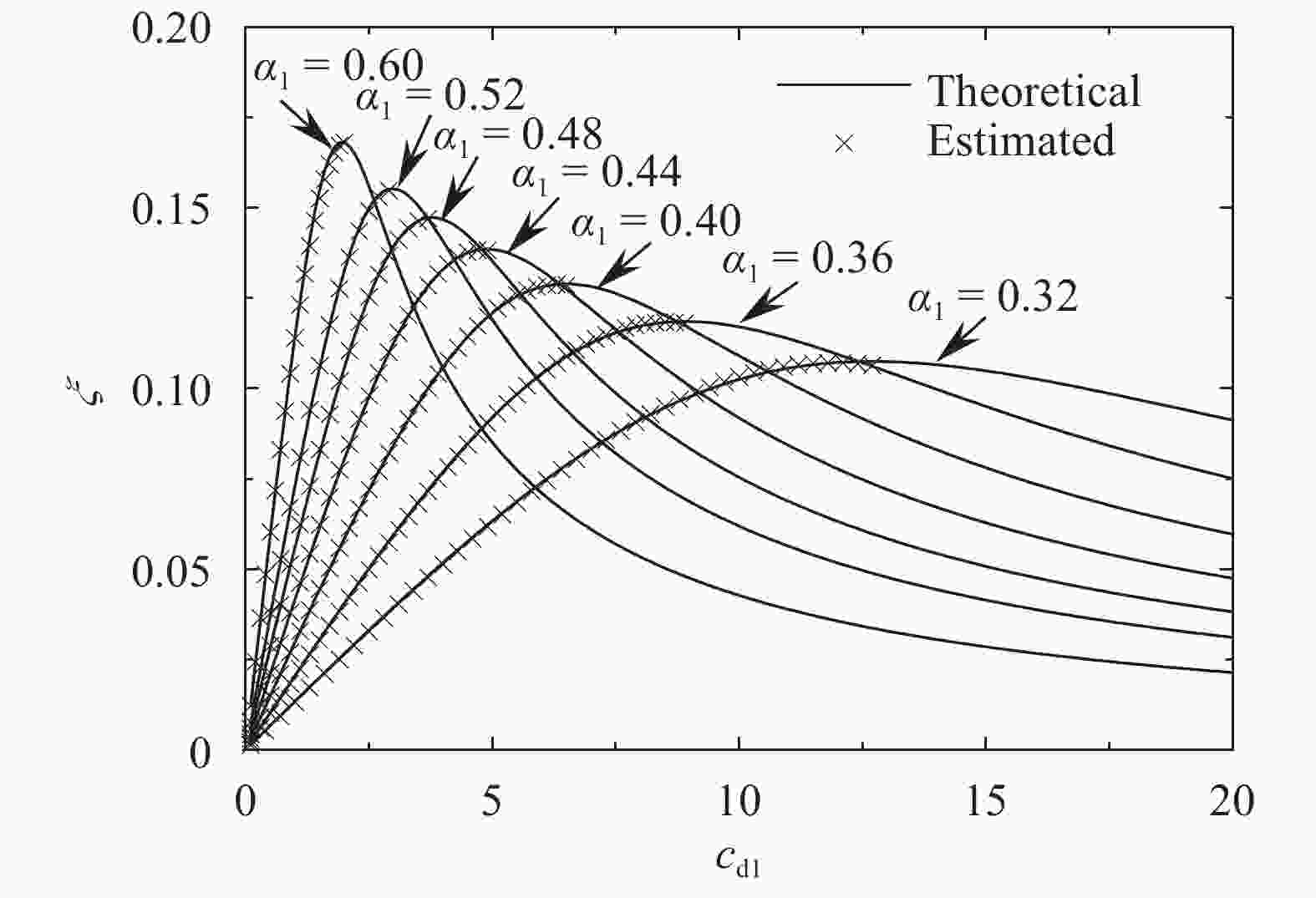
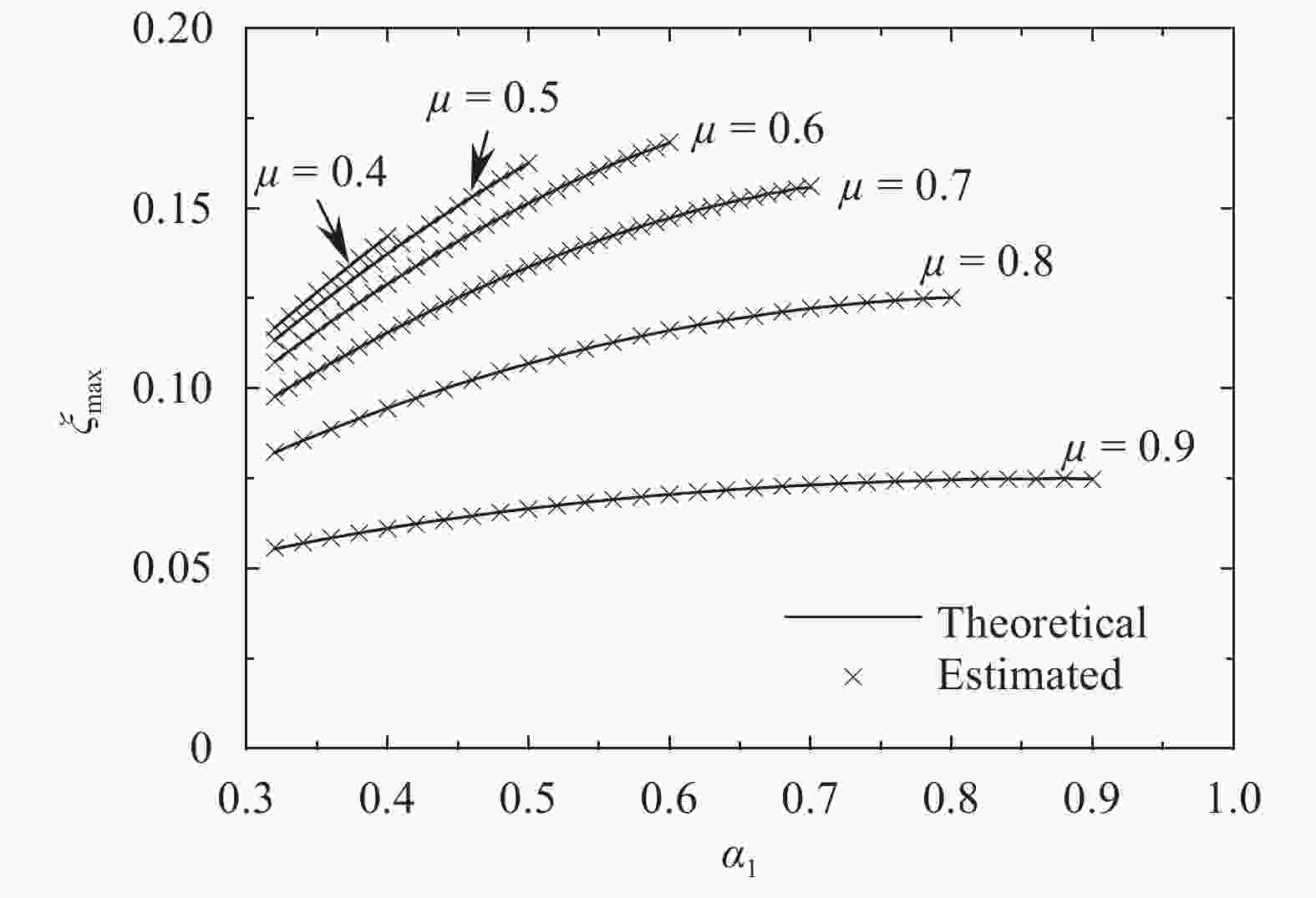
With consideration of a high-rise coupled building system, a flexible beams-based analytical model is setup to characterize the dynamic behavior of the system. The general motion equation for the two beams interconnected by multiple viscous/visco-elastic dampers is rewritten into a non-dimensional form to identify the minimal set of parameters governing the dynamic characteristics. The corresponding exact solution suitable for arbitrary boundary conditions is presented. Furthermore, the methodology for computing the coefficients of the modal shape function is proposed. As an example, the explicit expression of the modal shape function is derived, provided only one damper is adopted to connect the adjacent buildings. Finally, to validate the proposed methodologies, three case studies are performed, in which the existence of the overdamping and the optimal damping coefficient are revealed. In the case of using one damper in connecting two similar buildings, the estimating equations for the first modal damping ratio are formulated.
With consideration of a high-rise coupled building system, a flexible beams-based analytical model is setup to characterize the dynamic behavior of the system. The general motion equation for the two beams interconnected by multiple viscous/visco-elastic dampers is rewritten into a non-dimensional form to identify the minimal set of parameters governing the dynamic characteristics. The corresponding exact solution suitable for arbitrary boundary conditions is presented. Furthermore, the methodology for computing the coefficients of the modal shape function is proposed. As an example, the explicit expression of the modal shape function is derived, provided only one damper is adopted to connect the adjacent buildings. Finally, to validate the proposed methodologies, three case studies are performed, in which the existence of the overdamping and the optimal damping coefficient are revealed. In the case of using one damper in connecting two similar buildings, the estimating equations for the first modal damping ratio are formulated.
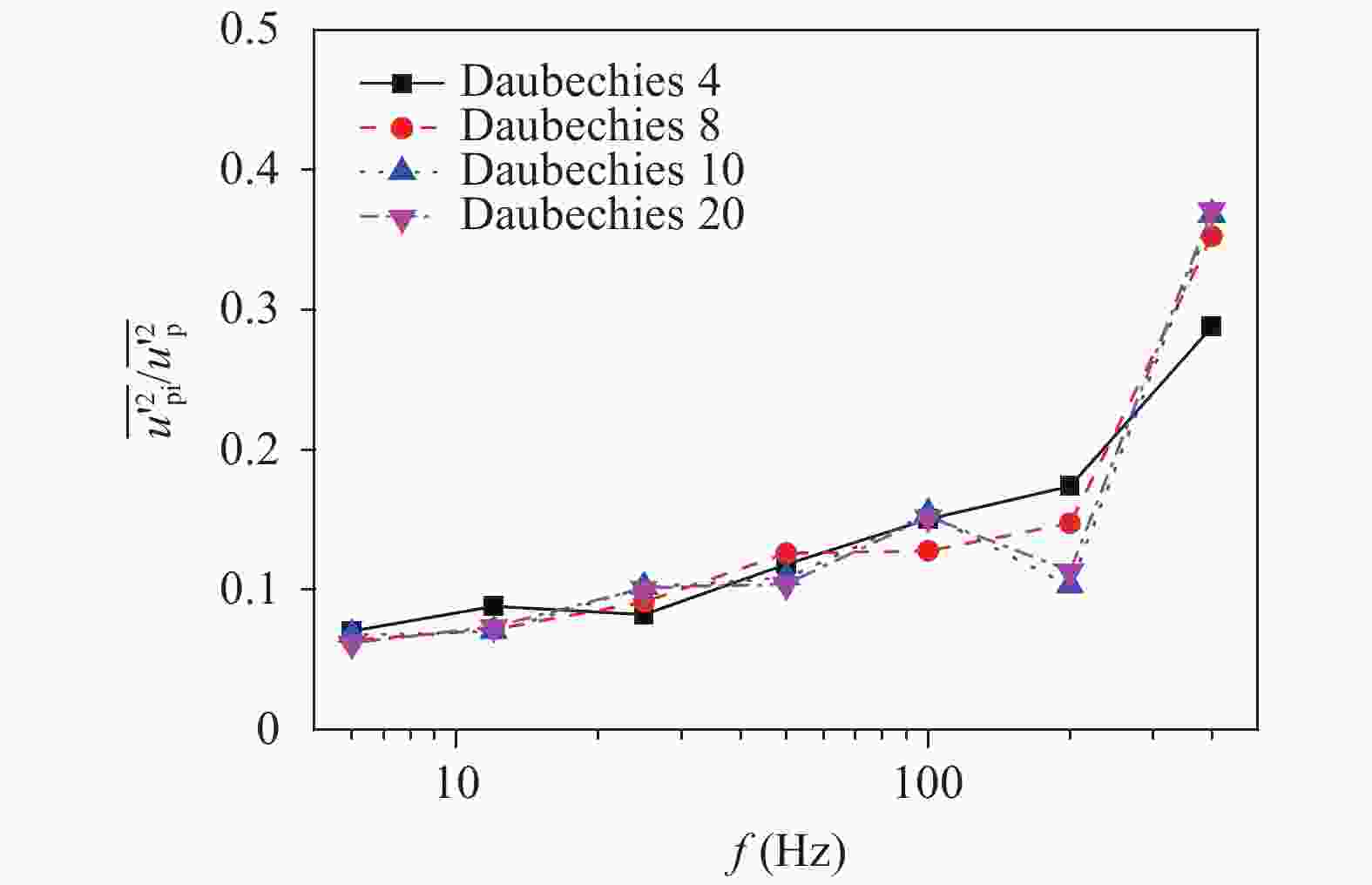
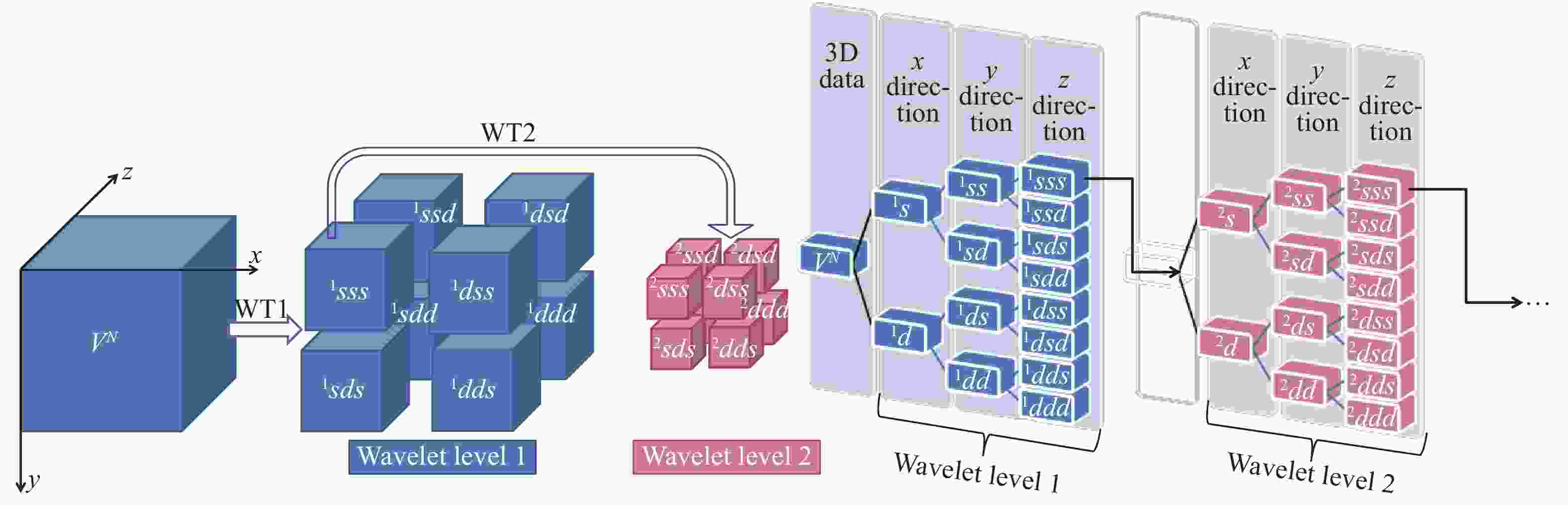
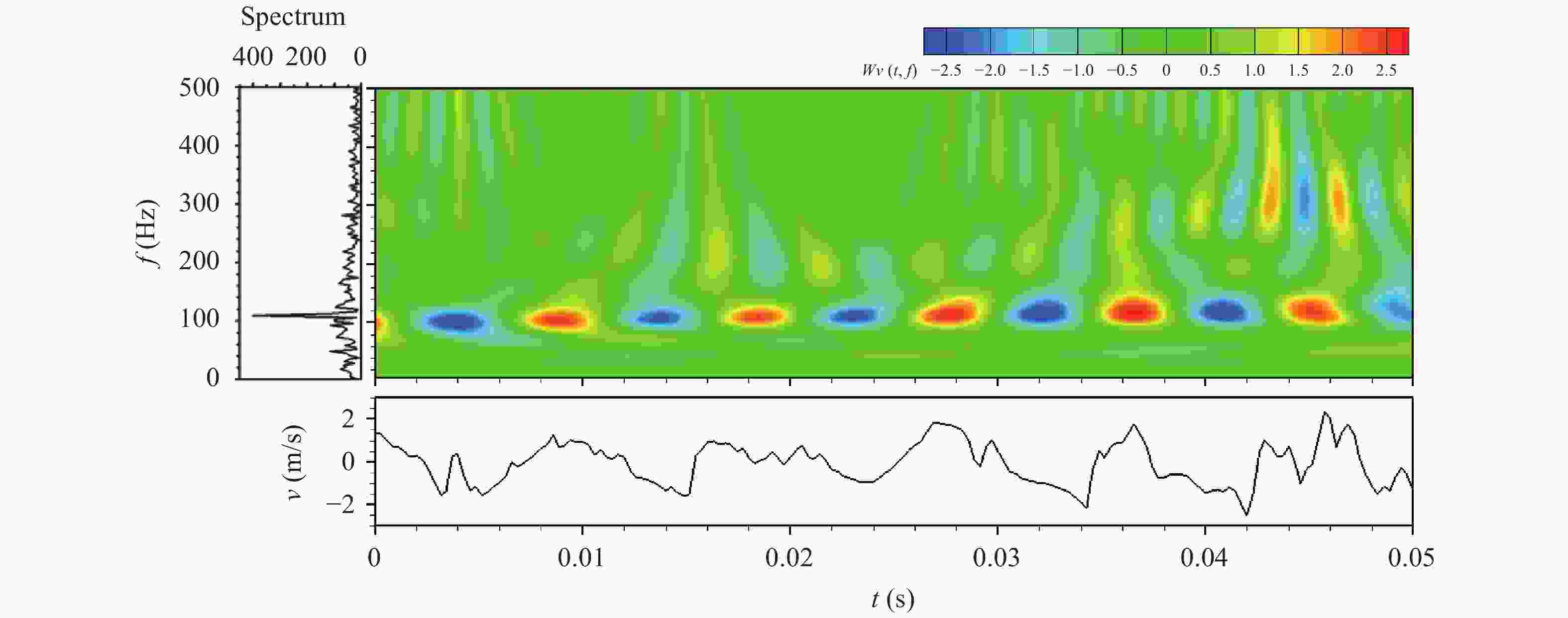
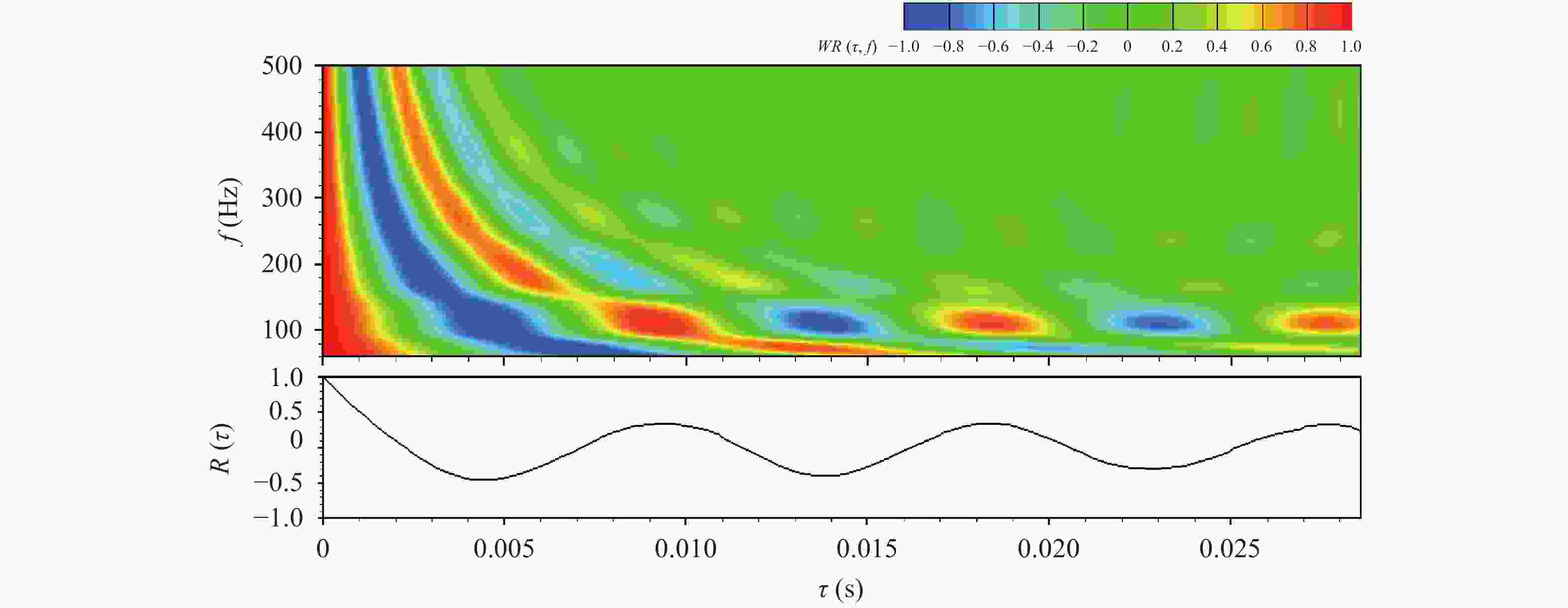
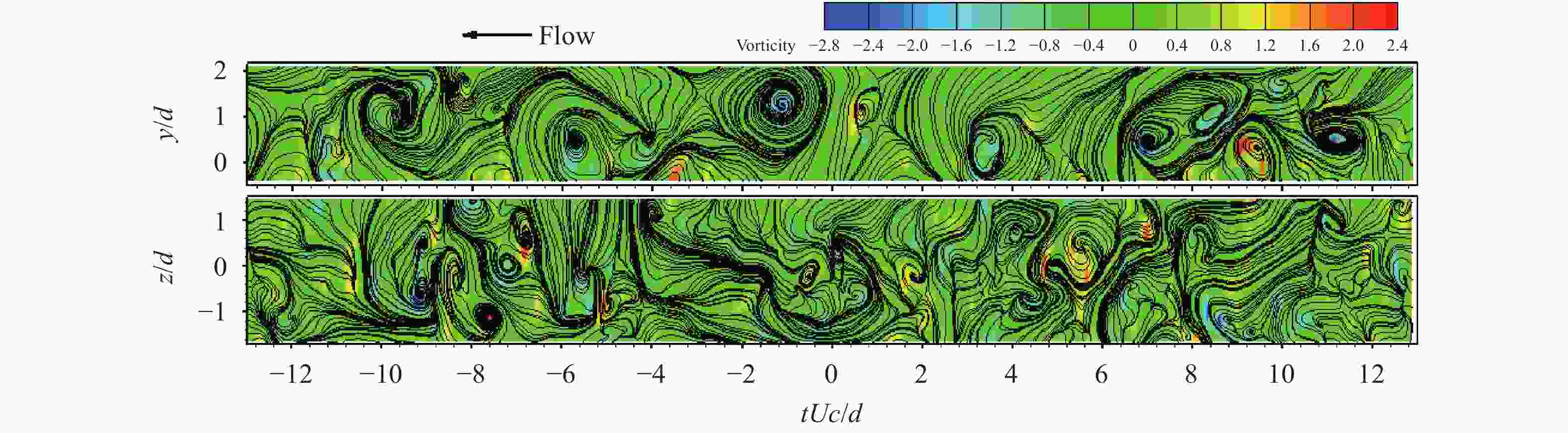
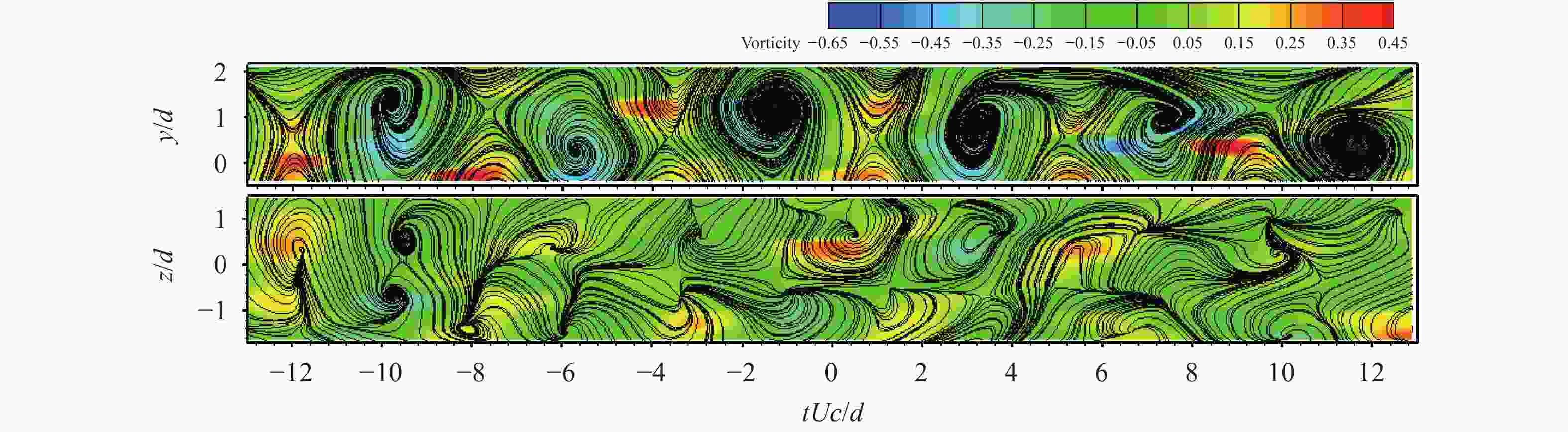
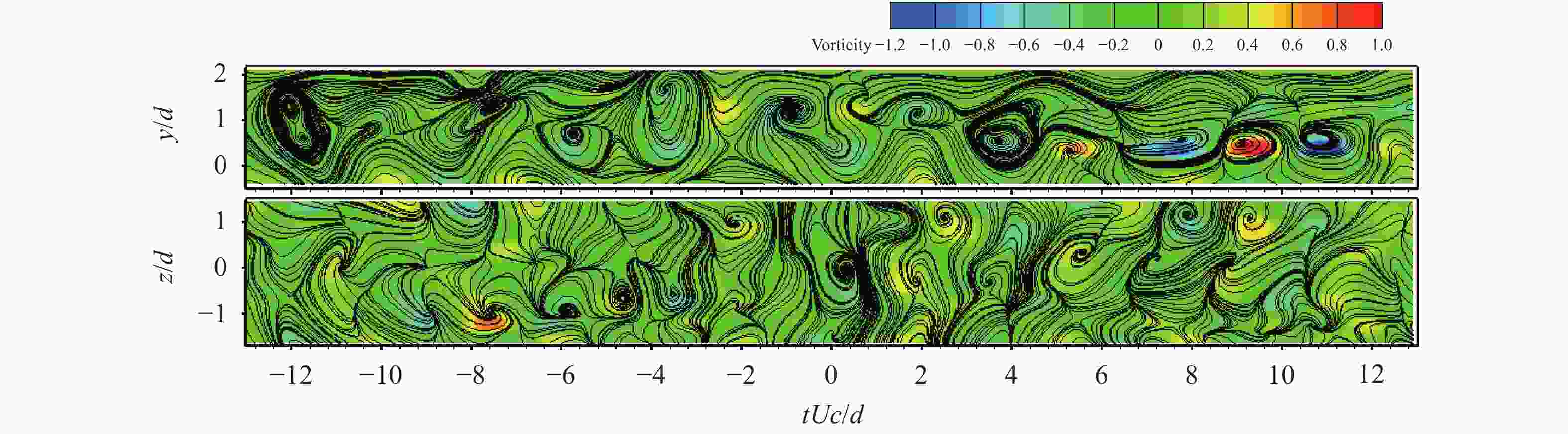
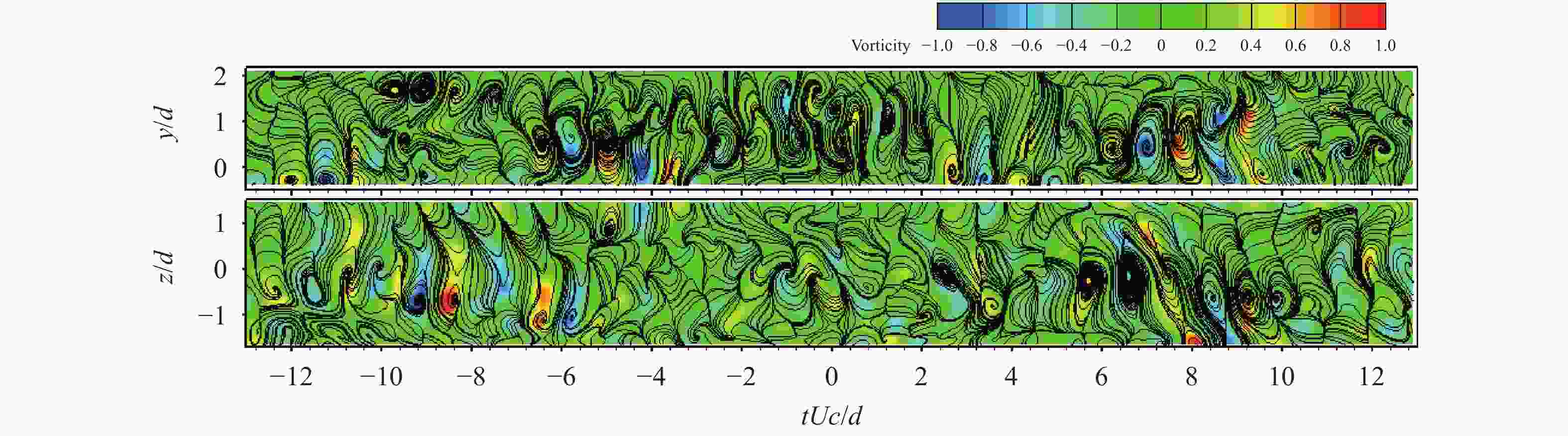
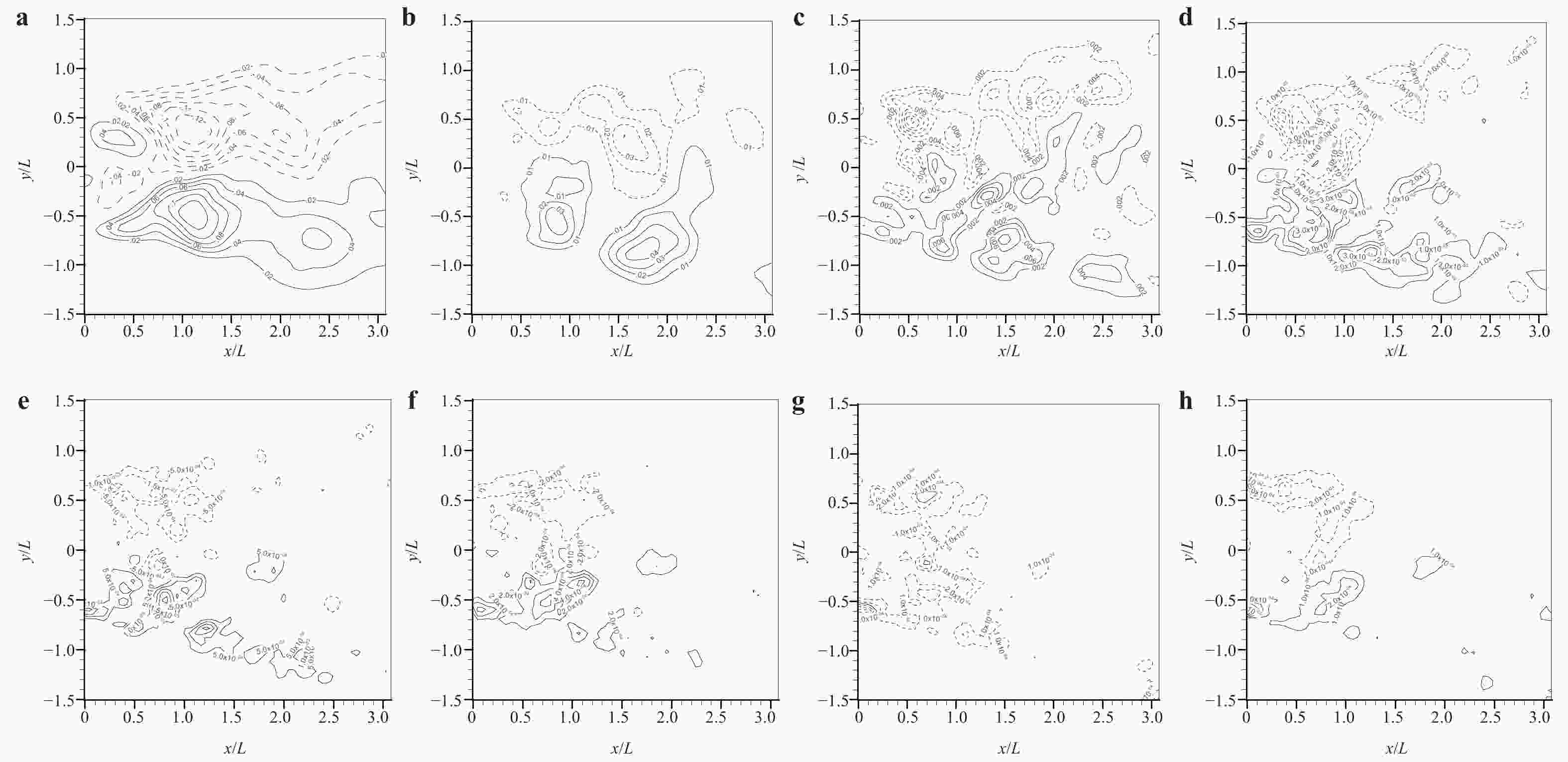
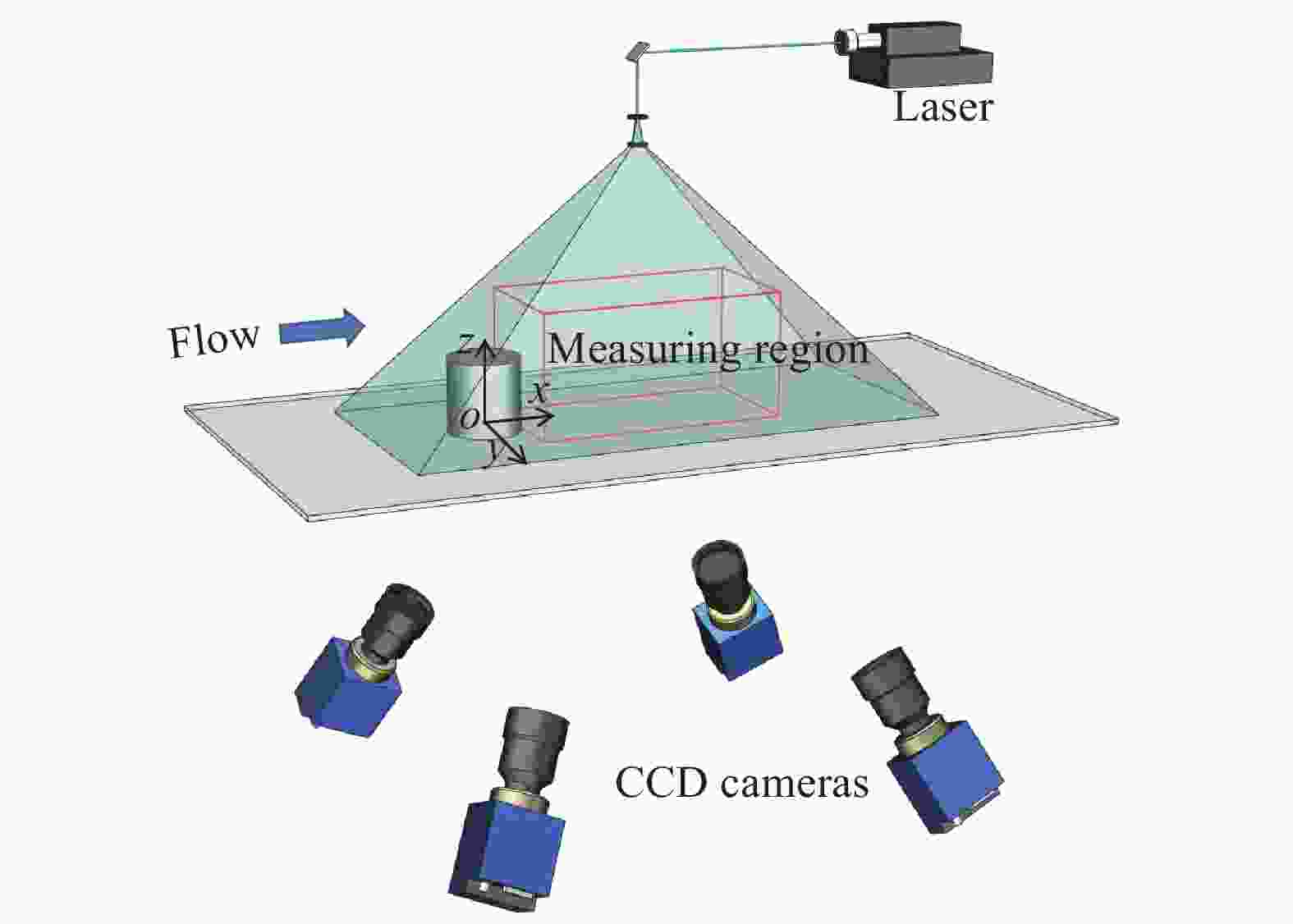
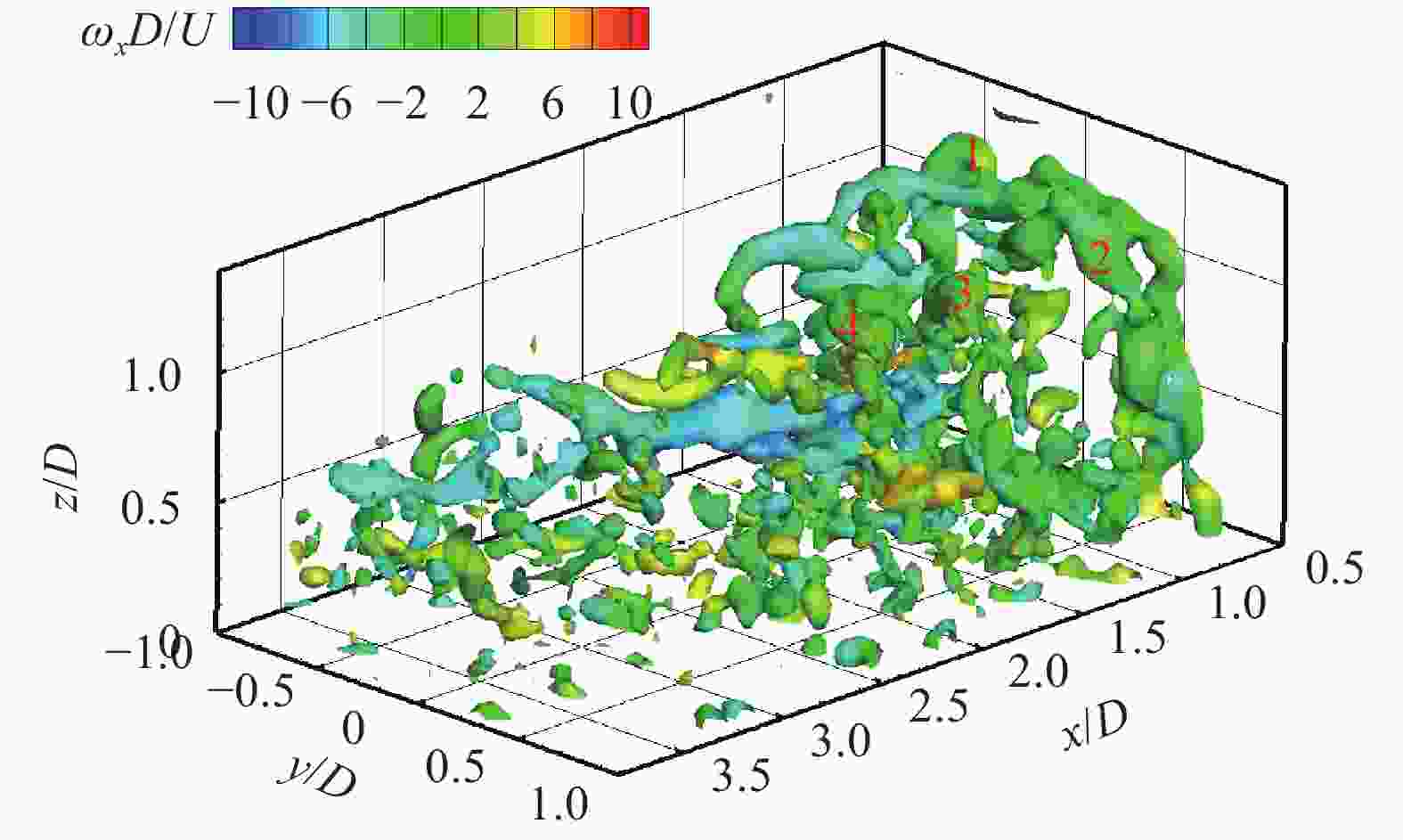
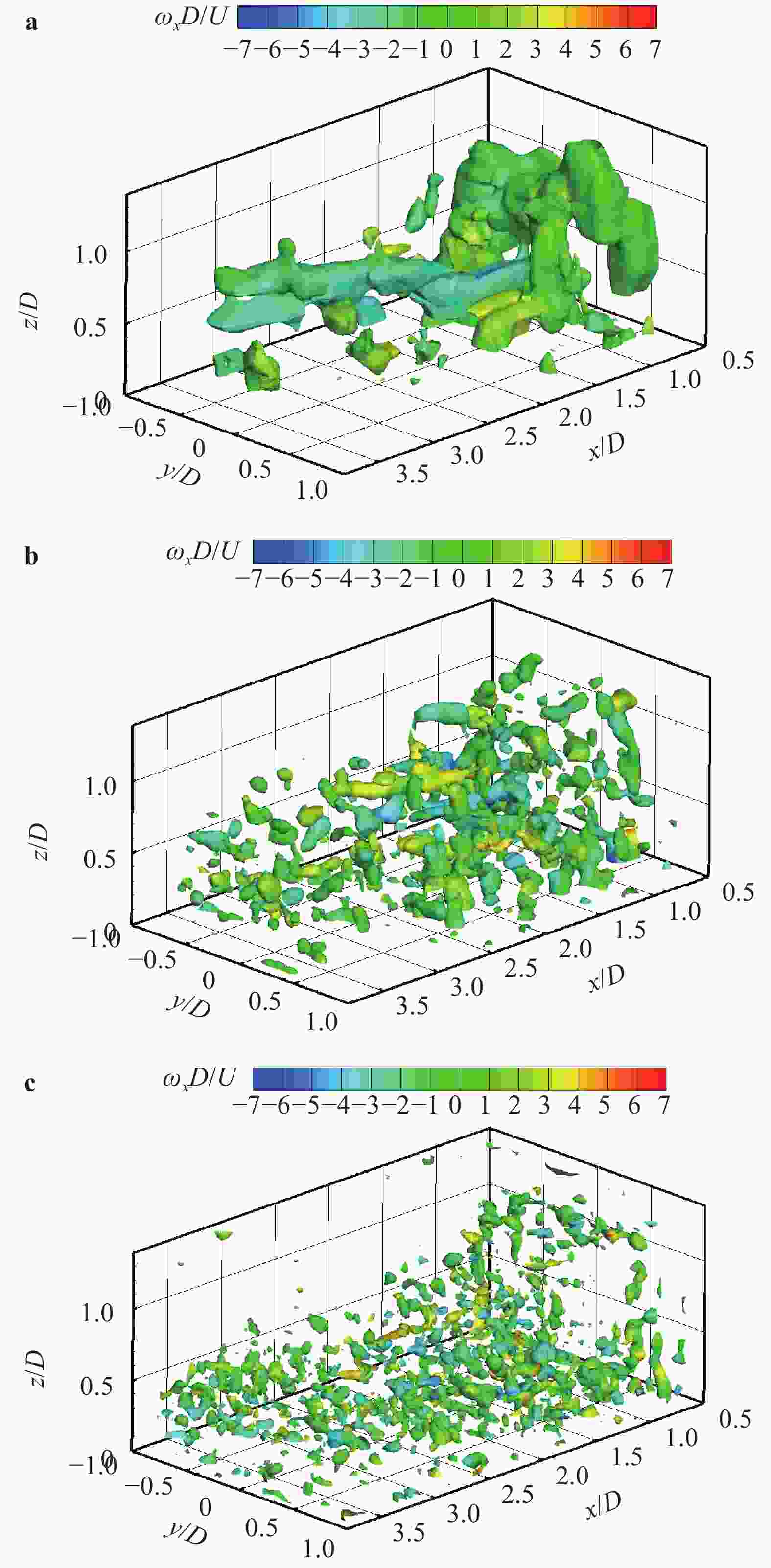
Theoretical and Applied Mechanics Letters 2020, 10(2): 98-115.
doi: 10.1016/j.taml.2020.01.017
Abstract:
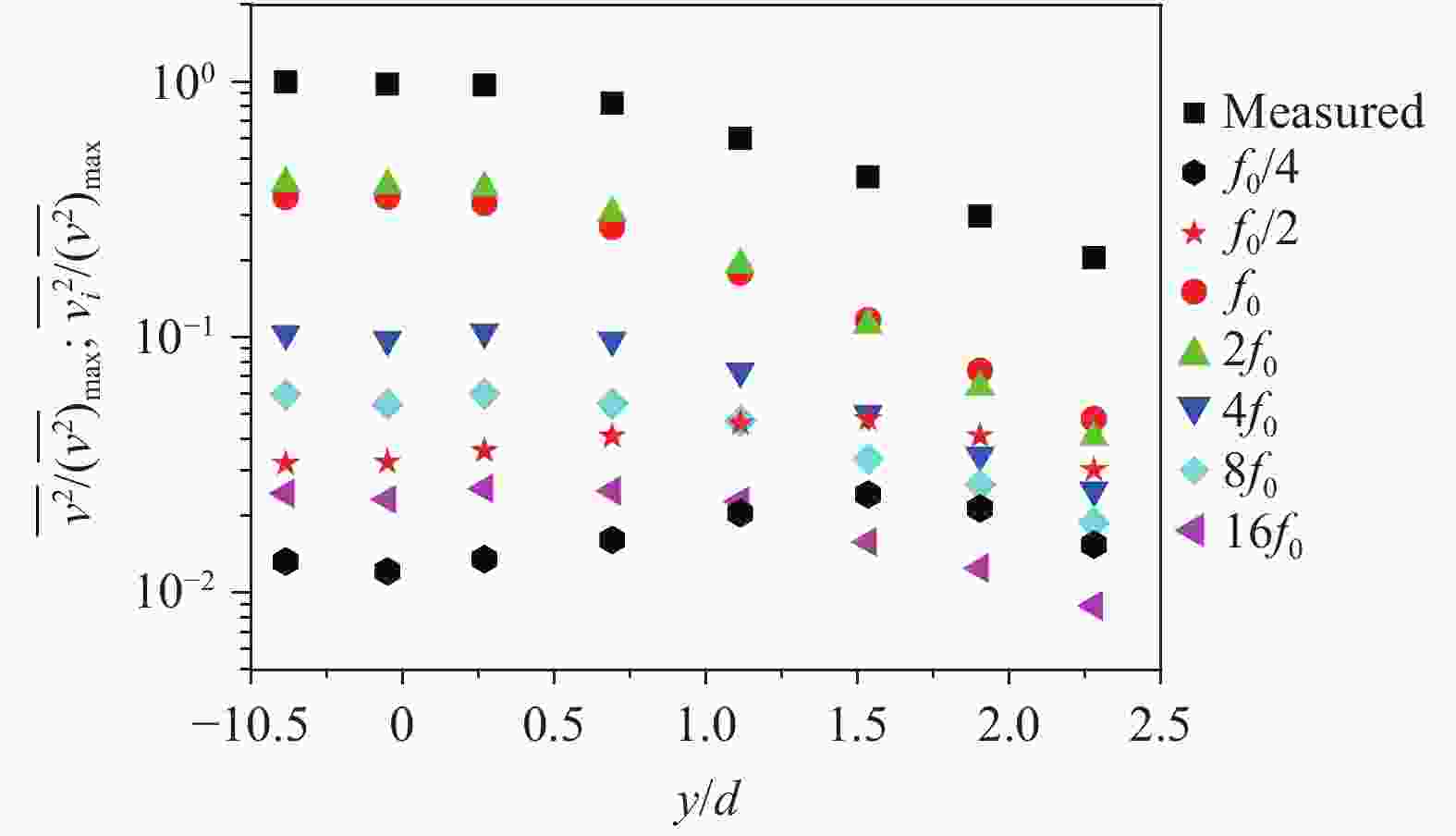
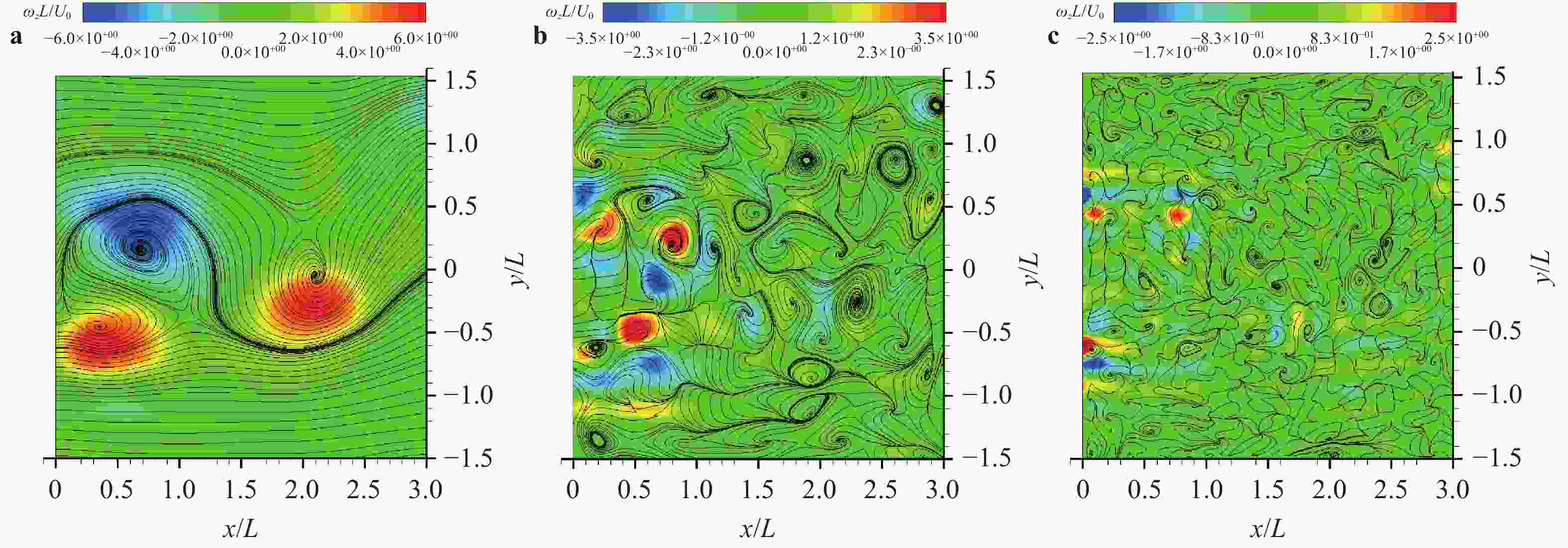
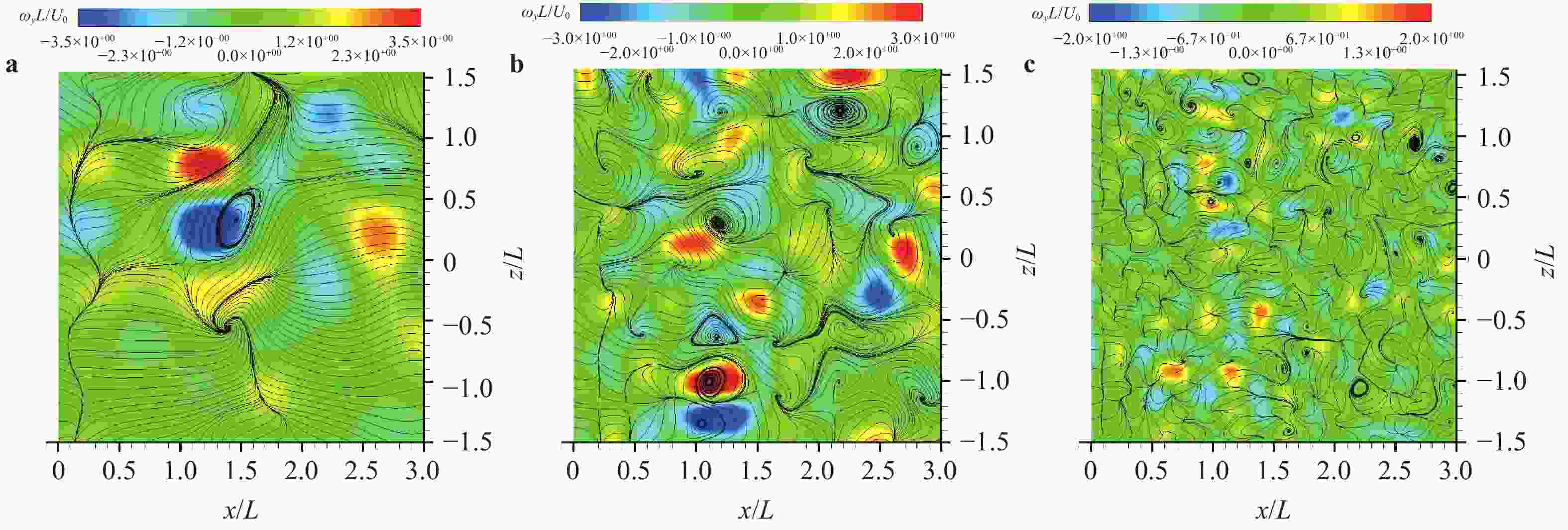
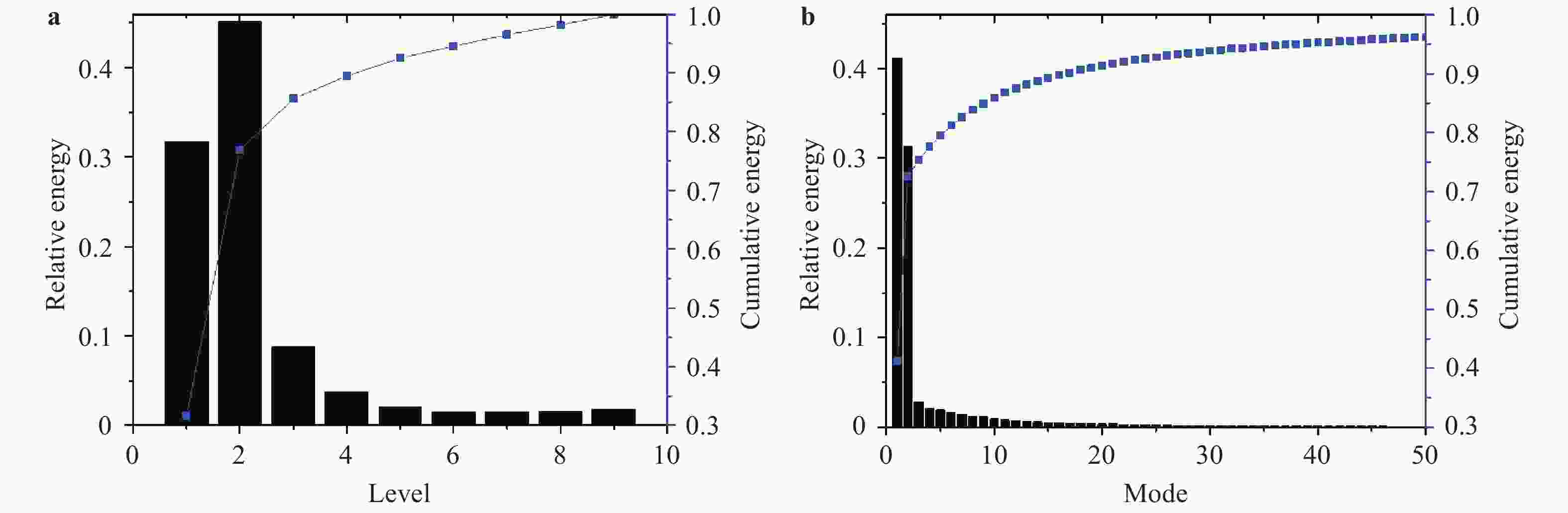
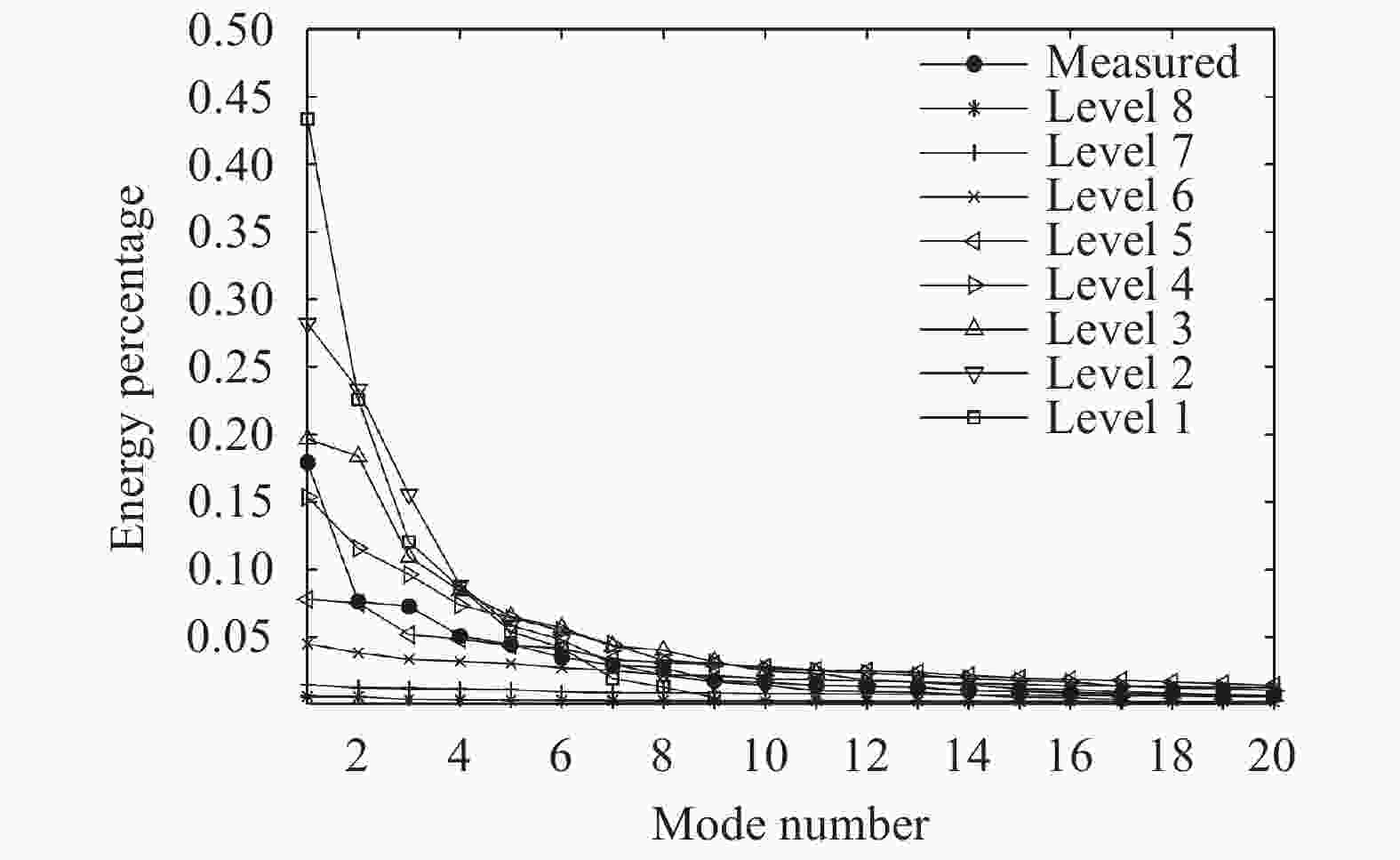
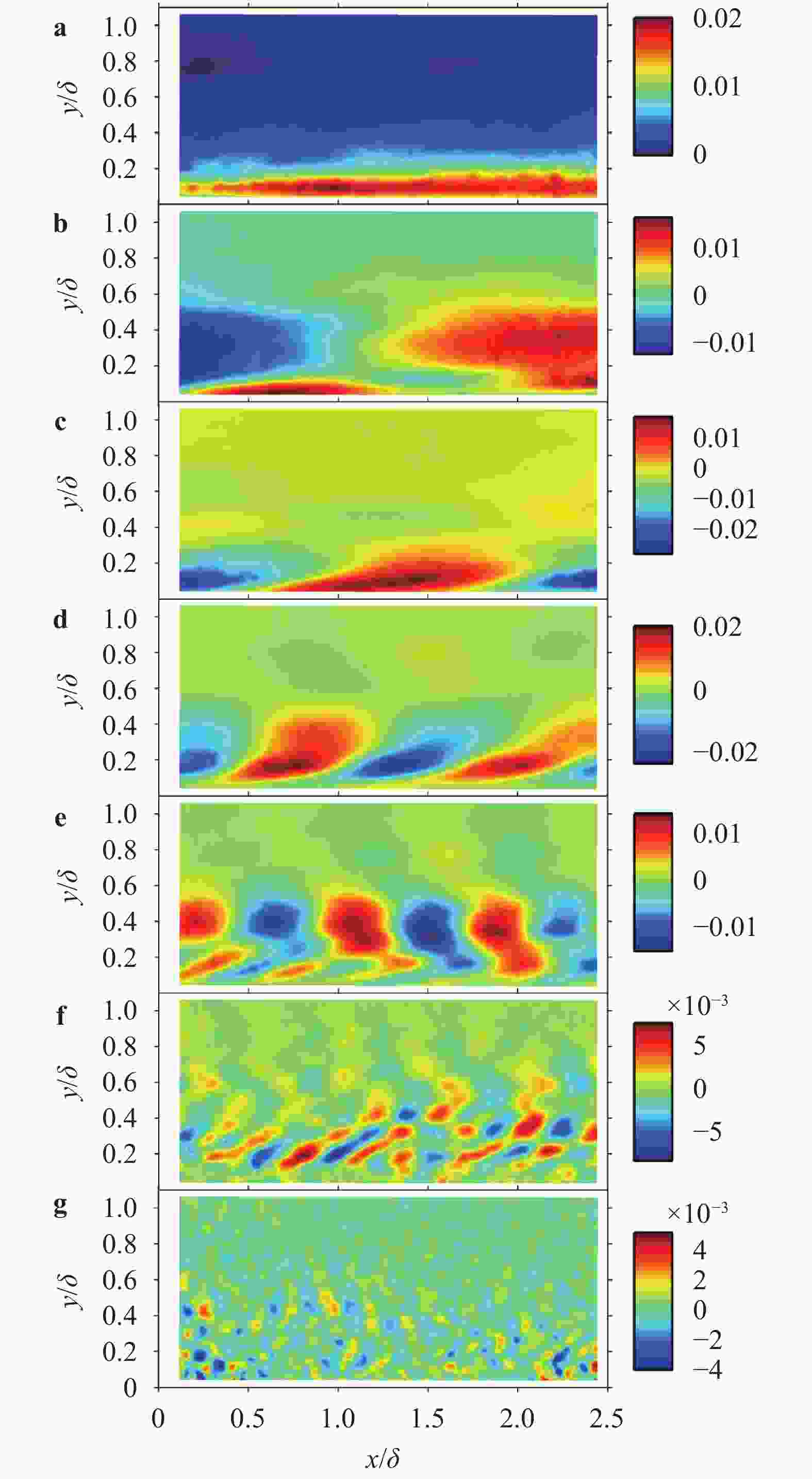
This paper first reviews the application research works of wavelet transform on the fluid mechanics. Then the theories of continuous wavelet transform and multi-dimensional orthogonal (discrete) wavelet transform, including wavelet multiresolution analysis, are introduced. At last the applications of wavelet transform on 2D and 3D turbulent wakes and turbulent boundary layer flows are described based on the hot-wire, 2D particle image velocimetry (PIV) and 3D tomographic PIV.
This paper first reviews the application research works of wavelet transform on the fluid mechanics. Then the theories of continuous wavelet transform and multi-dimensional orthogonal (discrete) wavelet transform, including wavelet multiresolution analysis, are introduced. At last the applications of wavelet transform on 2D and 3D turbulent wakes and turbulent boundary layer flows are described based on the hot-wire, 2D particle image velocimetry (PIV) and 3D tomographic PIV.
 Submit a Paper
Submit a Paper
 Subscription
Subscription
News
MORE+
Call for Papers
MORE+
- Crossing-Mechanics Driven by Big Data
- Machine learning in the fluid mechanics research of wind energy
- Mechanics of Origami/Kirigami structures and metamaterials
- New insights and perspectives on impact biomechanics for human tissues: from injury prevention, protection to protective equipment
- Environmental Mechanics for Extreme Natural Events