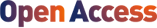Institute of Mechanics,
Chinese Academy of Sciences
2019 Vol.9(6)
Theoretical and Applied Mechanics Letters 2019, 9(6): 339-352.
doi: 10.1016/j.taml.2019.06.001
Abstract:
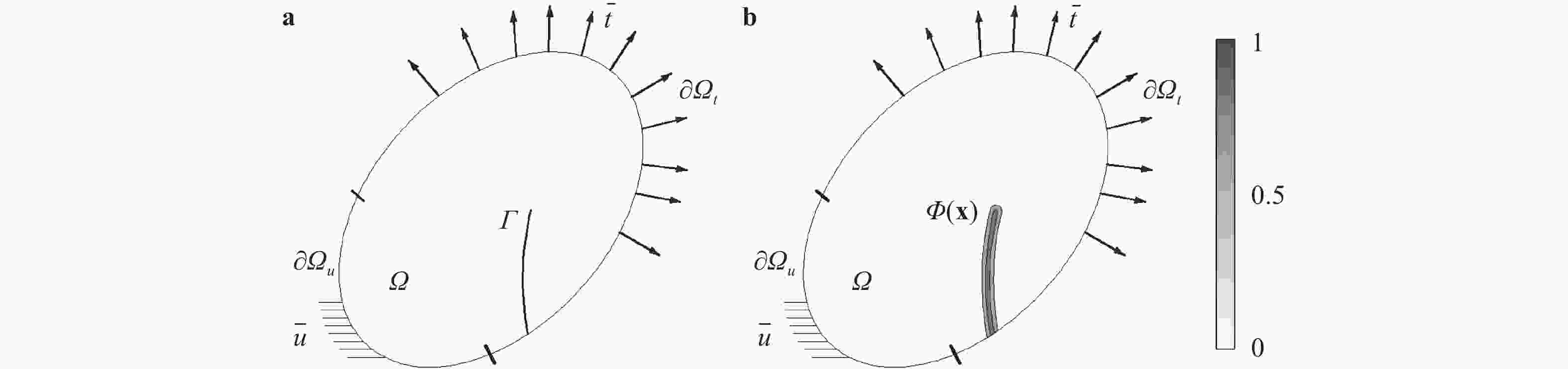
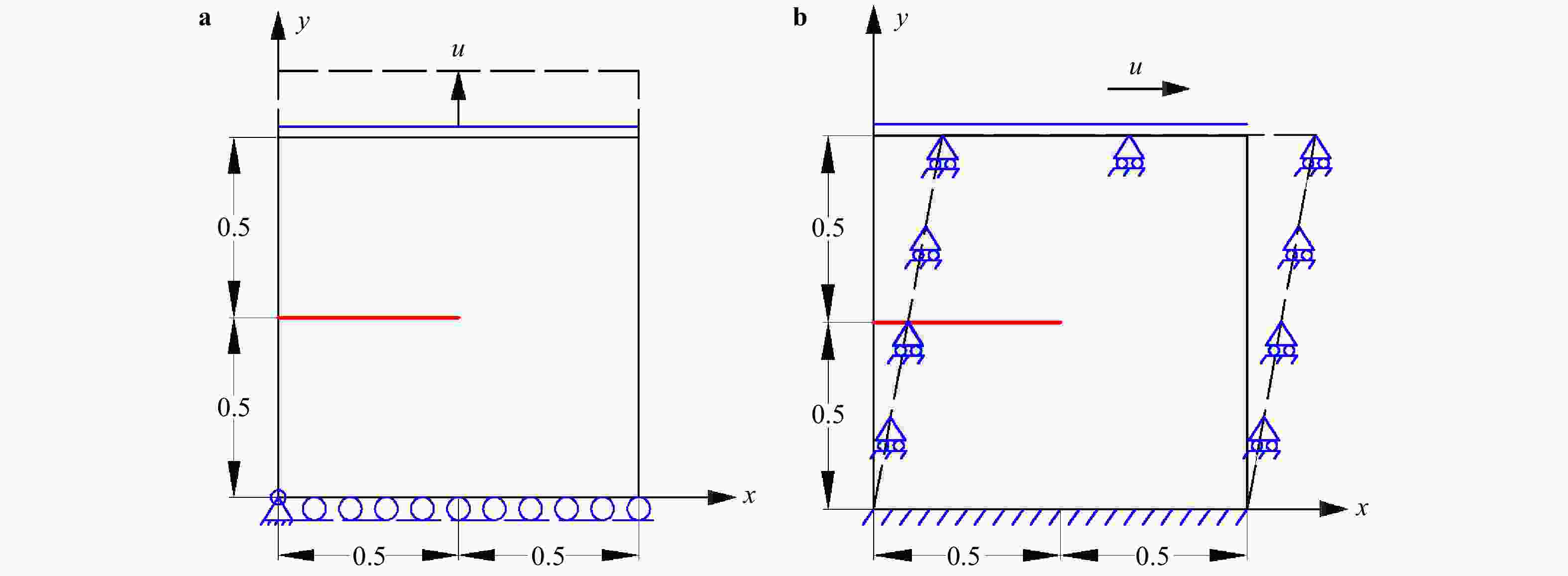
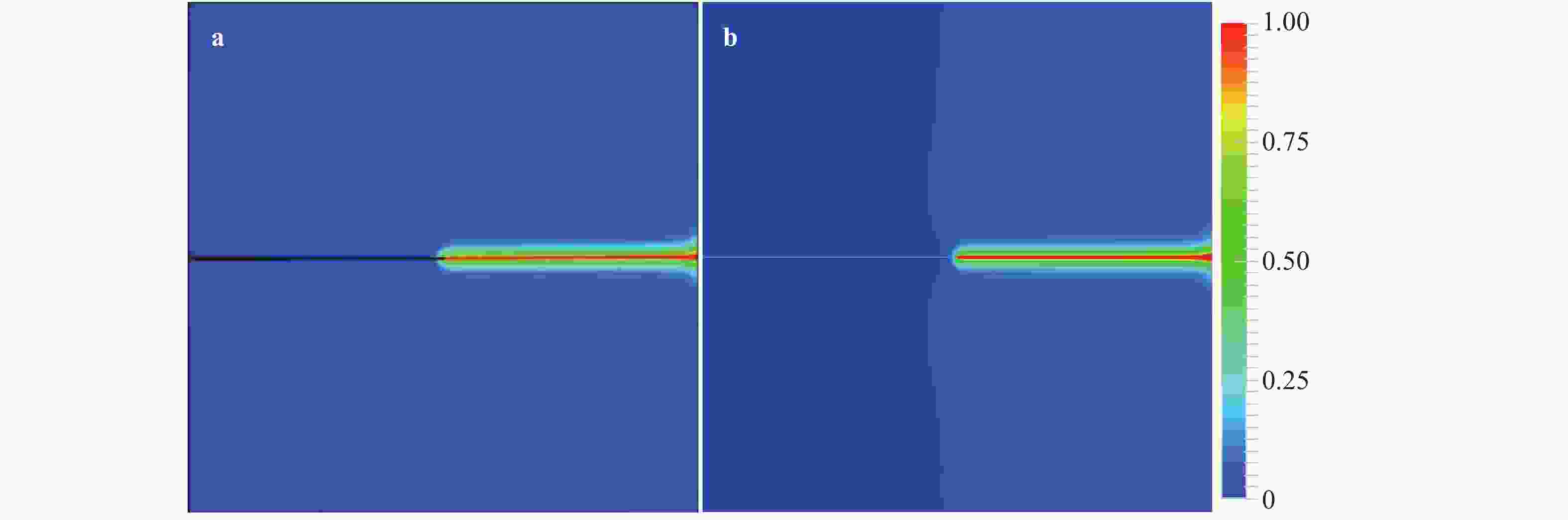
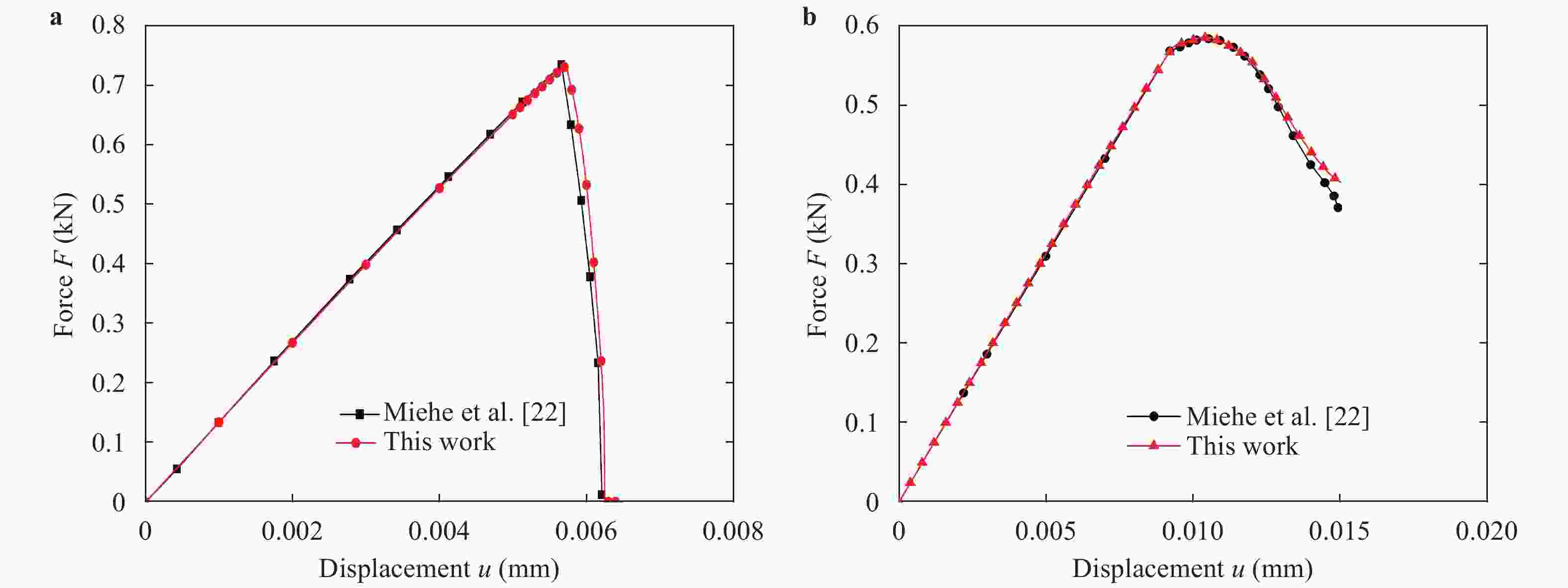
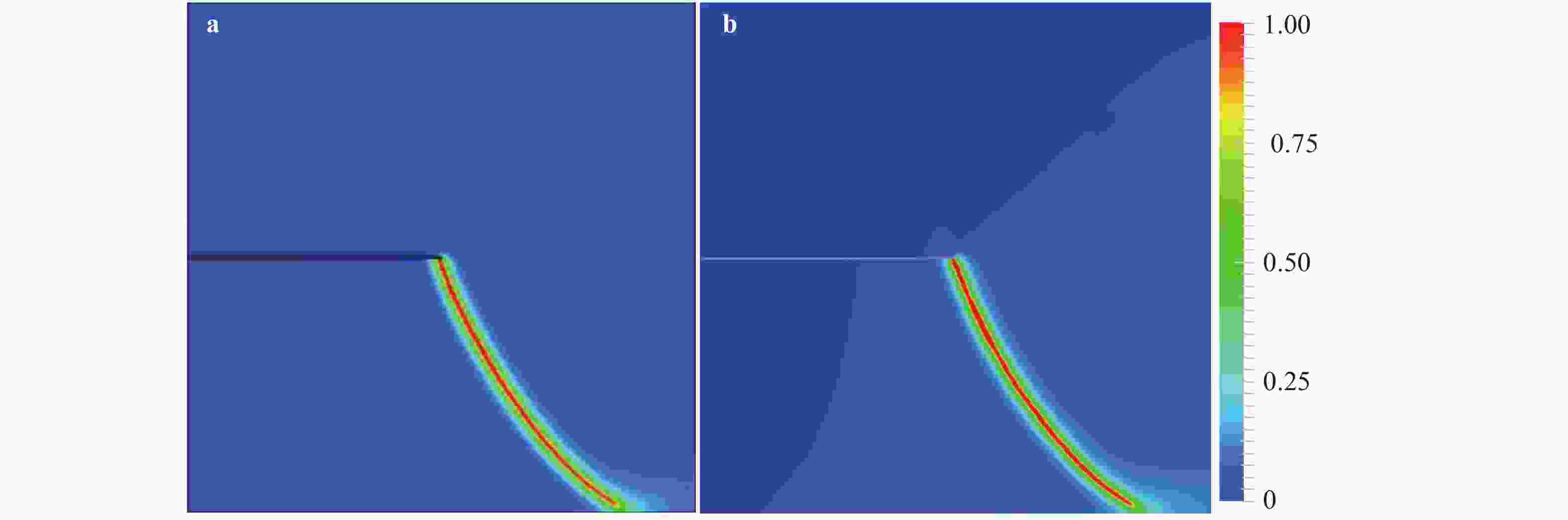
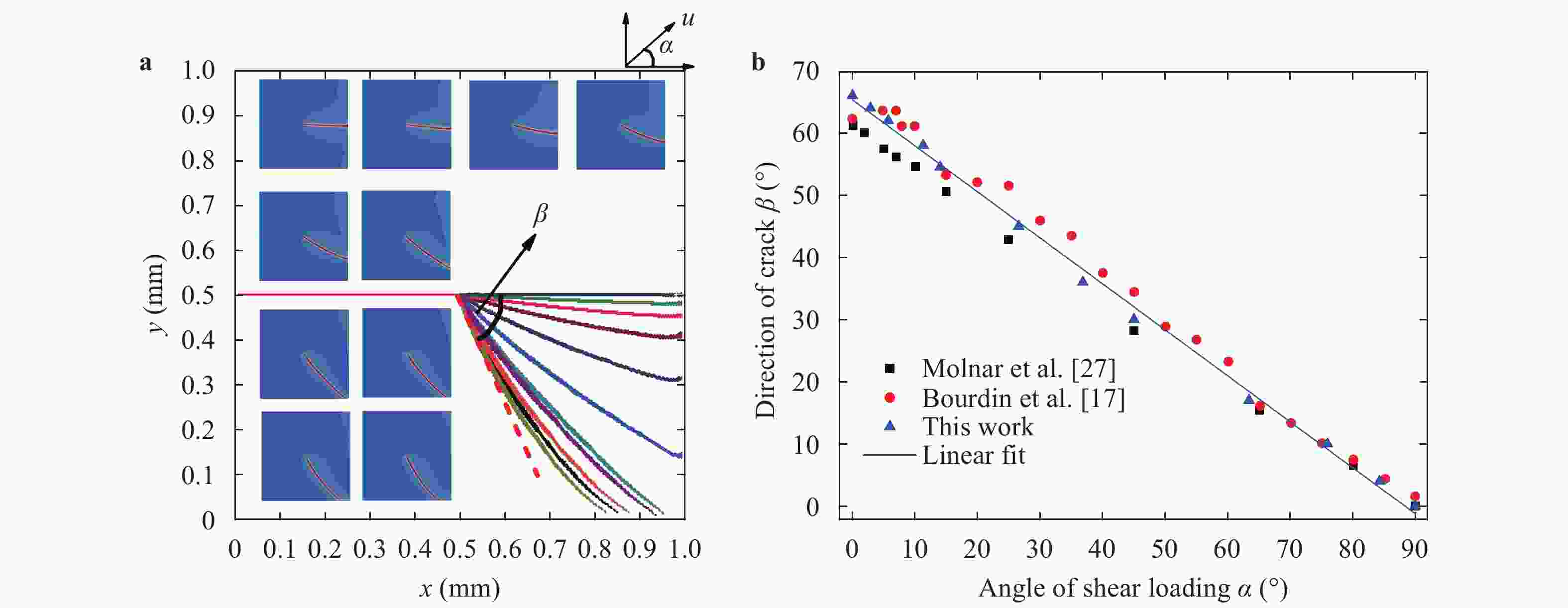
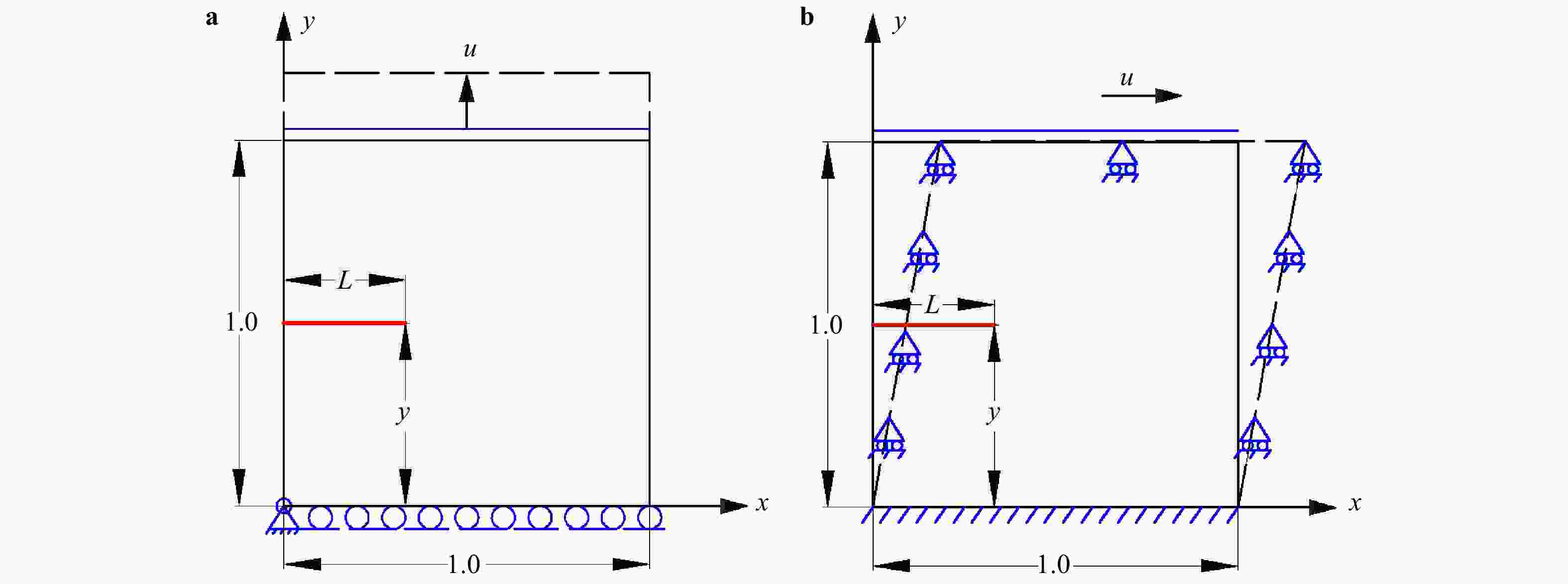
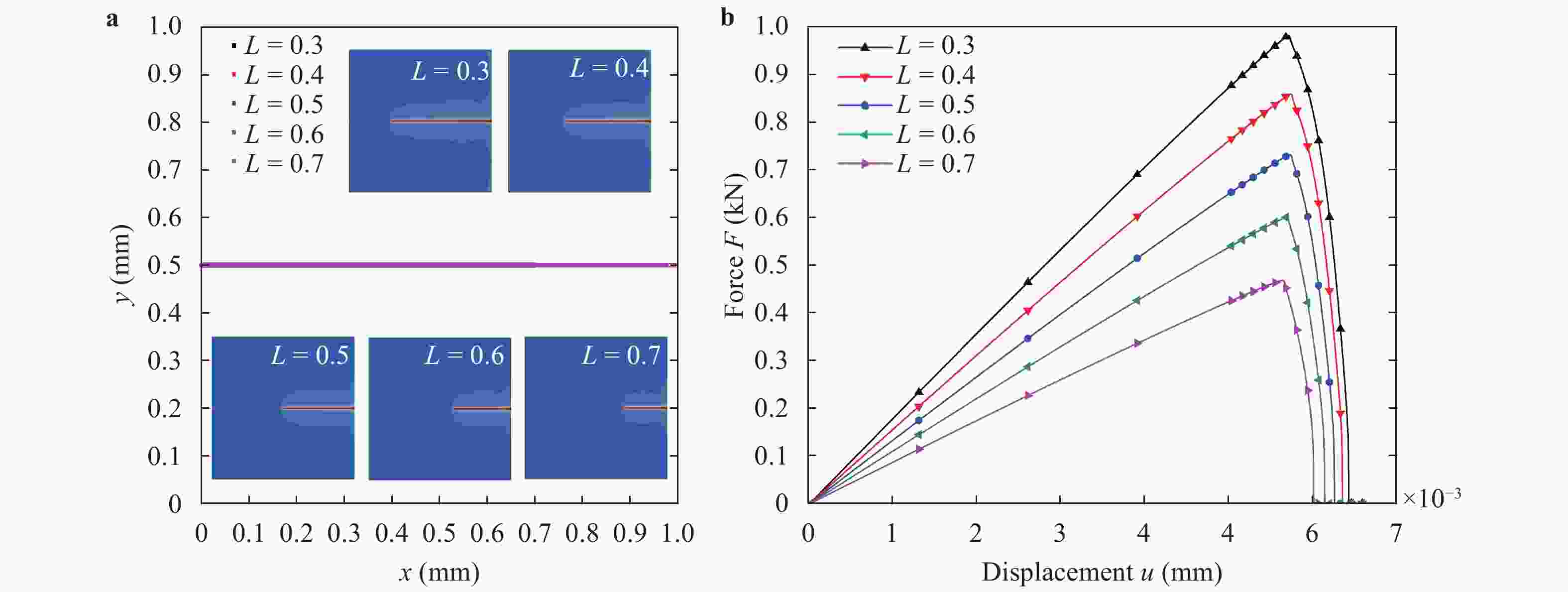
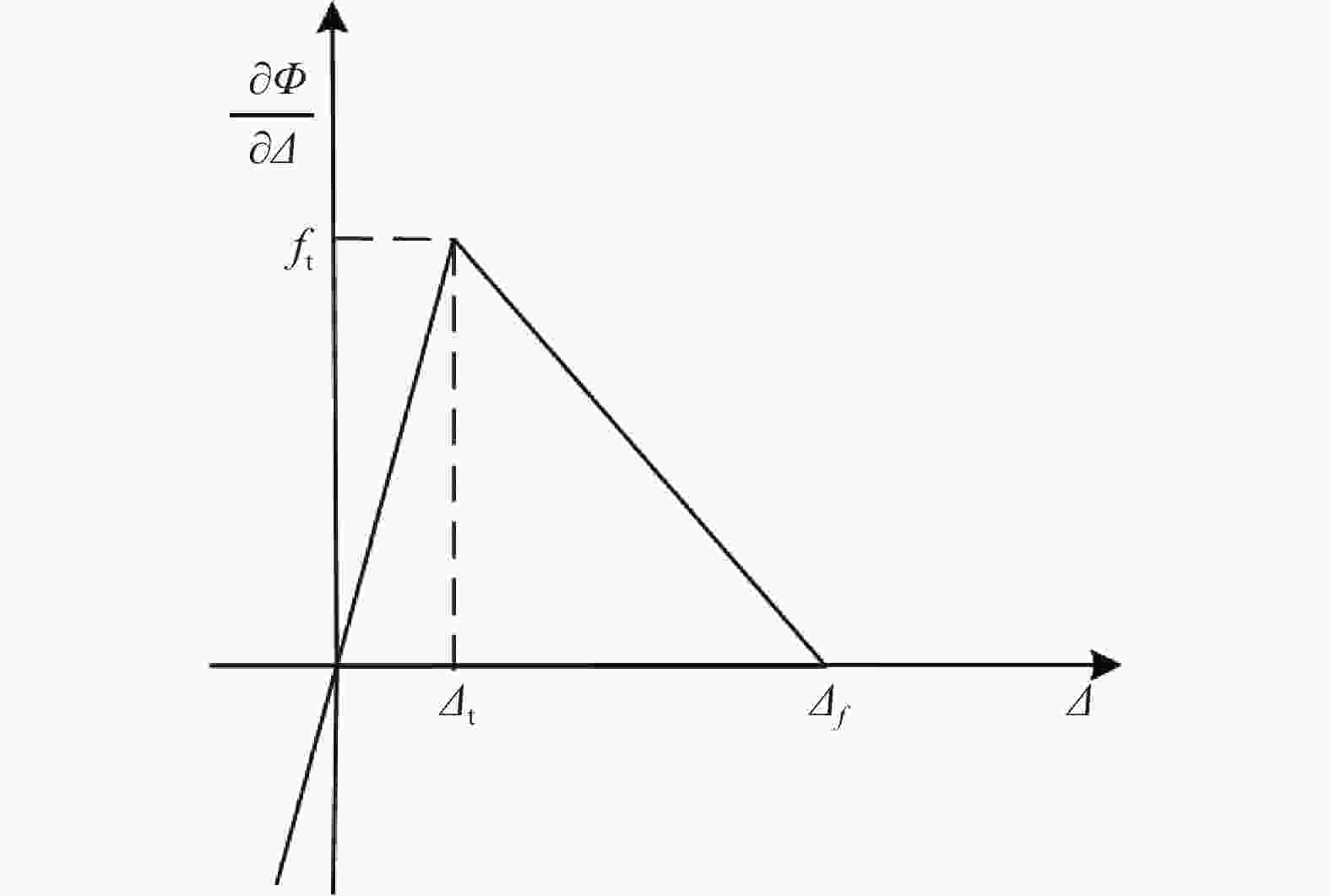
To overcome the difficulties of re-meshing and tracking the crack-tip in other computational methods for crack propagation simulations, the phase field method based on the minimum energy principle is introduced by defining a continuous phase field variable \begin{document}$\phi $\end{document} ![]()
![]()
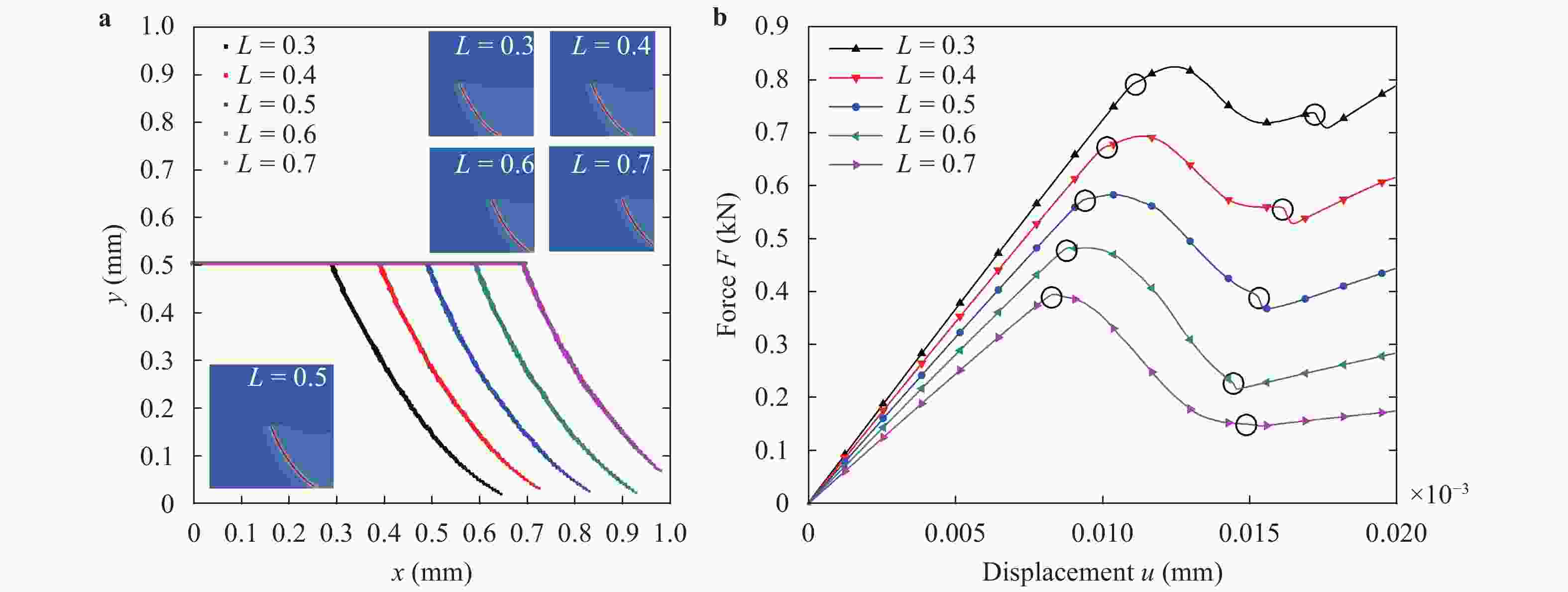
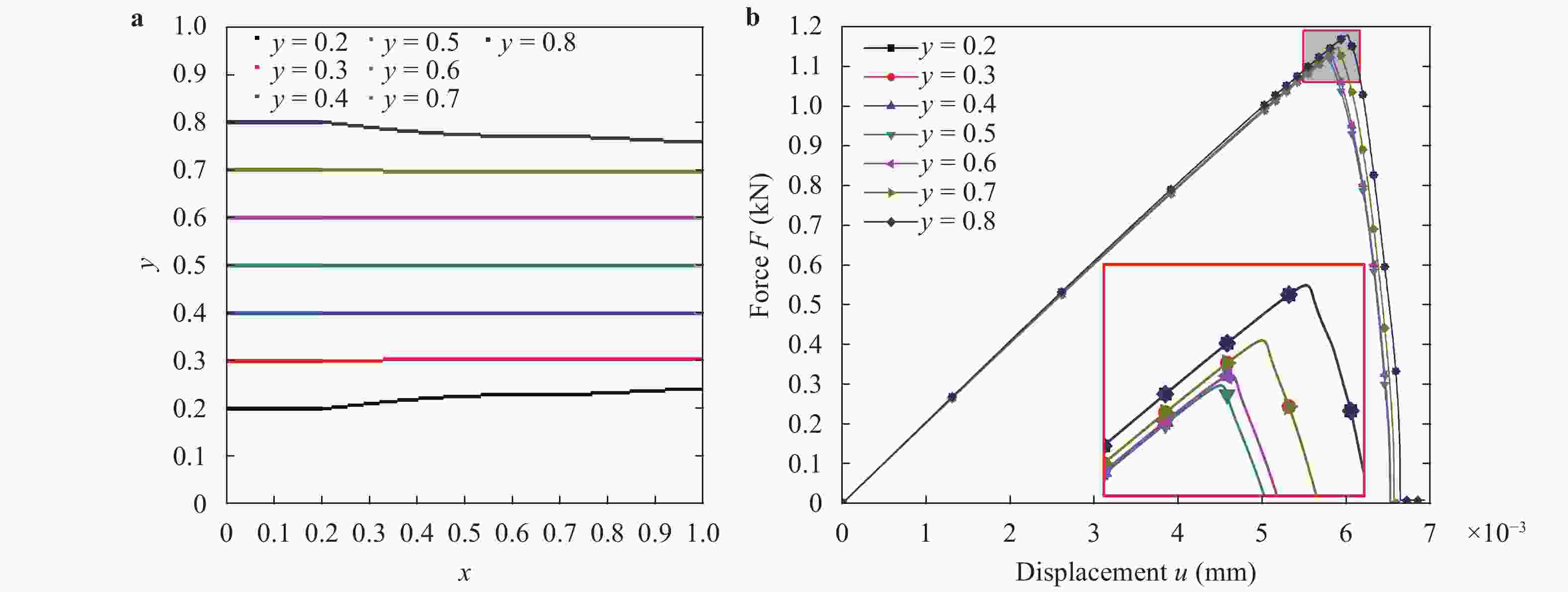
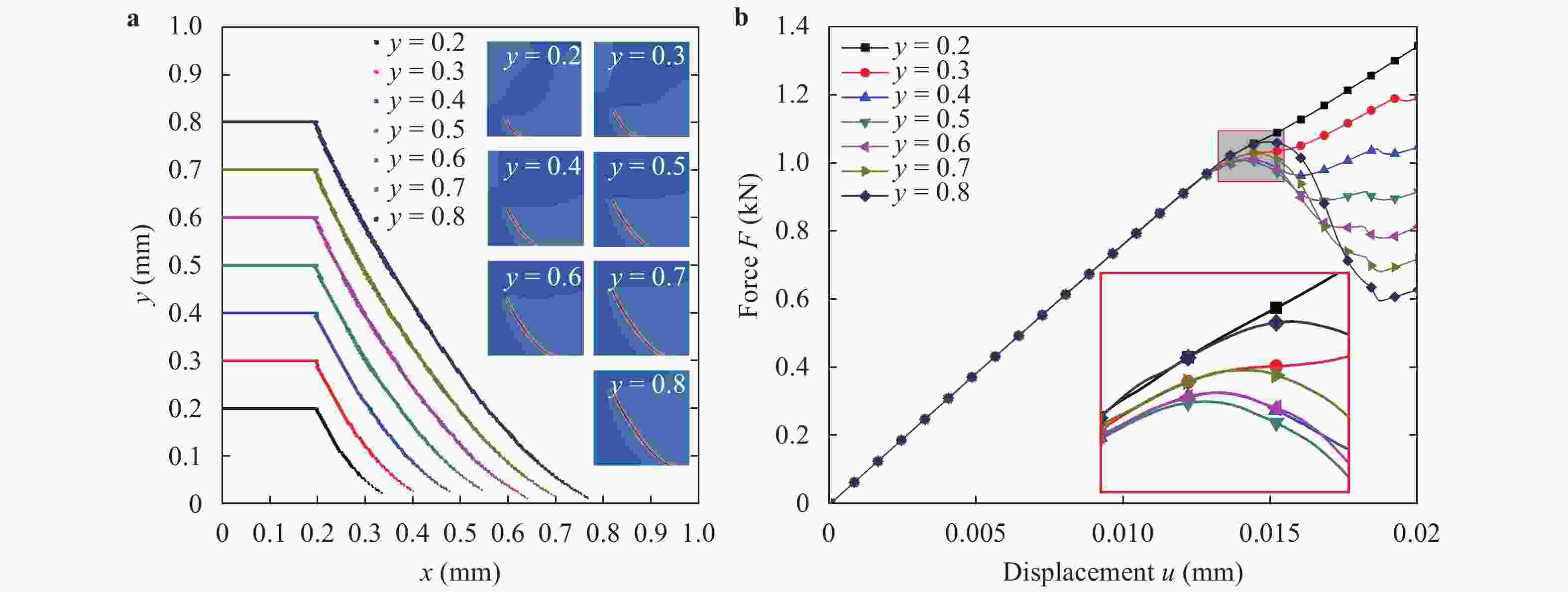
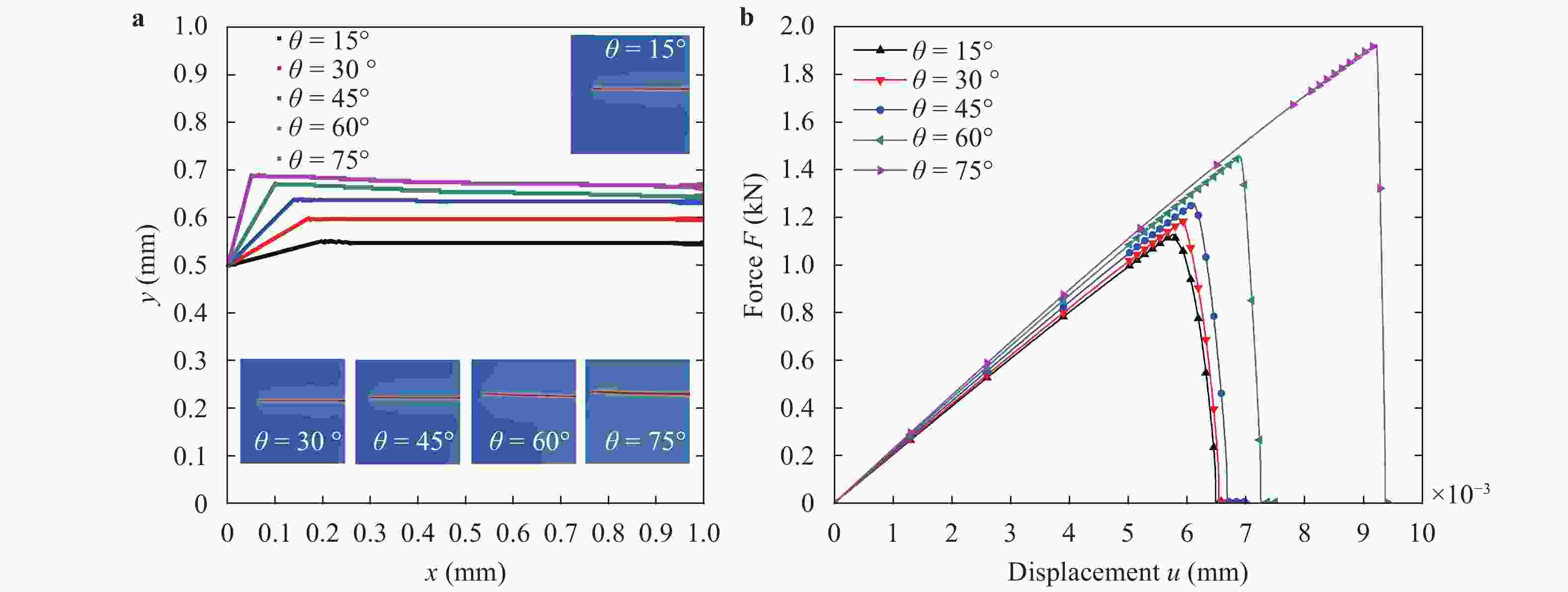
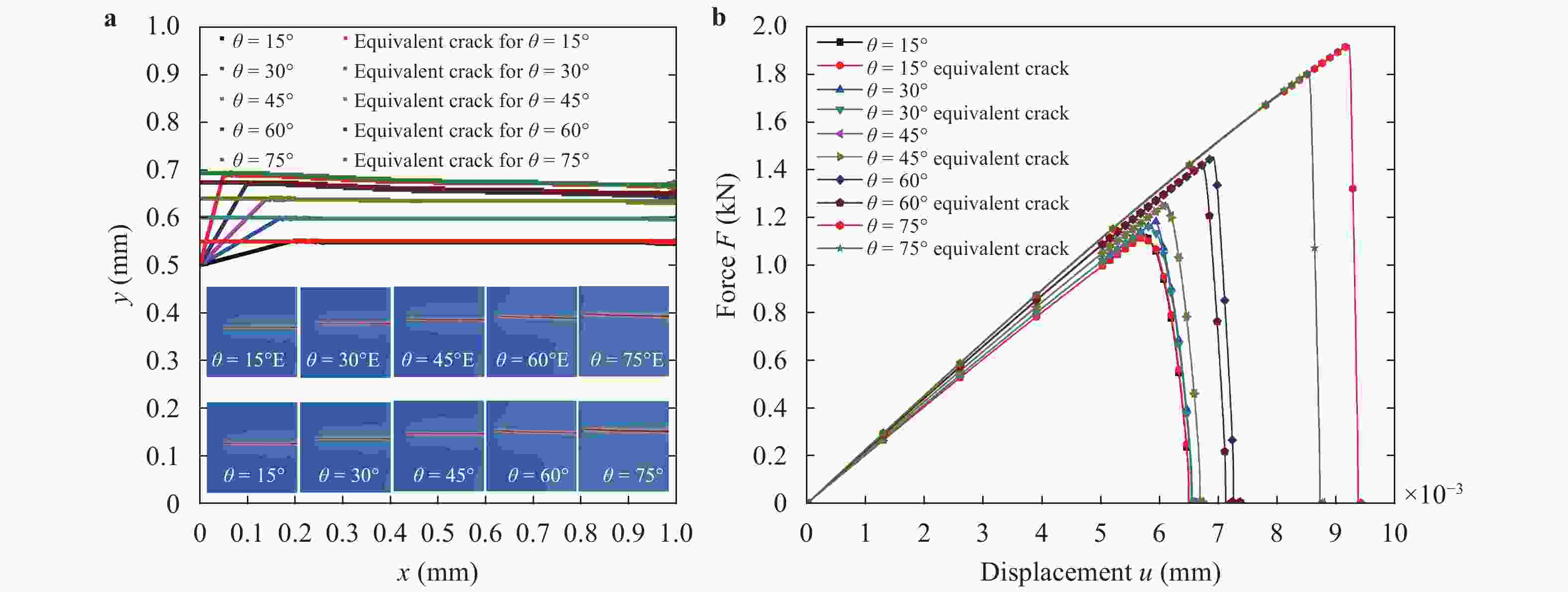
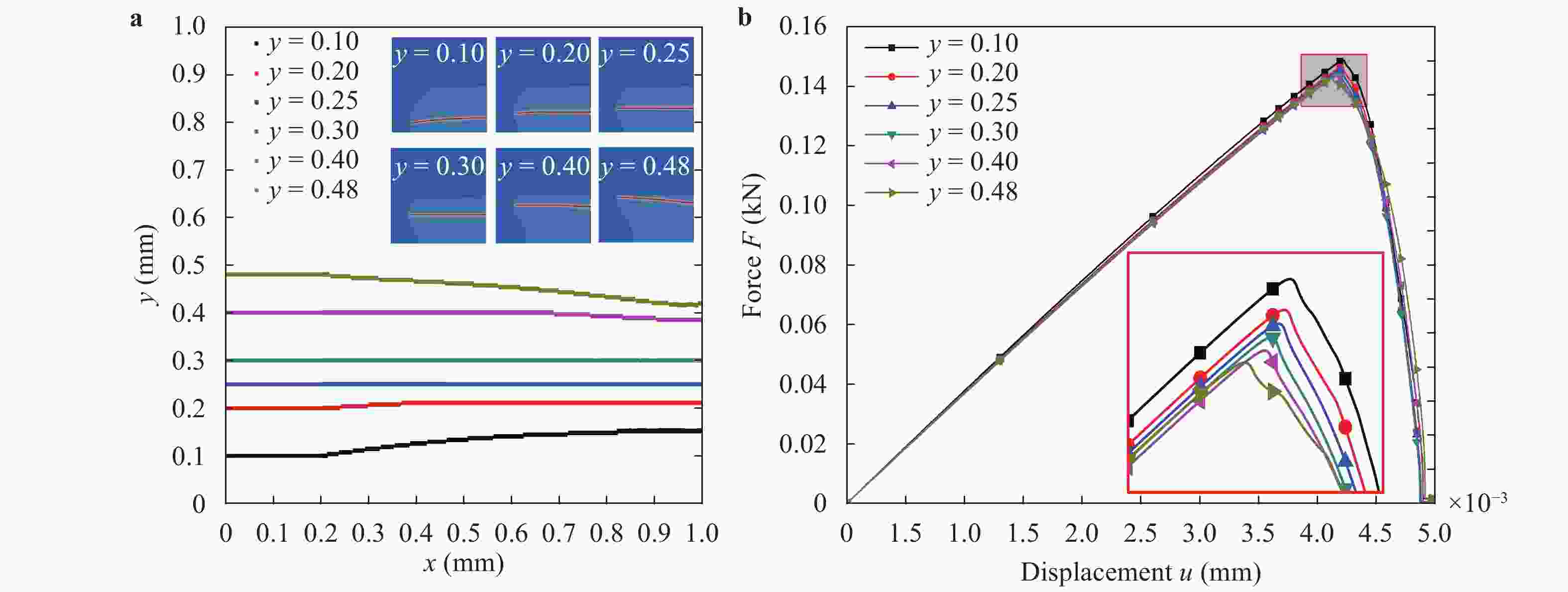
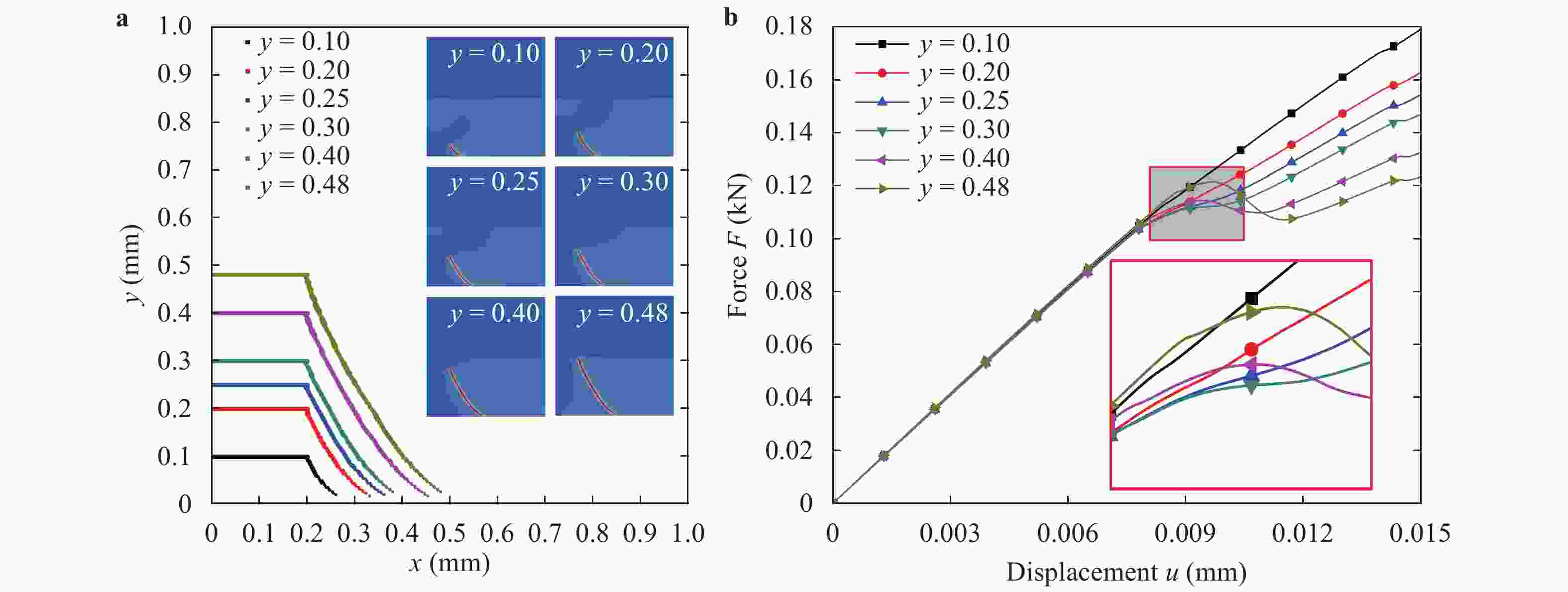
(x)∈[0,1] to characterize discontinuous cracks in brittle materials. This method can well describe the crack initiation and propagation without assuming the shape, size and orientation of the initial crack in advance. In this paper, a phase field method based on Miehe's approach [Miehe et al., Comp. Meth. App. Mech. Eng. (2010)] is applied to simulate different crack propagation problems in two-dimensional (2D), isotropic and linear elastic materials. The numerical implementation of the phase field method is realized within the framework of the finite element method (FEM). The validity, accuracy and efficiency of the present method are verified by comparing the numerical results with other reference results in literature. Several numerical examples are presented to show the effects of the loading type (tension and shear), boundary conditions, and initial crack location and orientation on the crack propagation path and force-displacement curve. Furthermore, for a single edge-cracked bi-material specimen, the influences of the loading type and the crack location on the crack propagation trajectory and force-displacement curve are also investigated and discussed. It is demonstrated that the phase field method is an efficient tool for the numerical simulation of the crack propagation problems in brittle elastic materials, and the corresponding results may have an important relevance for predicting and preventing possible crack propagations in engineering applications.
To overcome the difficulties of re-meshing and tracking the crack-tip in other computational methods for crack propagation simulations, the phase field method based on the minimum energy principle is introduced by defining a continuous phase field variable
Theoretical and Applied Mechanics Letters 2019, 9(6): 363-375.
doi: 10.1016/j.taml.2019.05.004
Abstract:
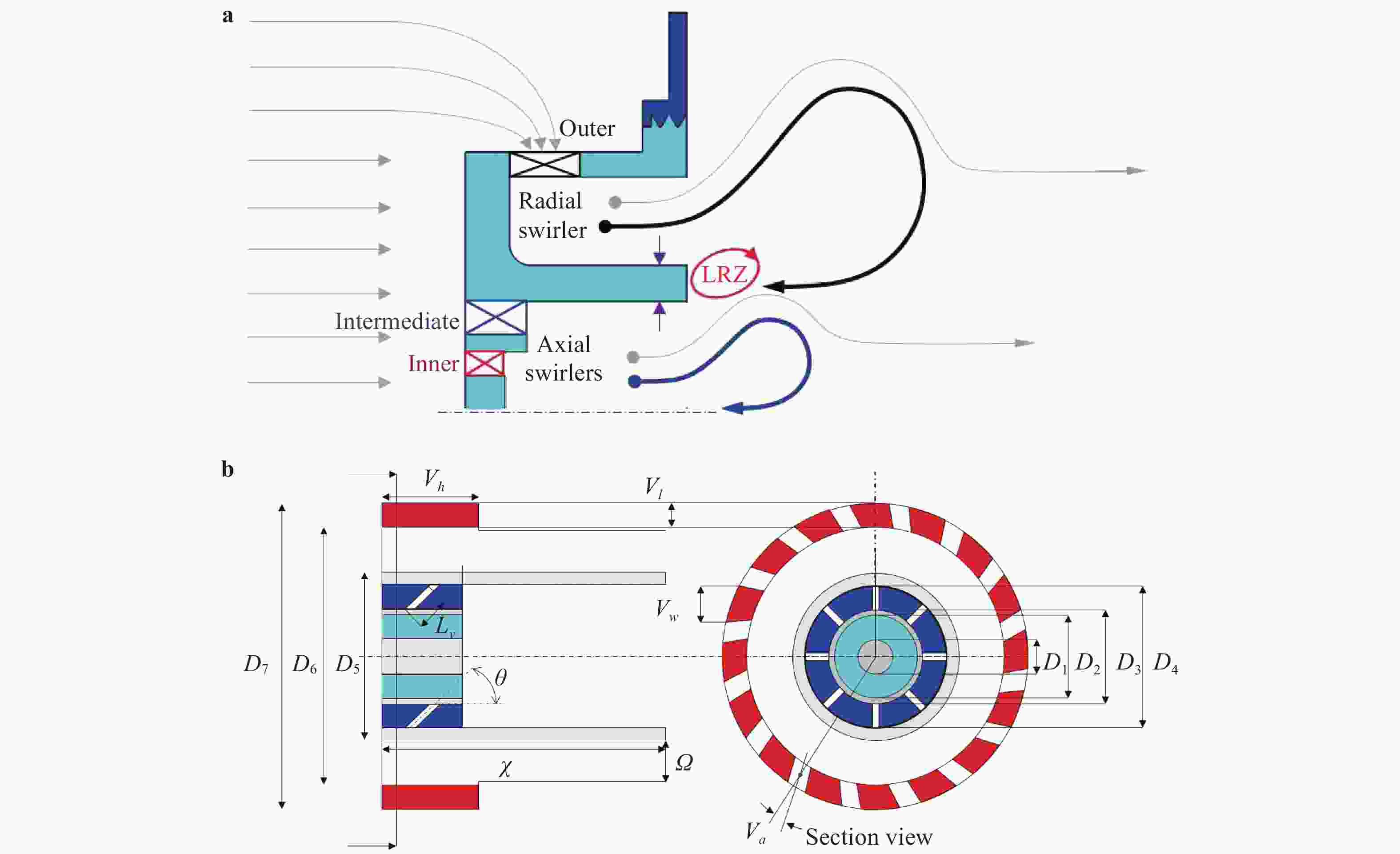
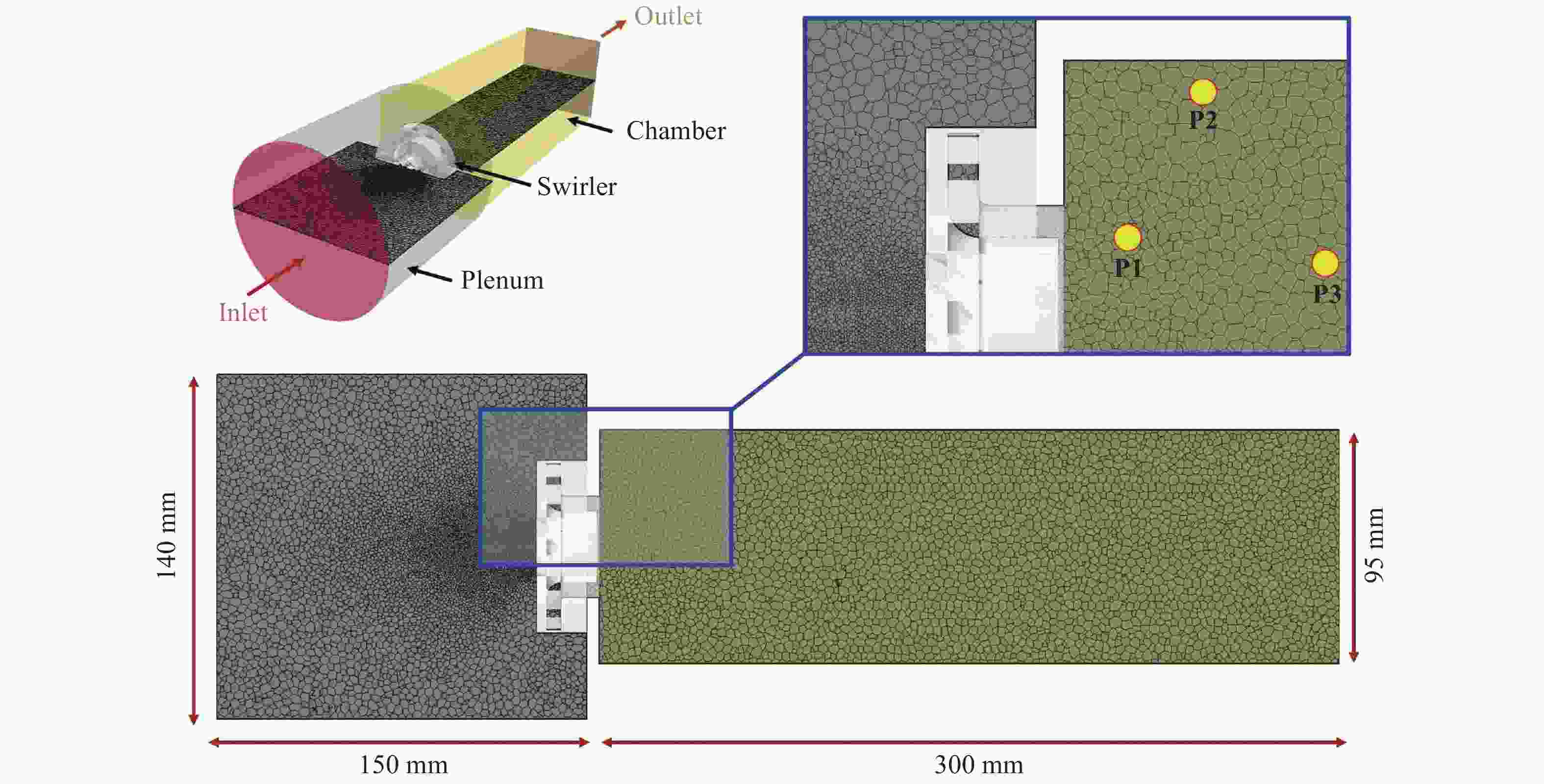
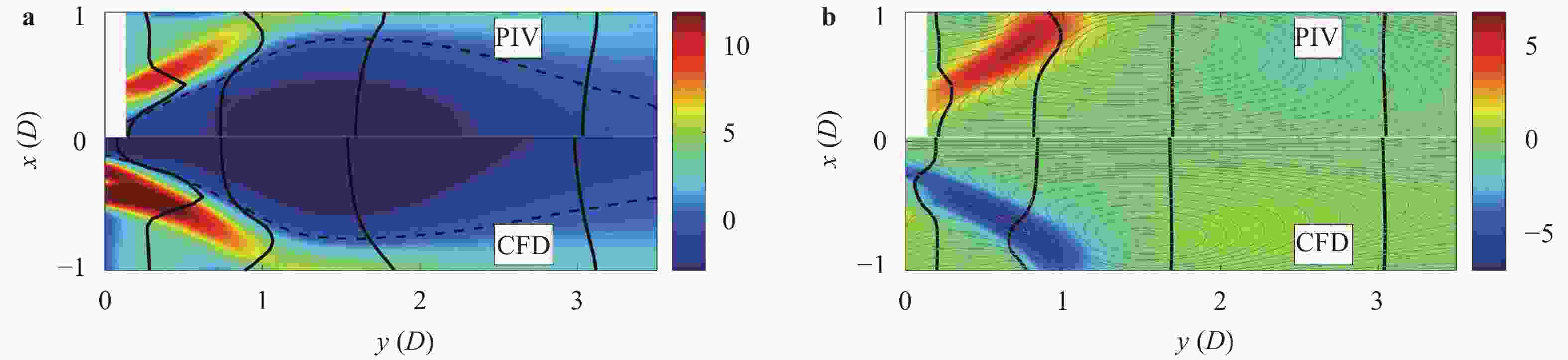
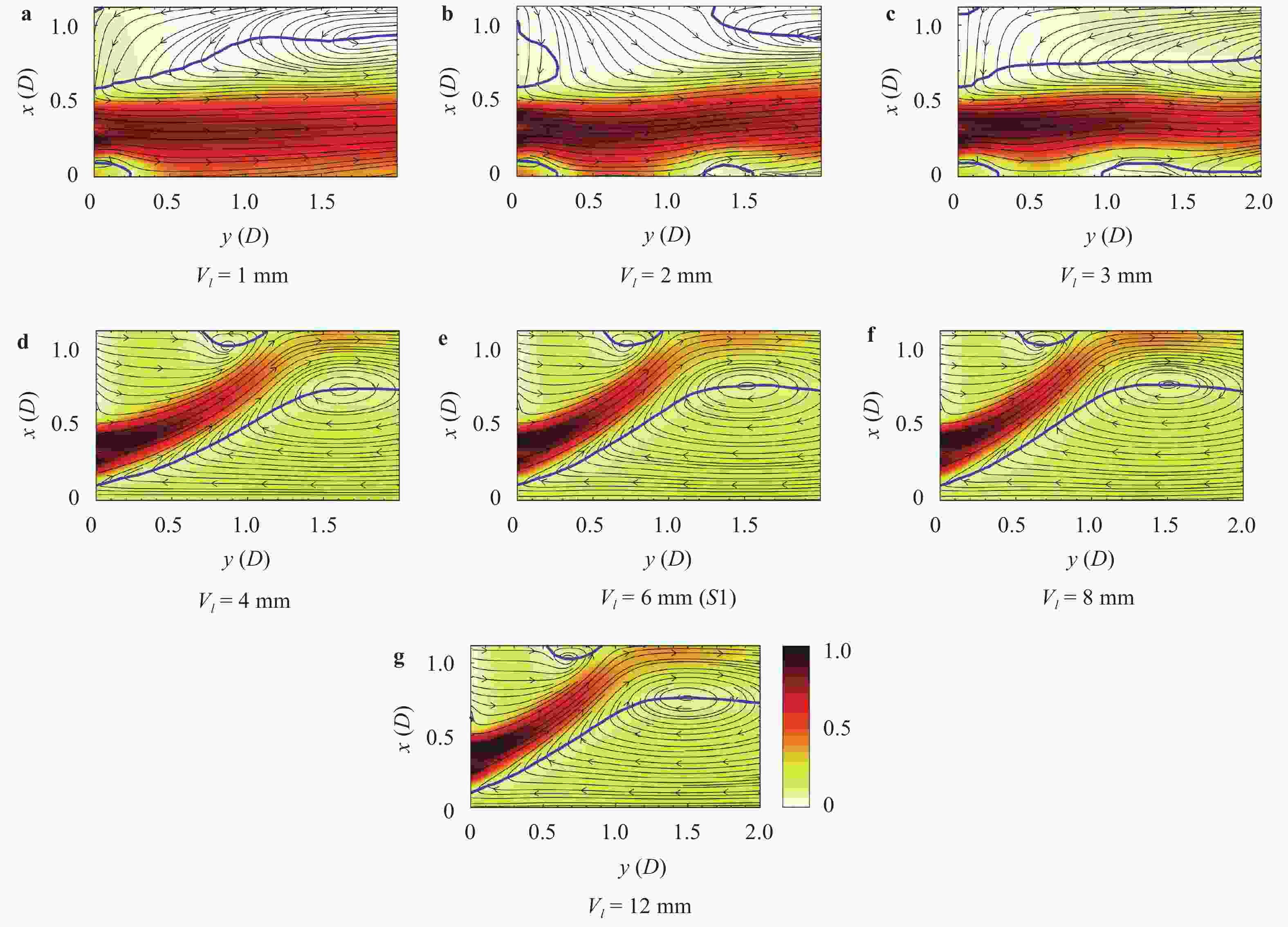
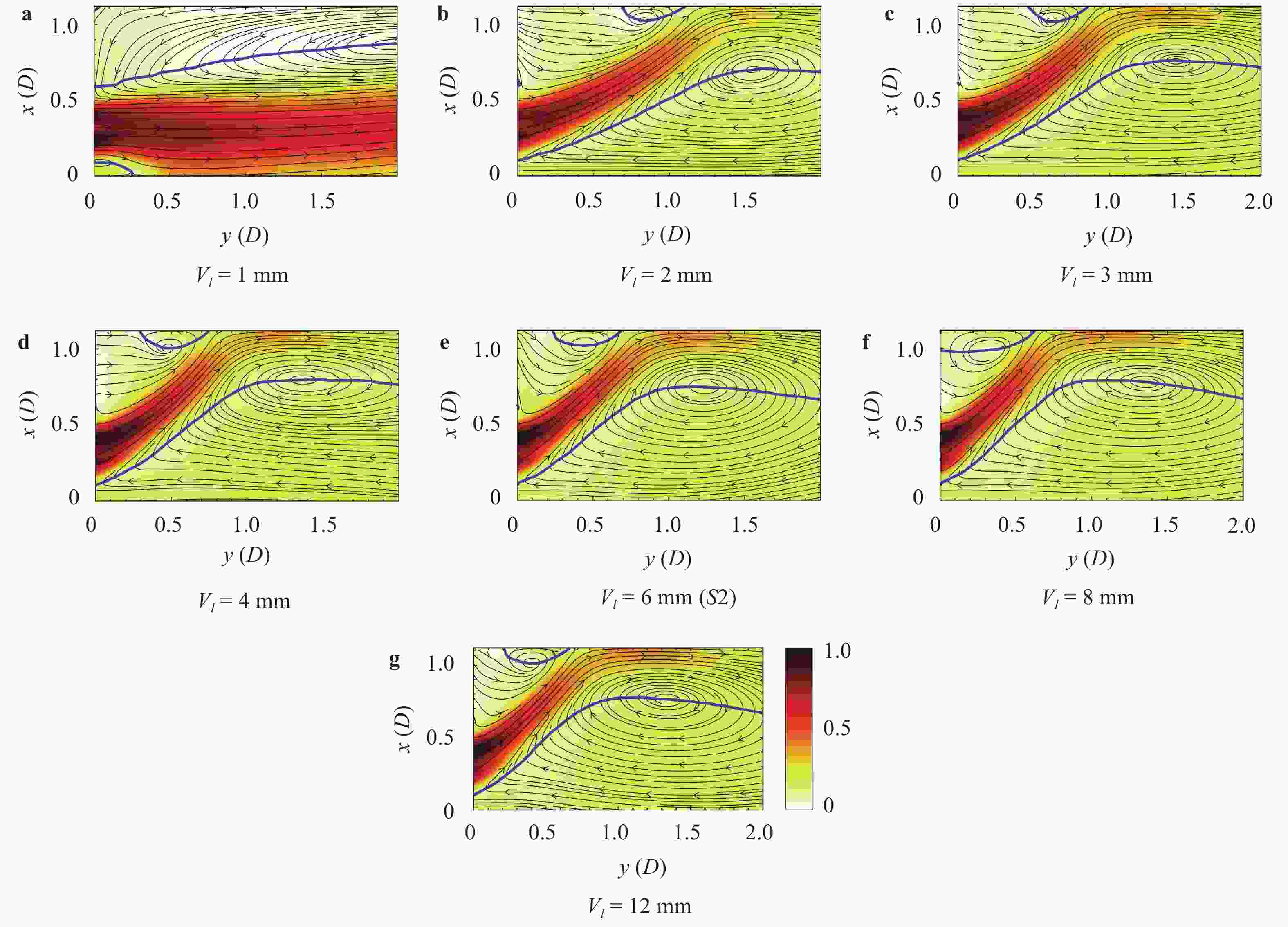
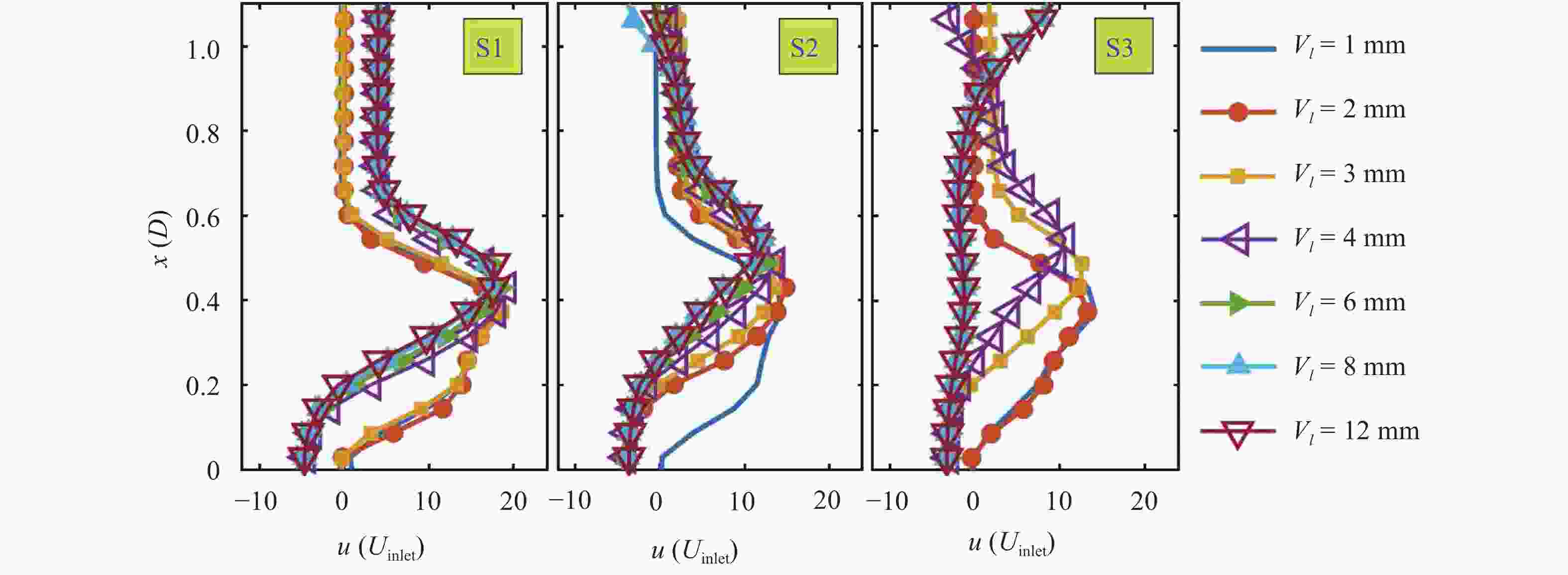
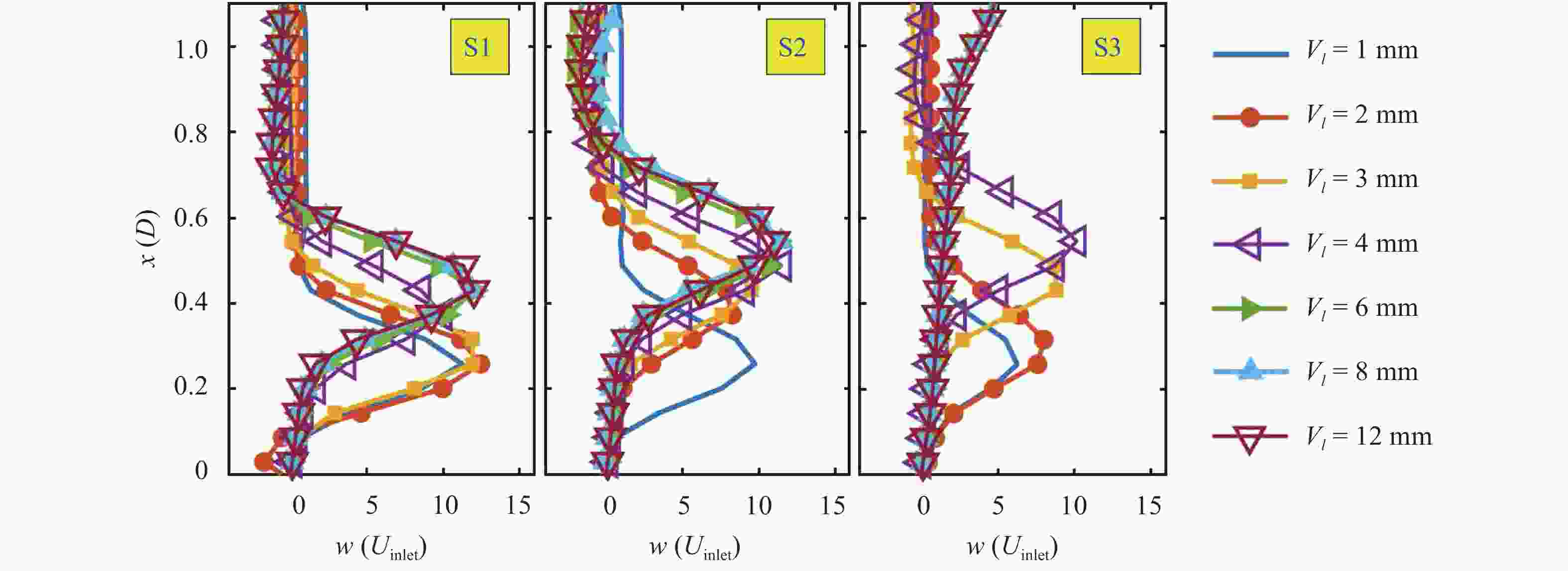
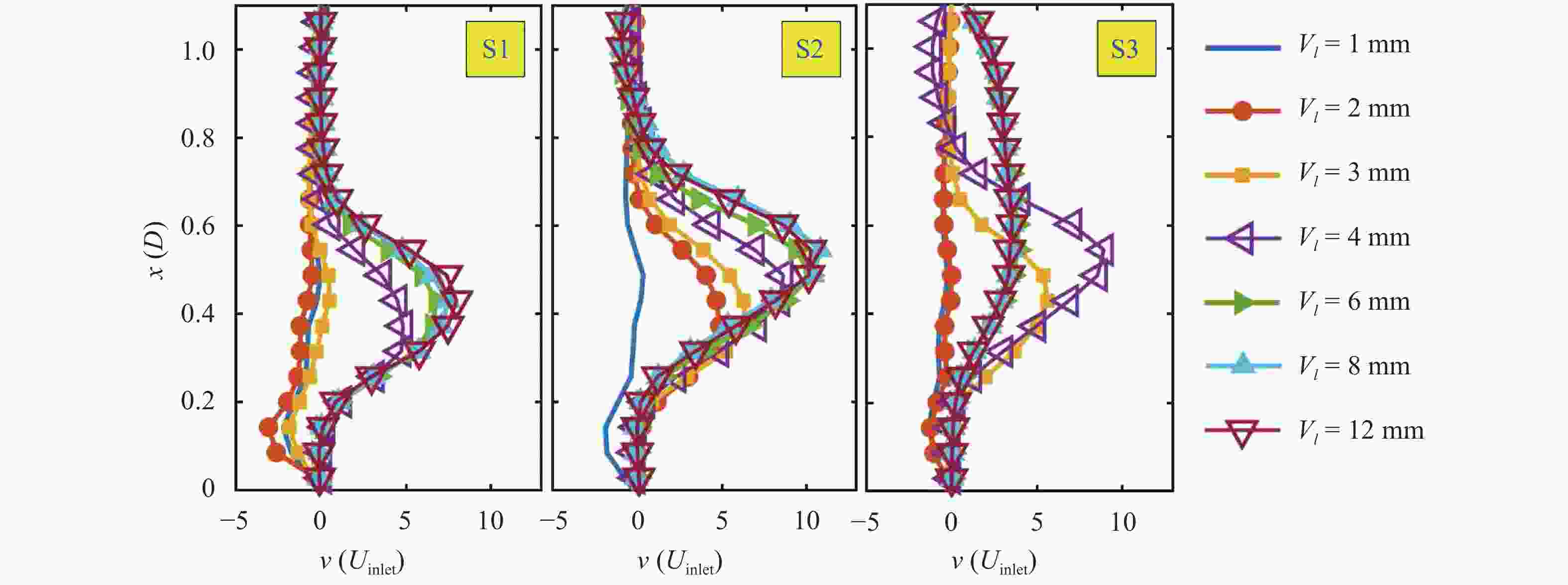
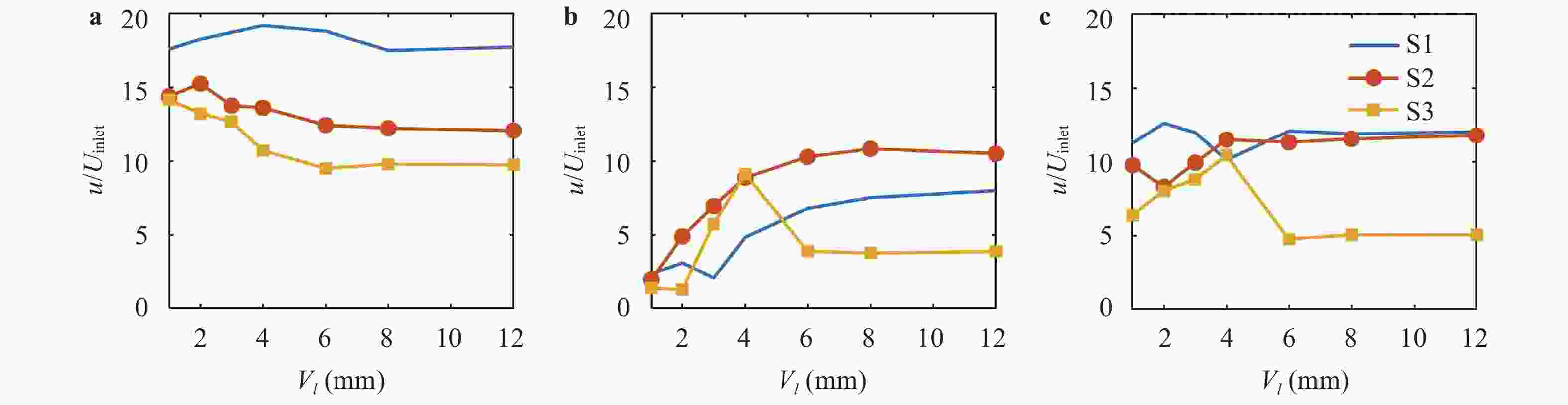
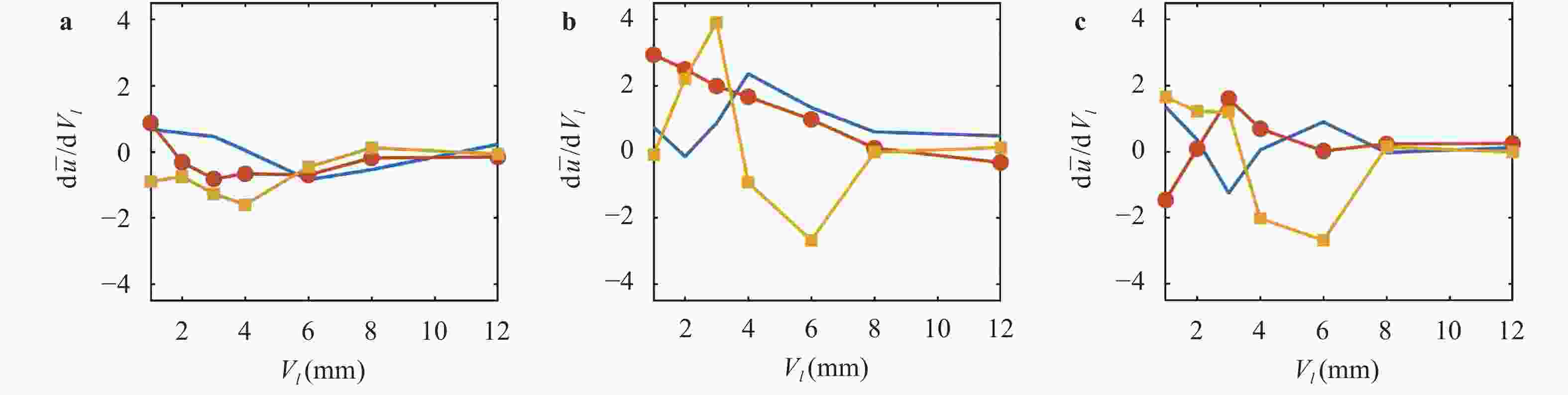
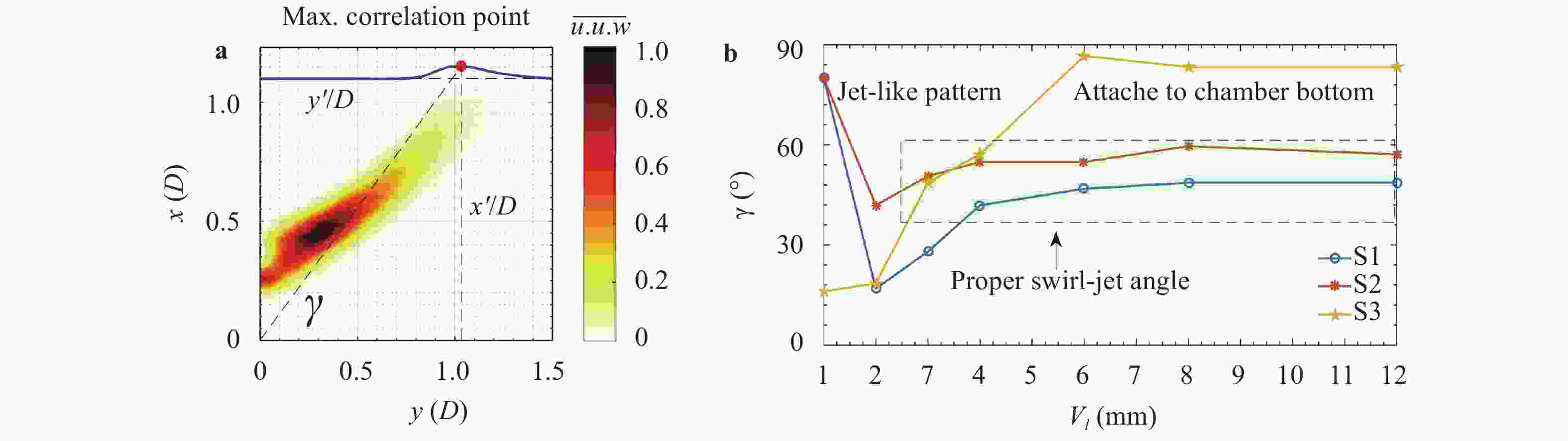
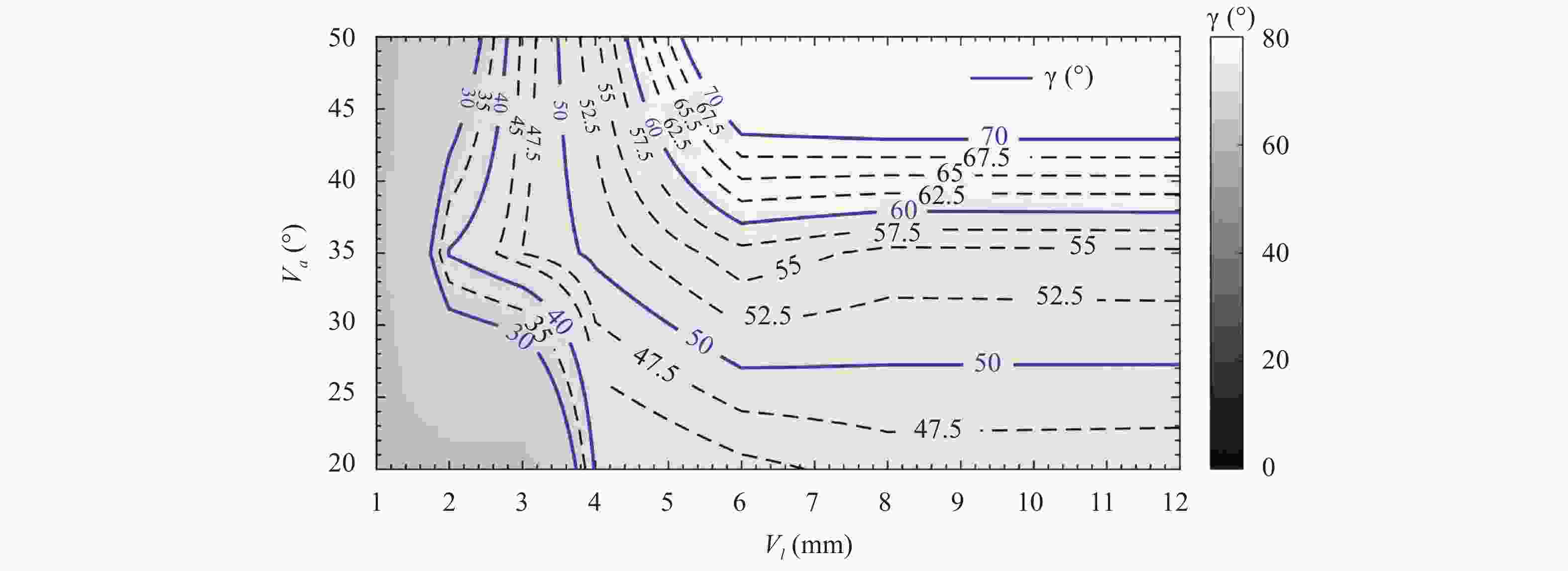
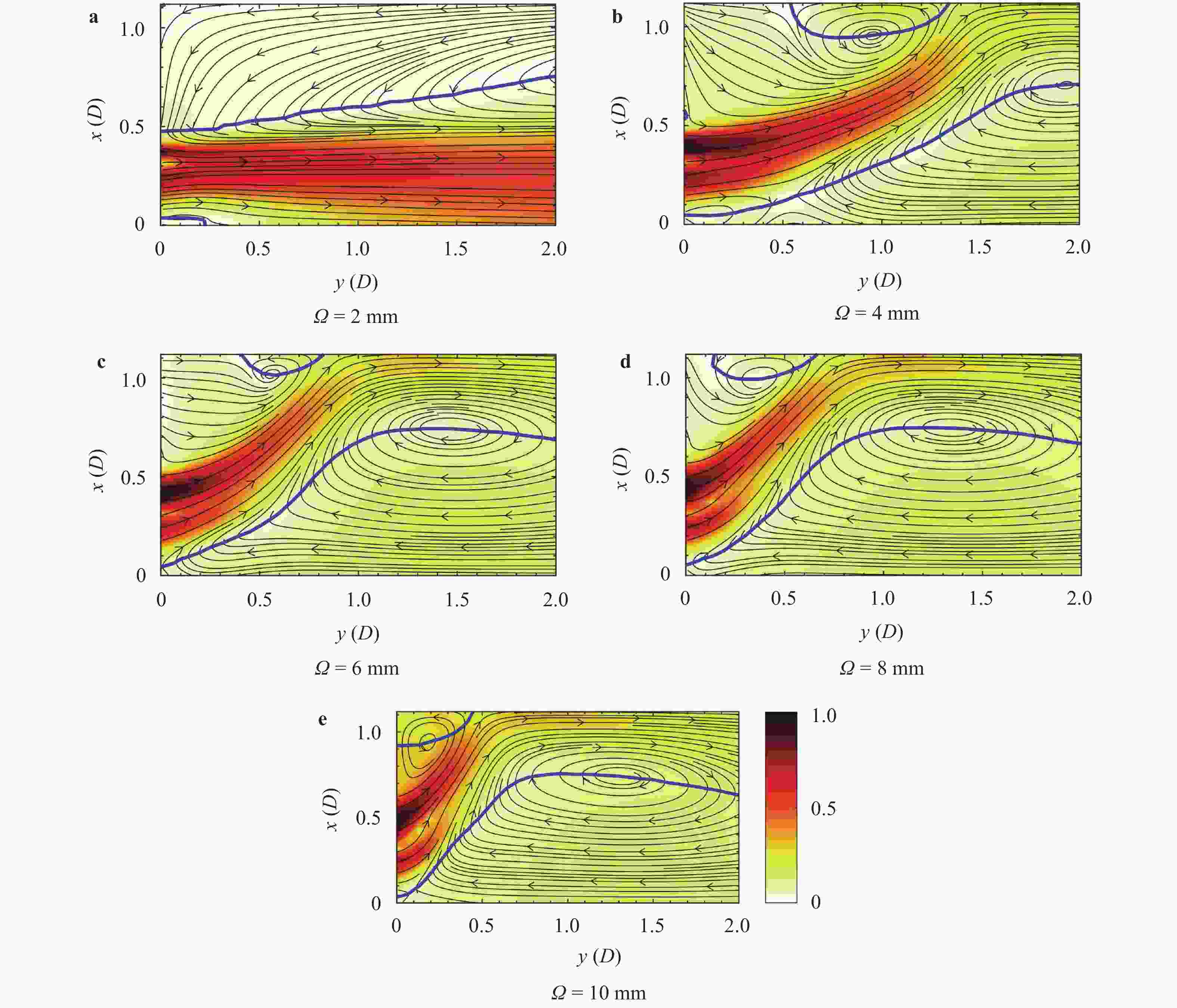
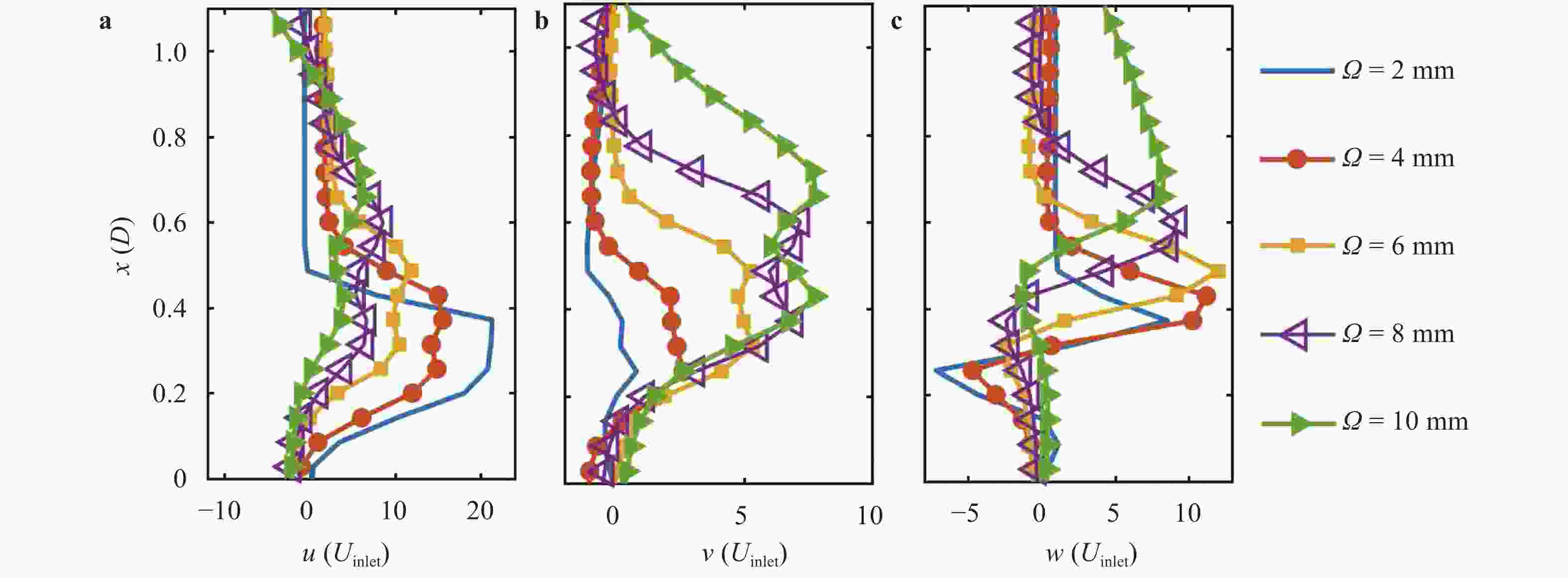
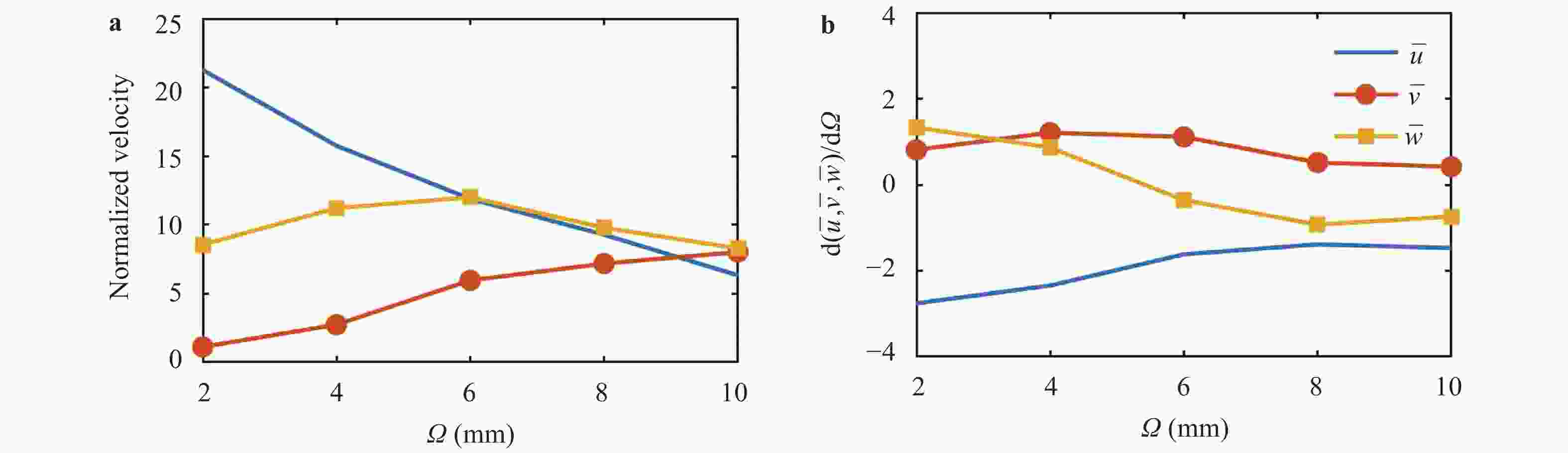
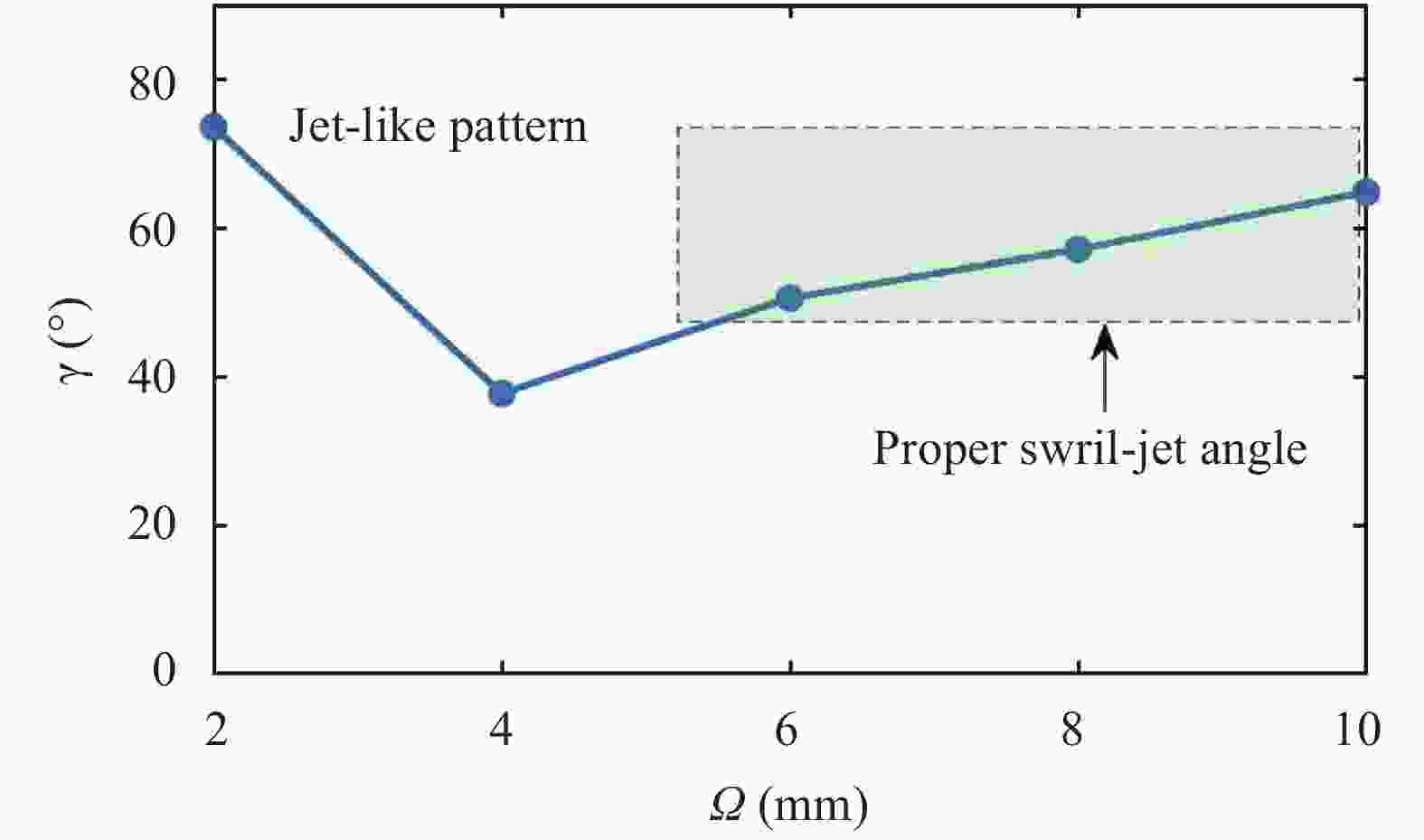
The design of axial or radial swirlers typically governs a number of geometrical parameters that are determined by the desired flow field. In the meantime, the number of unknown parameters increases with the number of concentrically mounted swirlers. The available literature is nonetheless limited, and designers are obligated to increase the number of initial assumptions. In this article, three kinds of triple swirlers are employed and simulations are performed to determine the effect of each parameter on the swirler performance. Based on the correlation provided, over-lengthening the radial vane length could result in significant changes in the flow field from the jet-like pattern to a wide swirl-jet angle due to the Coanda effect. Passage width should also have the potential to alter the swirl-jet angle and velocity field at the exit of the swirler.
The design of axial or radial swirlers typically governs a number of geometrical parameters that are determined by the desired flow field. In the meantime, the number of unknown parameters increases with the number of concentrically mounted swirlers. The available literature is nonetheless limited, and designers are obligated to increase the number of initial assumptions. In this article, three kinds of triple swirlers are employed and simulations are performed to determine the effect of each parameter on the swirler performance. Based on the correlation provided, over-lengthening the radial vane length could result in significant changes in the flow field from the jet-like pattern to a wide swirl-jet angle due to the Coanda effect. Passage width should also have the potential to alter the swirl-jet angle and velocity field at the exit of the swirler.
Theoretical and Applied Mechanics Letters 2019, 9(6): 353-357.
doi: 10.1016/j.taml.2019.06.004
Abstract:
The theory of time scales, which unifies continuous and discrete analysis, provides a powerful mathematical tool for the study of complex dynamic systems. It enables us to understand more clearly the essential problems of continuous systems and discrete systems as well as other complex systems. In this paper, the theory of generalized canonical transformation for second-order Birkhoffian systems on time scales is proposed and studied, which extends the canonical transformation theory of Hamilton canonical equations. First, the condition of generalized canonical transformation for the second-order Birkhoffian system on time scales is established. Second, based on this condition, six basic forms of generalized canonical transformation for the second-order Birkhoffian system on time scales are given. Also, the relationships between new variables and old variables for each of these cases are derived. In the end, an example is given to show the application of the results.
The theory of time scales, which unifies continuous and discrete analysis, provides a powerful mathematical tool for the study of complex dynamic systems. It enables us to understand more clearly the essential problems of continuous systems and discrete systems as well as other complex systems. In this paper, the theory of generalized canonical transformation for second-order Birkhoffian systems on time scales is proposed and studied, which extends the canonical transformation theory of Hamilton canonical equations. First, the condition of generalized canonical transformation for the second-order Birkhoffian system on time scales is established. Second, based on this condition, six basic forms of generalized canonical transformation for the second-order Birkhoffian system on time scales are given. Also, the relationships between new variables and old variables for each of these cases are derived. In the end, an example is given to show the application of the results.
Theoretical and Applied Mechanics Letters 2019, 9(6): 358-362.
doi: 10.1016/j.taml.2019.05.010
Abstract:
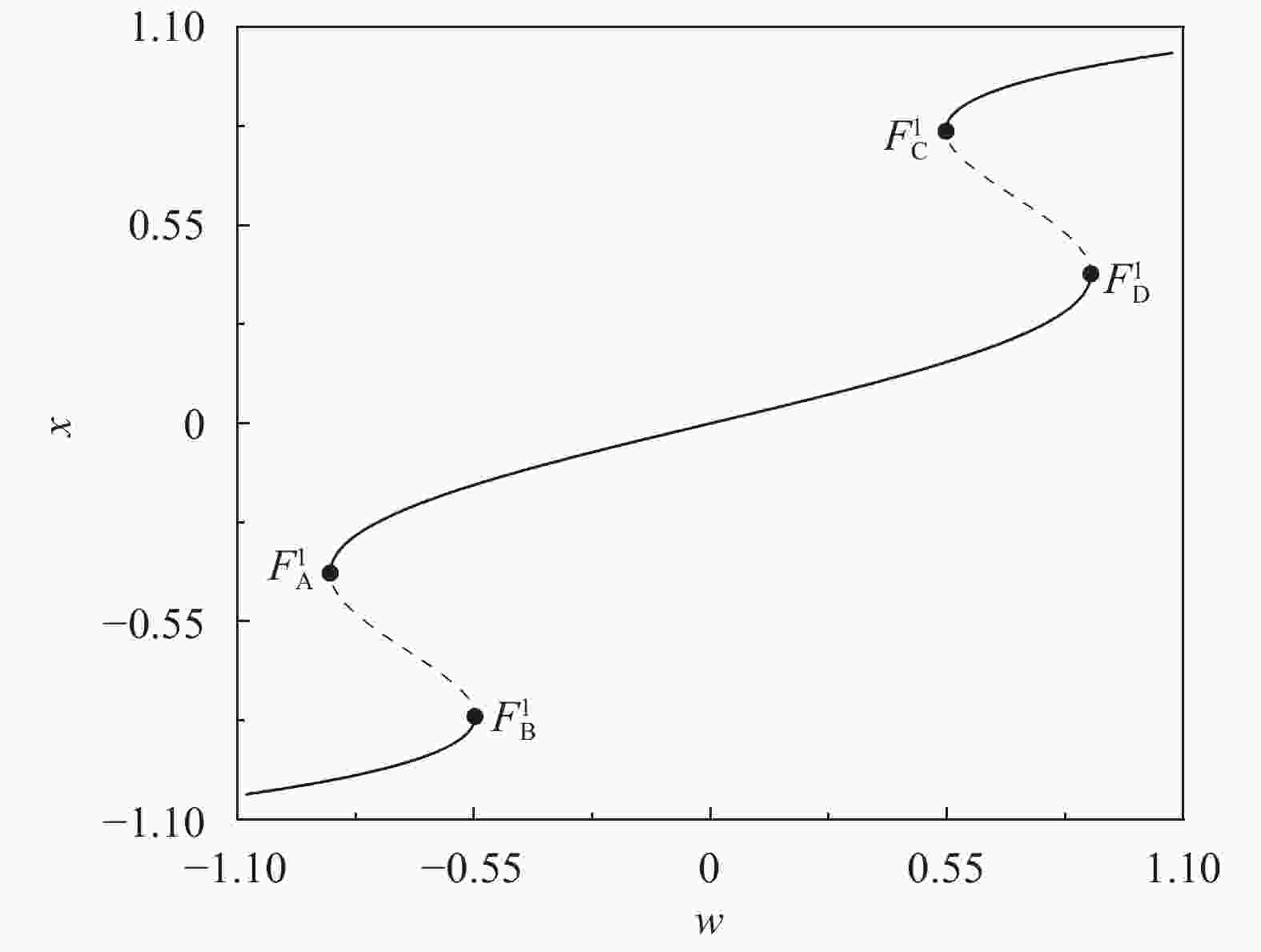
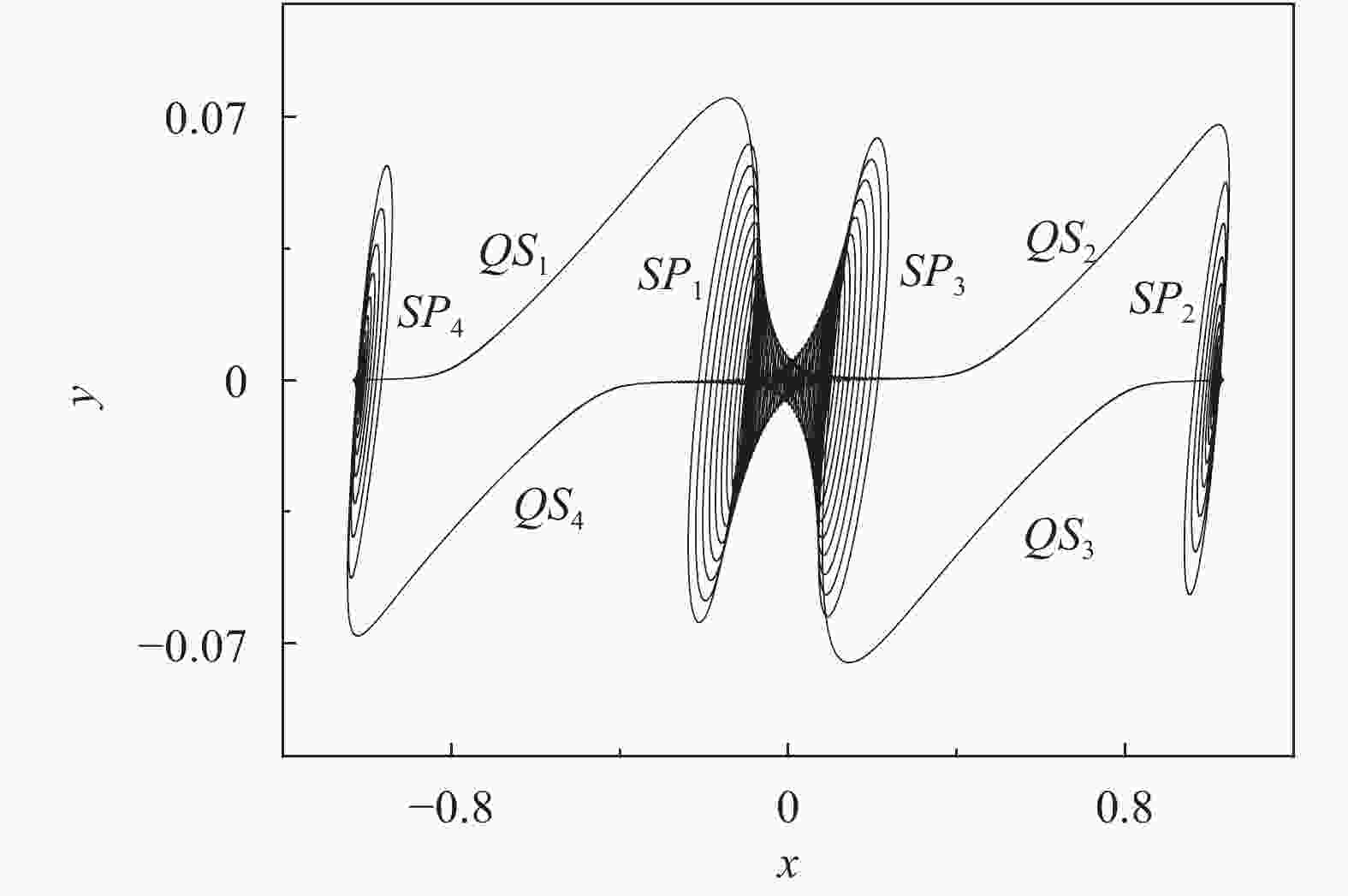
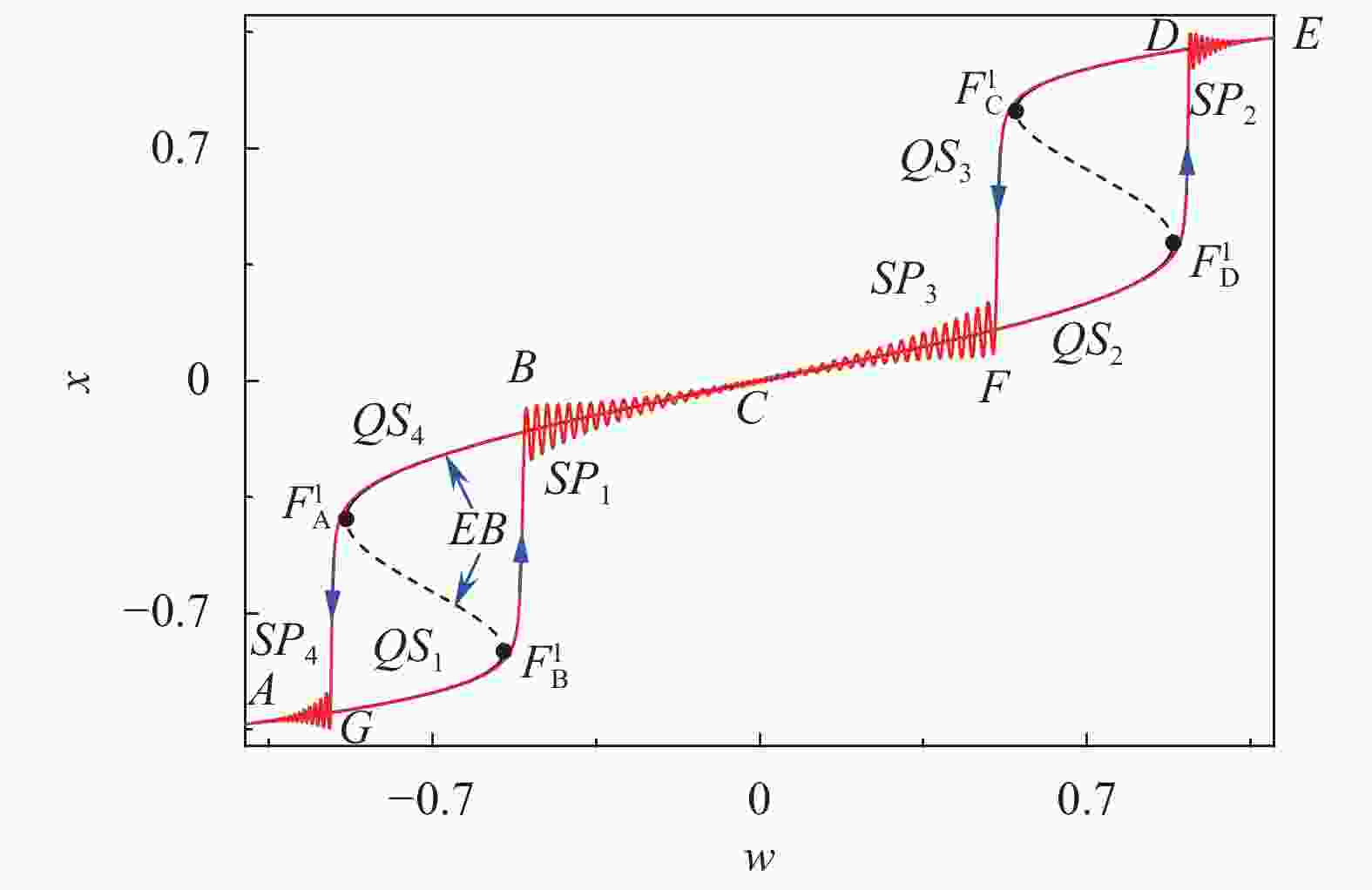
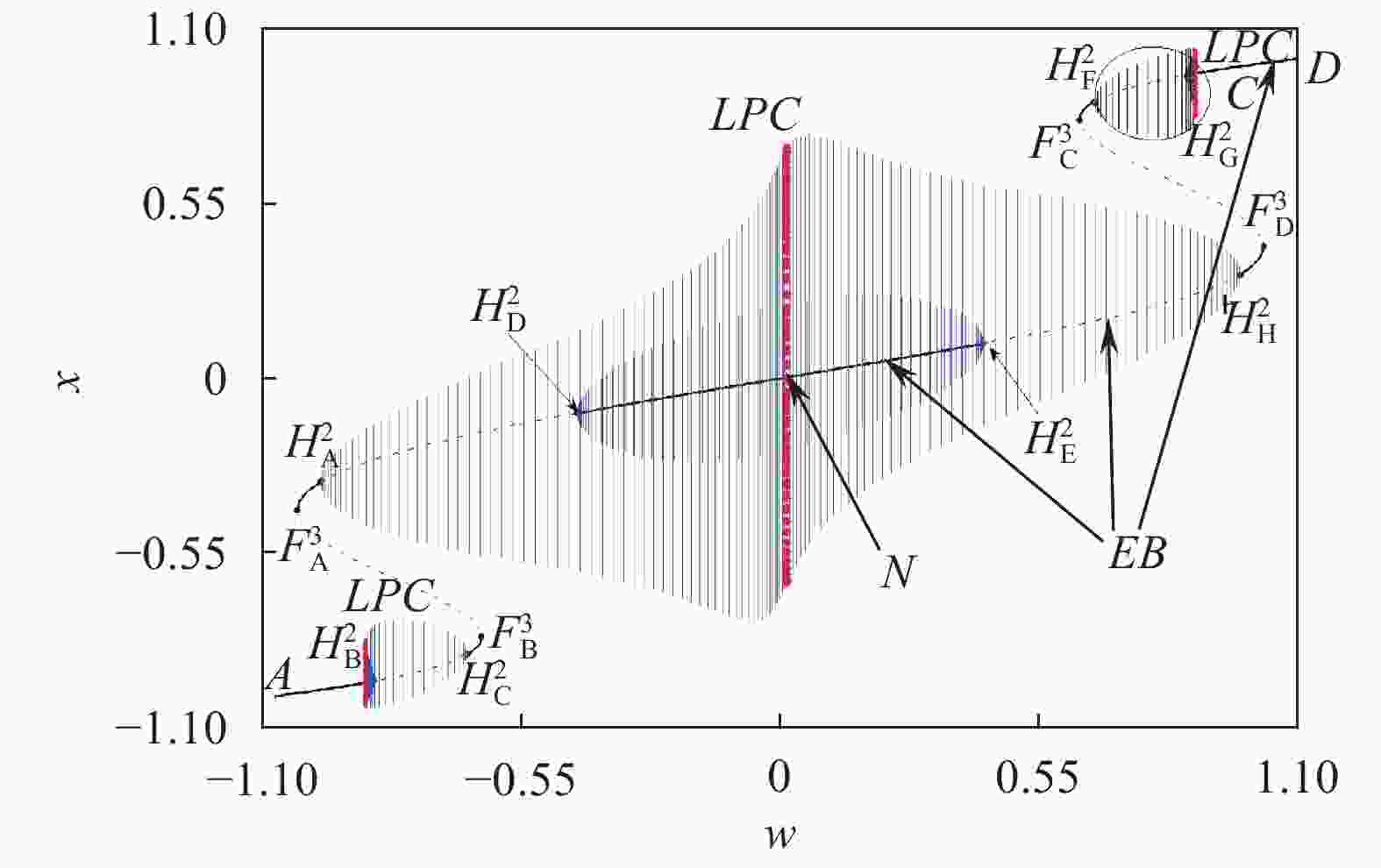
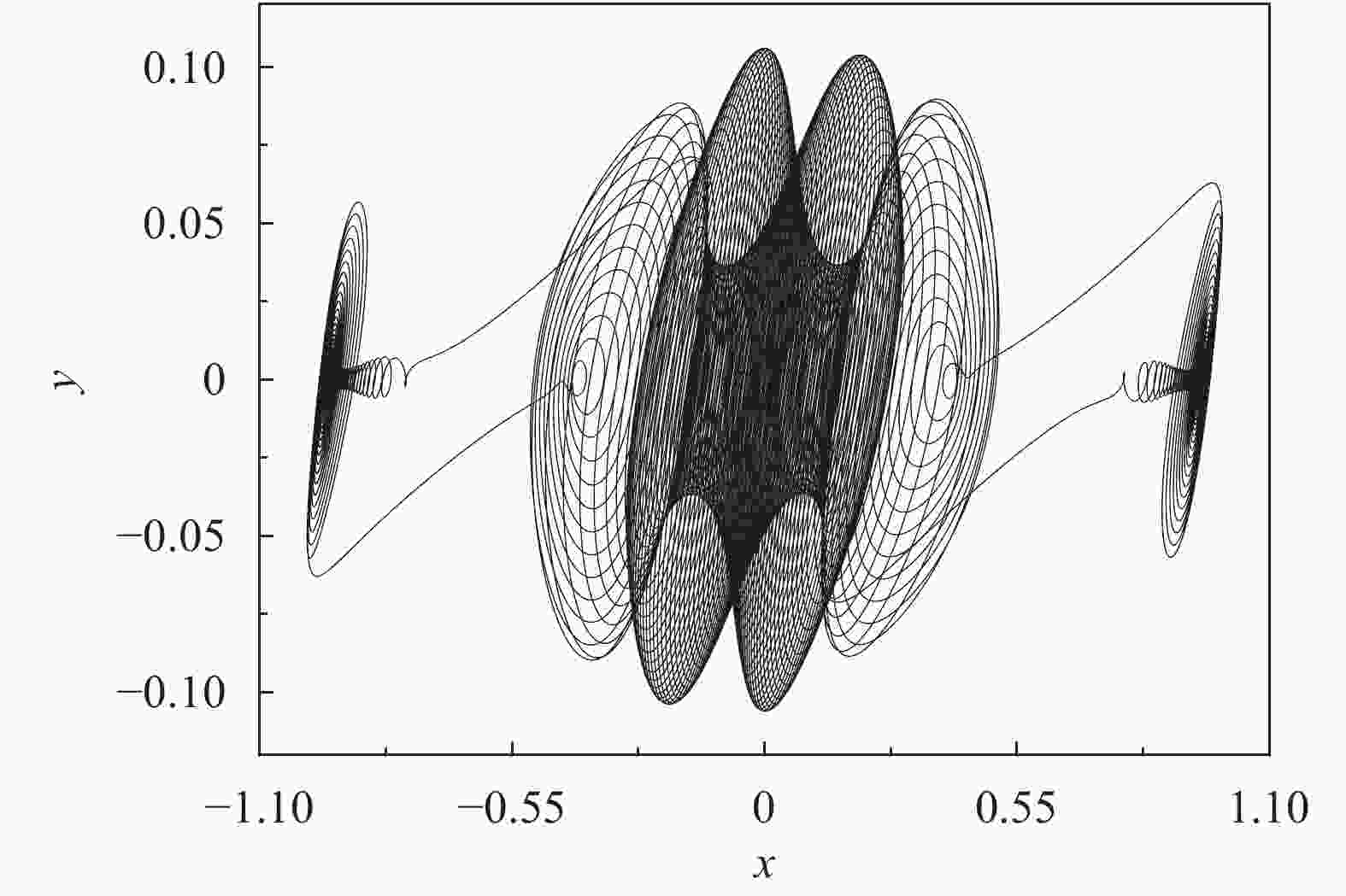
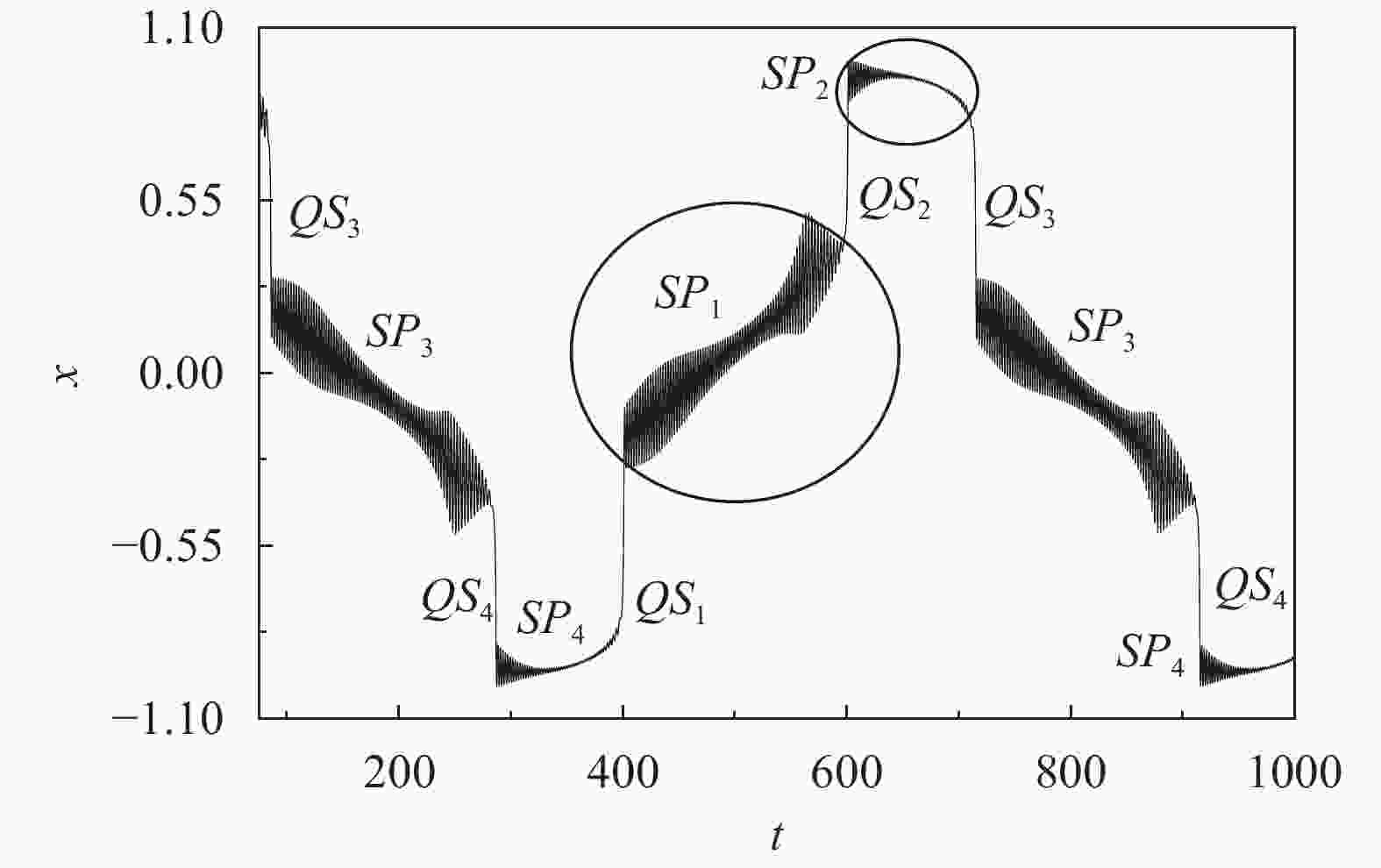
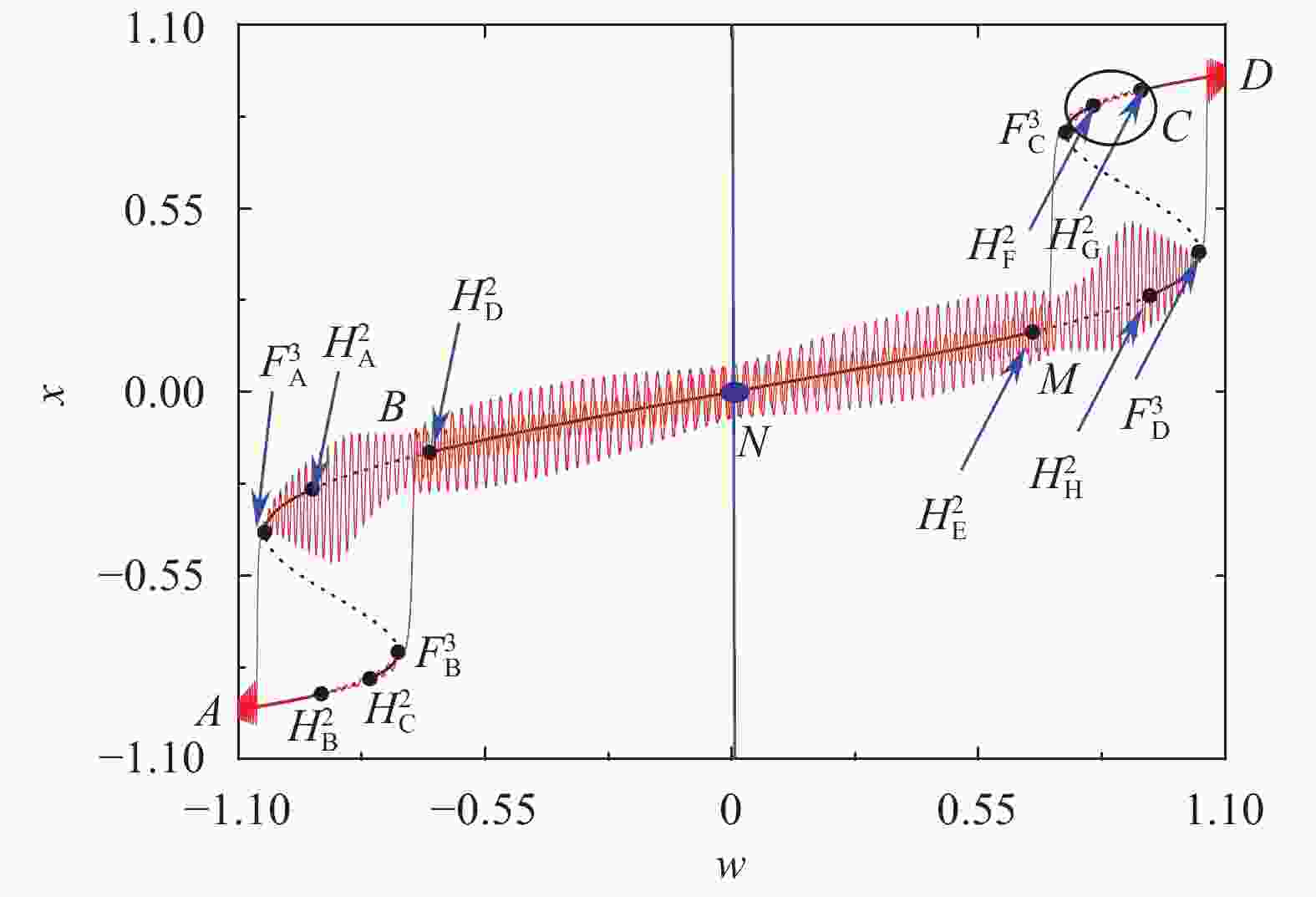
A modified slow-fast analysis method is presented for the periodically excited non-autonomous dynamical system with an order gap between the exciting frequency and the natural frequency. By regarding the exciting term as a slow-varying parameter, a generalized autonomous fast subsystem can be defined, the equilibrium branches as well as the bifurcations of which can be employed to account for the mechanism of the bursting oscillations by combining the transformed phase portrait introduced. As an example, a typical periodically excited Hartley model is used to demonstrate the validness of the method, in which the exciting frequency is far less than the natural frequency. The equilibrium branches and their bifurcations of the fast subsystem with the variation of the slow-varying parameter are presented. Bursting oscillations for two typical cases are considered, which reveals that, fold bifurcation may cause the the trajectory to jump between different equilibrium branches, while Hopf bifurcation may cause the trajectory to oscillate around the stable limit cycle.
A modified slow-fast analysis method is presented for the periodically excited non-autonomous dynamical system with an order gap between the exciting frequency and the natural frequency. By regarding the exciting term as a slow-varying parameter, a generalized autonomous fast subsystem can be defined, the equilibrium branches as well as the bifurcations of which can be employed to account for the mechanism of the bursting oscillations by combining the transformed phase portrait introduced. As an example, a typical periodically excited Hartley model is used to demonstrate the validness of the method, in which the exciting frequency is far less than the natural frequency. The equilibrium branches and their bifurcations of the fast subsystem with the variation of the slow-varying parameter are presented. Bursting oscillations for two typical cases are considered, which reveals that, fold bifurcation may cause the the trajectory to jump between different equilibrium branches, while Hopf bifurcation may cause the trajectory to oscillate around the stable limit cycle.
Theoretical and Applied Mechanics Letters 2019, 9(6): 376-381.
doi: 10.1016/j.taml.2019.05.006
Abstract:
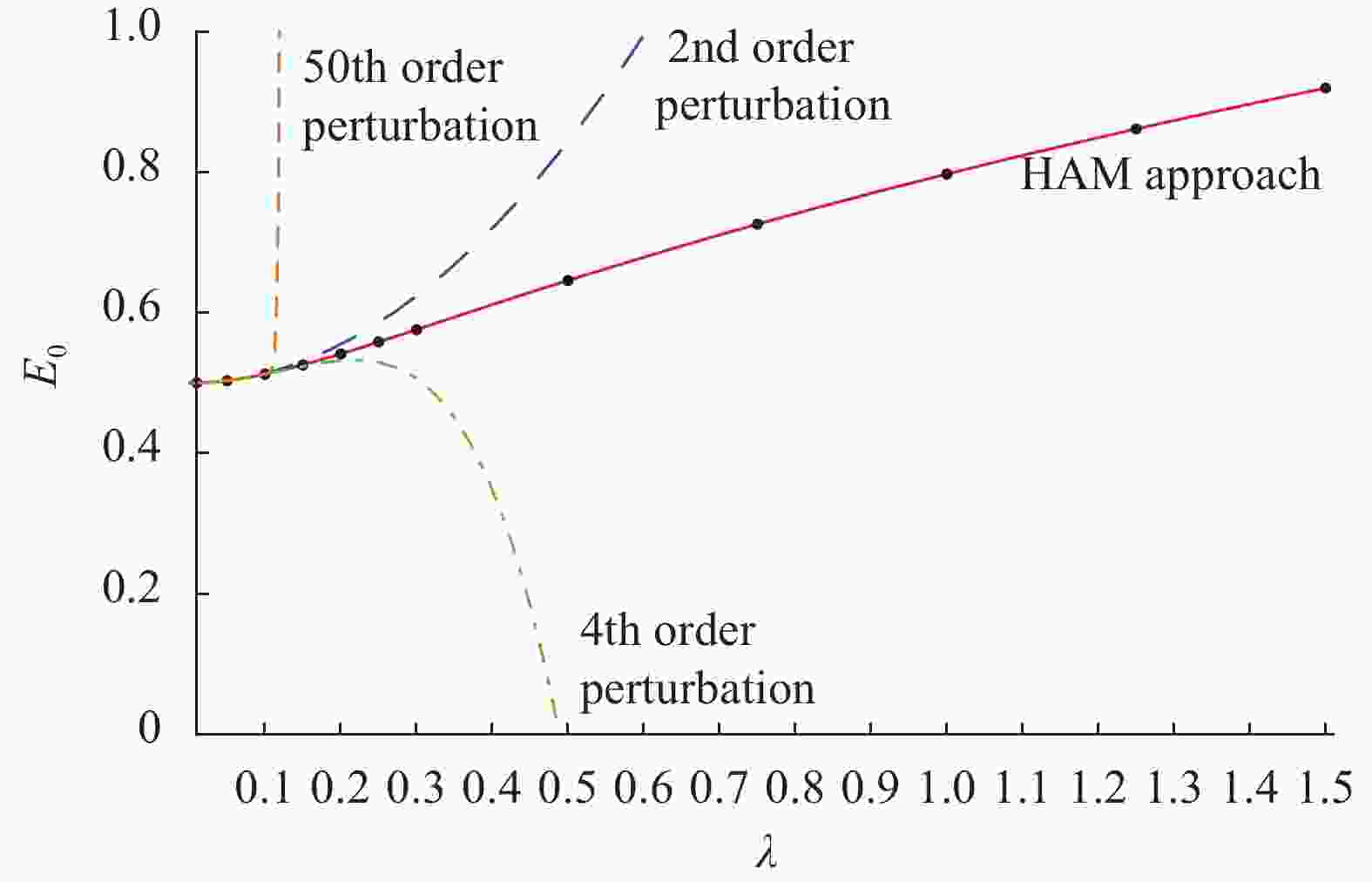
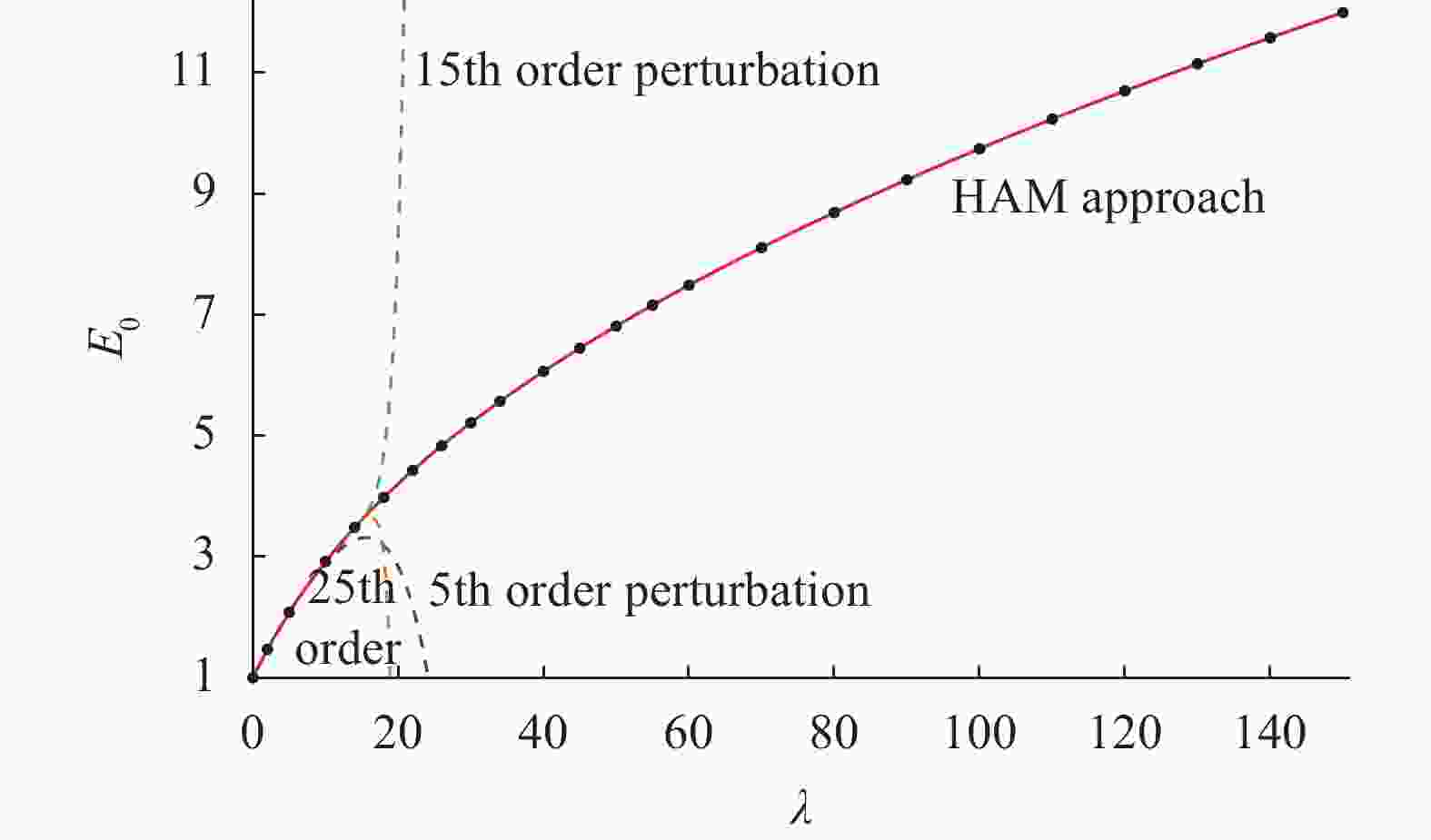
A general analytic approach, namely the homotopy analysis method (HAM), is applied to solve the time independent Schrödinger equations. Unlike perturbation method, the HAM-based approach does not depend on any small physical parameters, corresponding to small disturbances. Especially, it provides a convenient way to gain the convergent series solution of quantum mechanics. This study illustrates the advantages of this HAM-based approach over the traditional perturbative approach, and its general validity for the Schrödinger equations. Note that perturbation methods are widely used in quantum mechanics, but perturbation results are hardly convergent. This study suggests that the HAM might provide us a new, powerful alternative to gain convergent series solution for some complicated problems in quantum mechanics, including many-body problems, which can be directly compared with the experiment data to improve the accuracy of the experimental findings and/or physical theories.
A general analytic approach, namely the homotopy analysis method (HAM), is applied to solve the time independent Schrödinger equations. Unlike perturbation method, the HAM-based approach does not depend on any small physical parameters, corresponding to small disturbances. Especially, it provides a convenient way to gain the convergent series solution of quantum mechanics. This study illustrates the advantages of this HAM-based approach over the traditional perturbative approach, and its general validity for the Schrödinger equations. Note that perturbation methods are widely used in quantum mechanics, but perturbation results are hardly convergent. This study suggests that the HAM might provide us a new, powerful alternative to gain convergent series solution for some complicated problems in quantum mechanics, including many-body problems, which can be directly compared with the experiment data to improve the accuracy of the experimental findings and/or physical theories.
Theoretical and Applied Mechanics Letters 2019, 9(6): 382-390.
doi: 10.1016/j.taml.2019.05.005
Abstract:
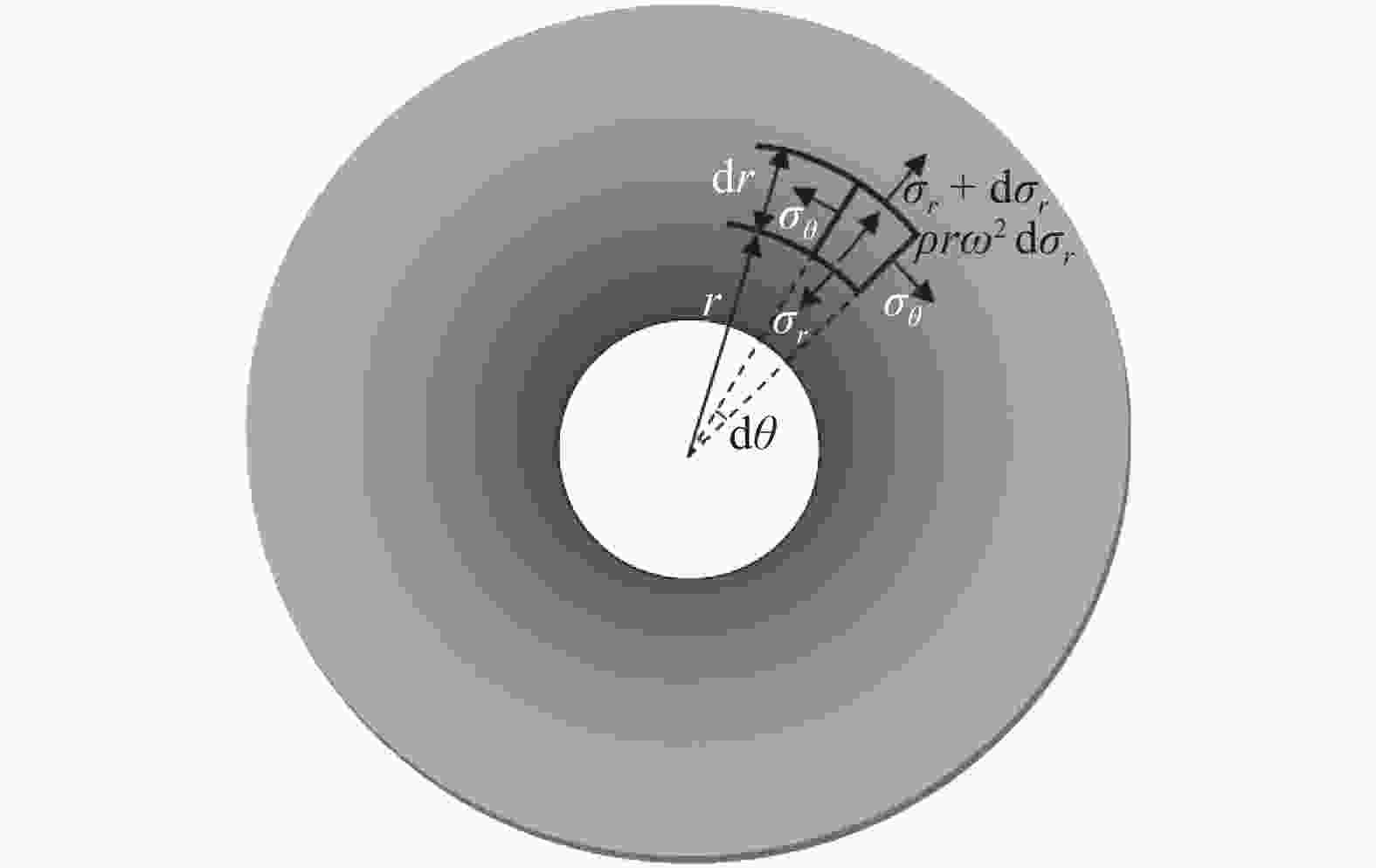
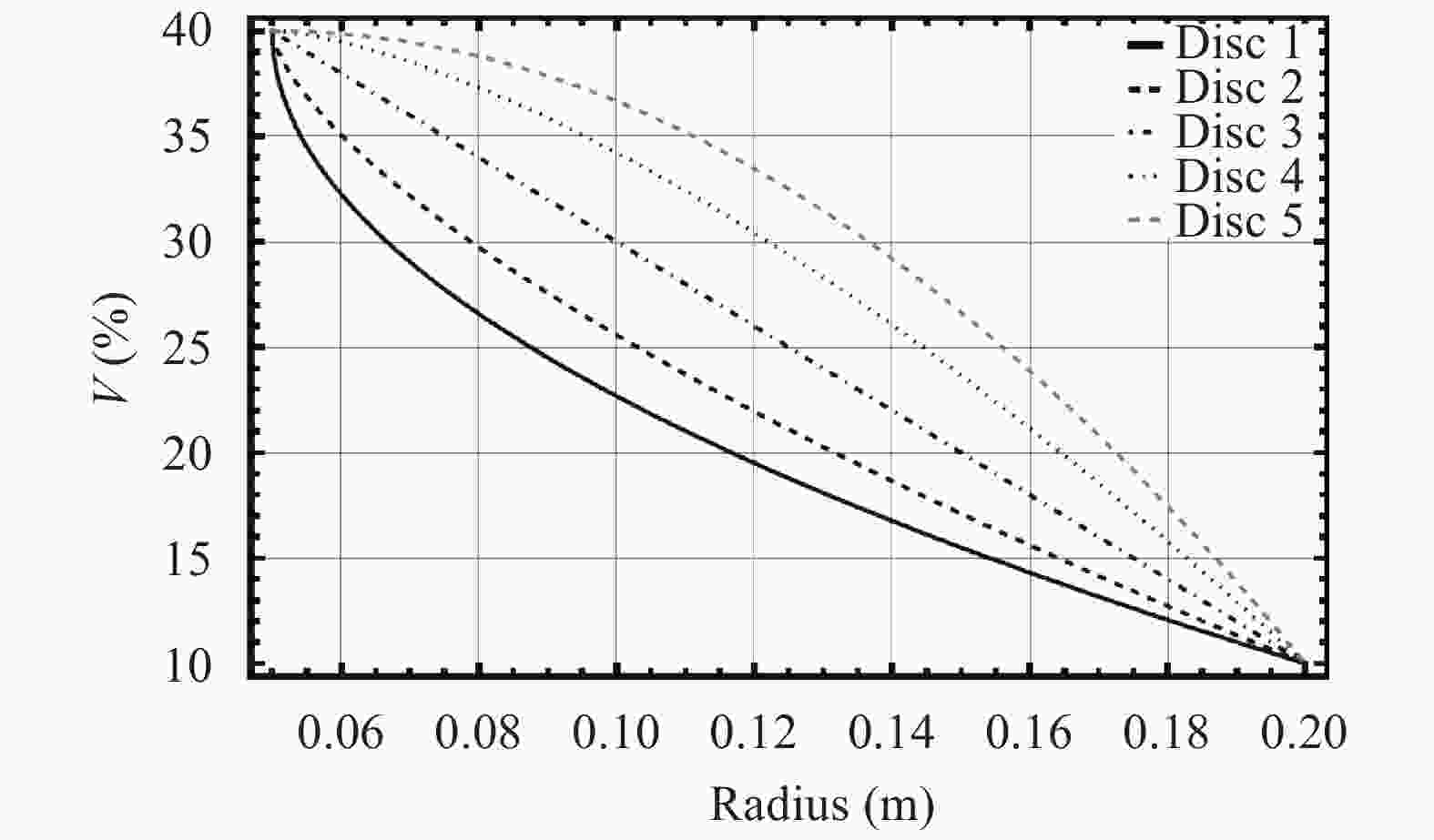
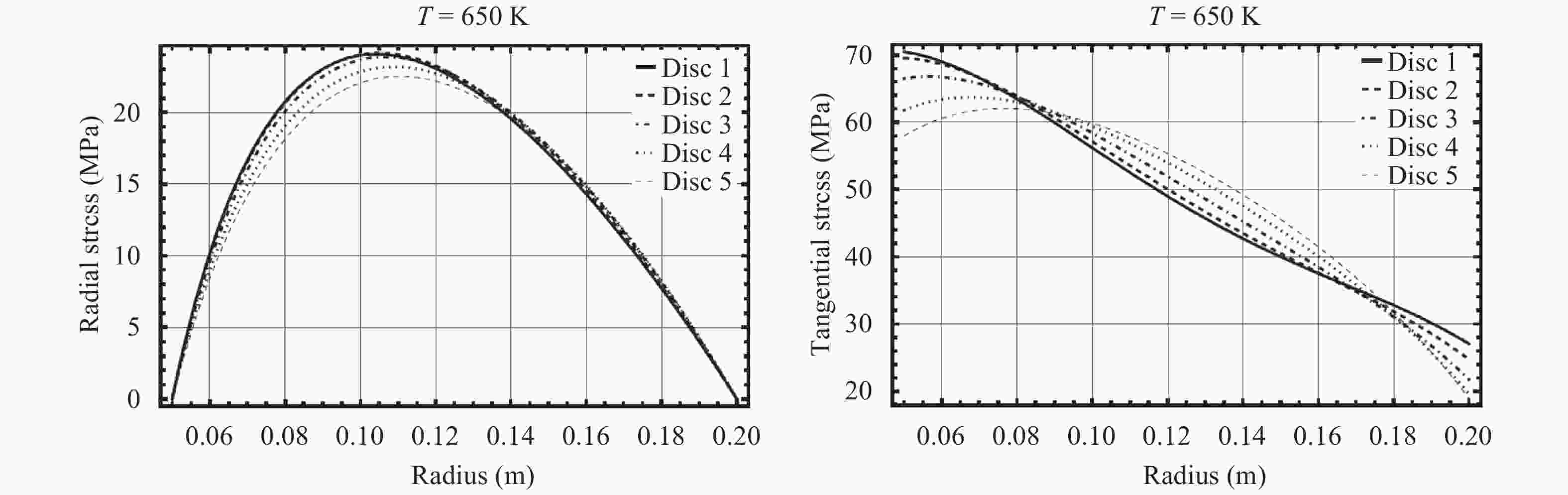
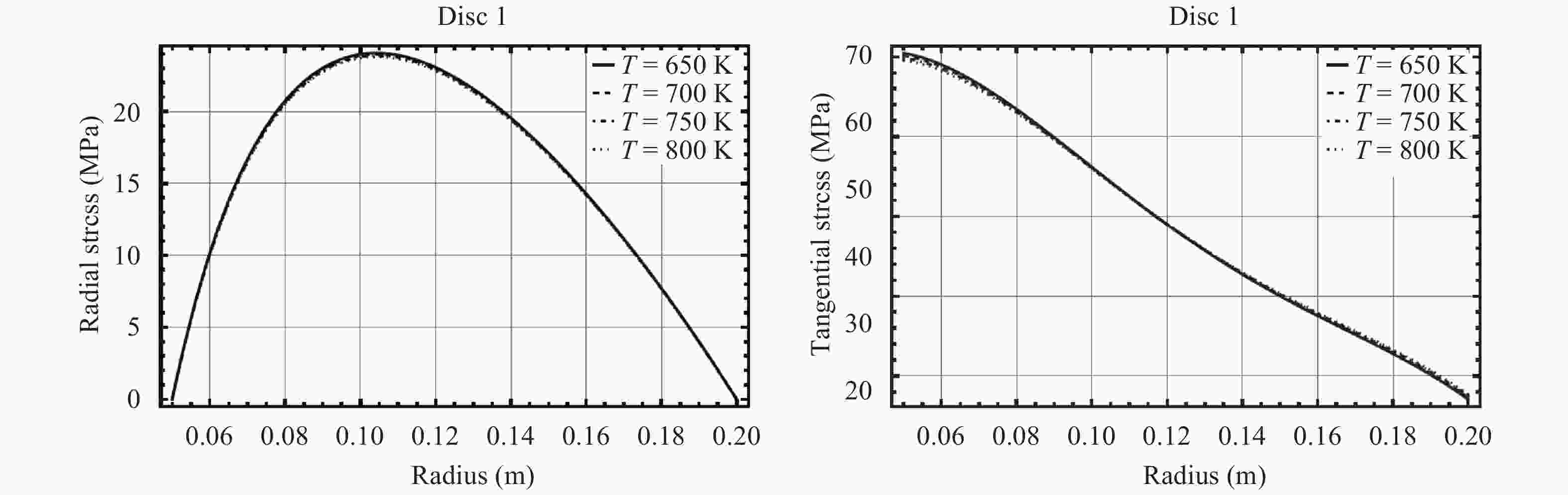
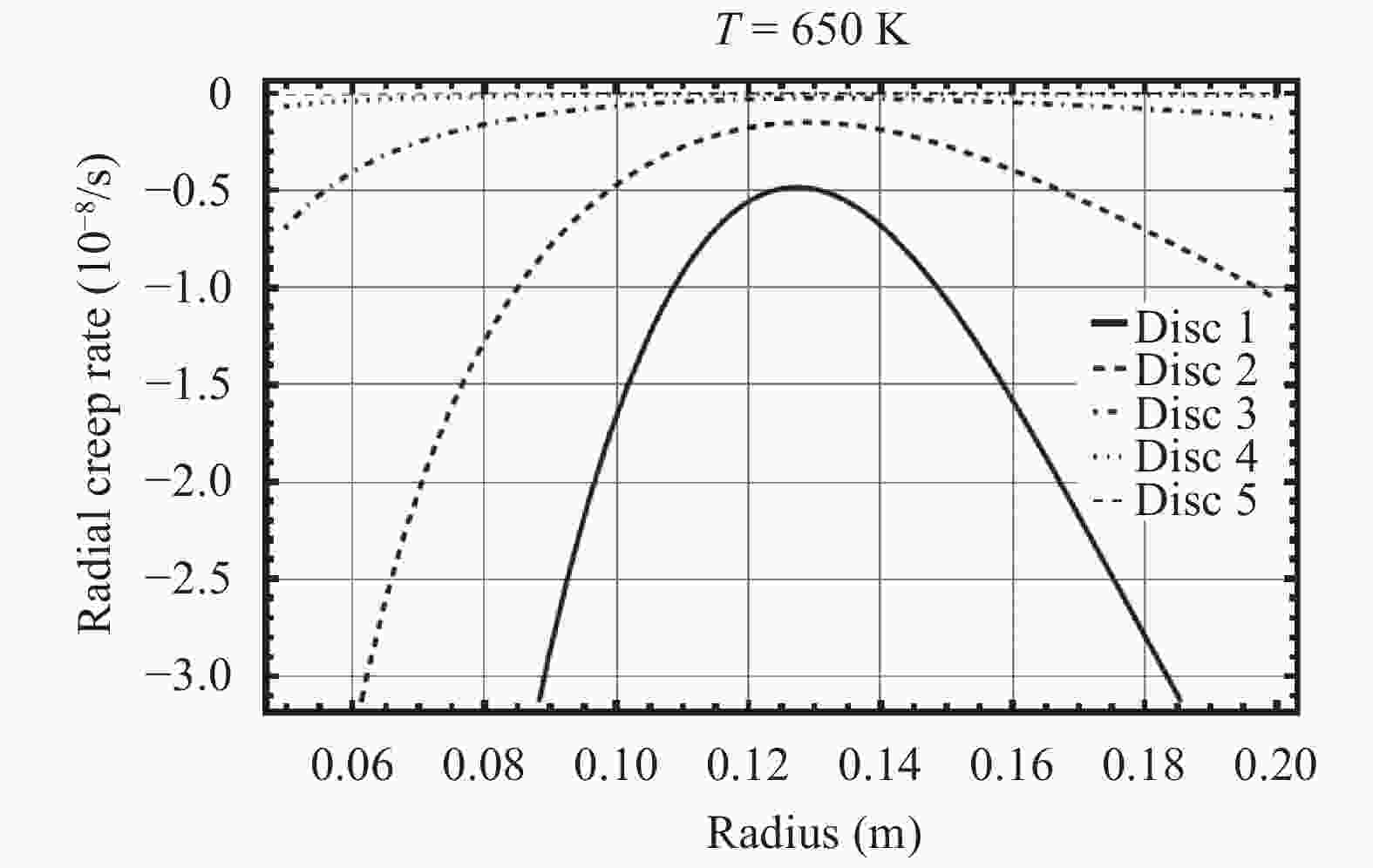
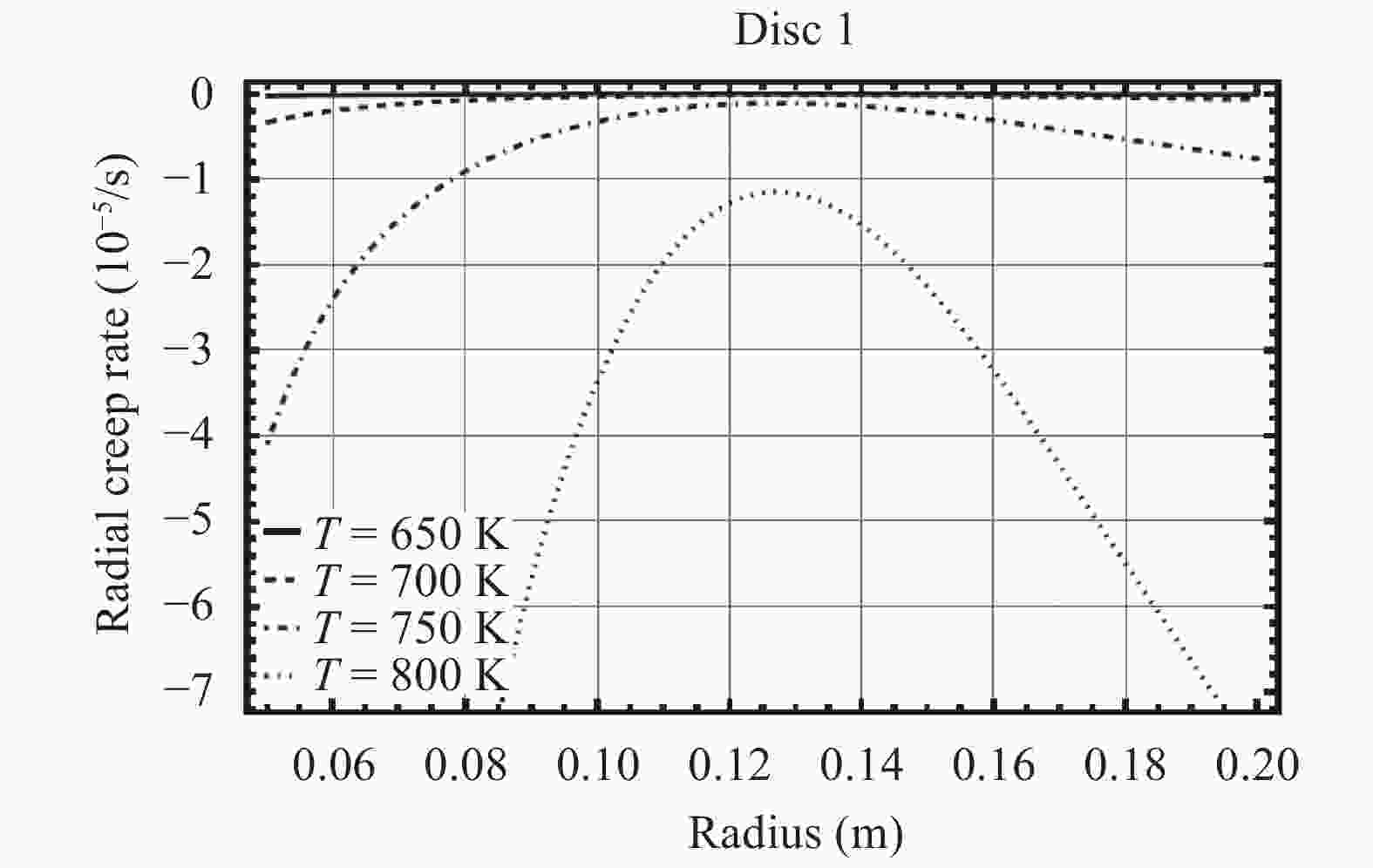
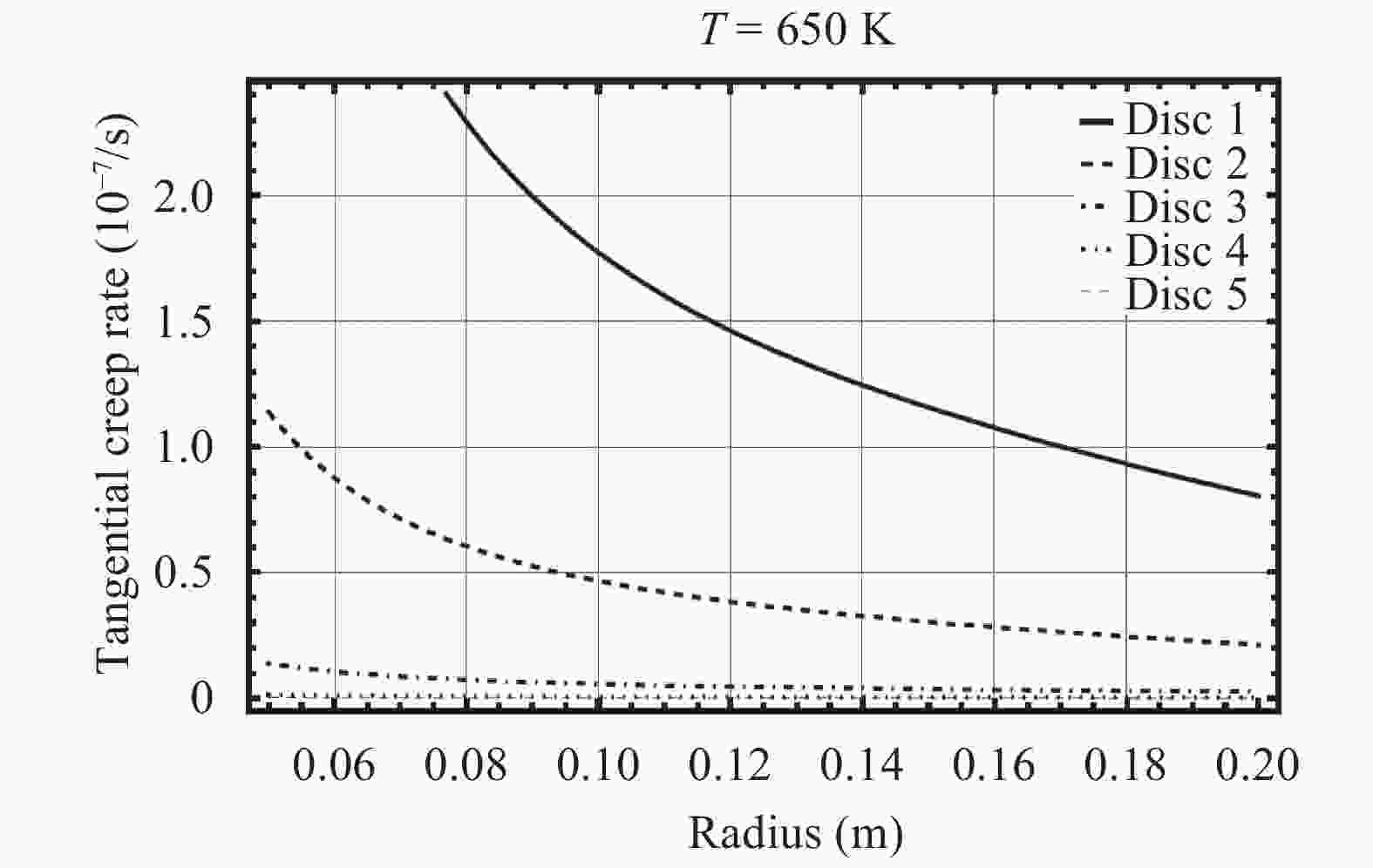
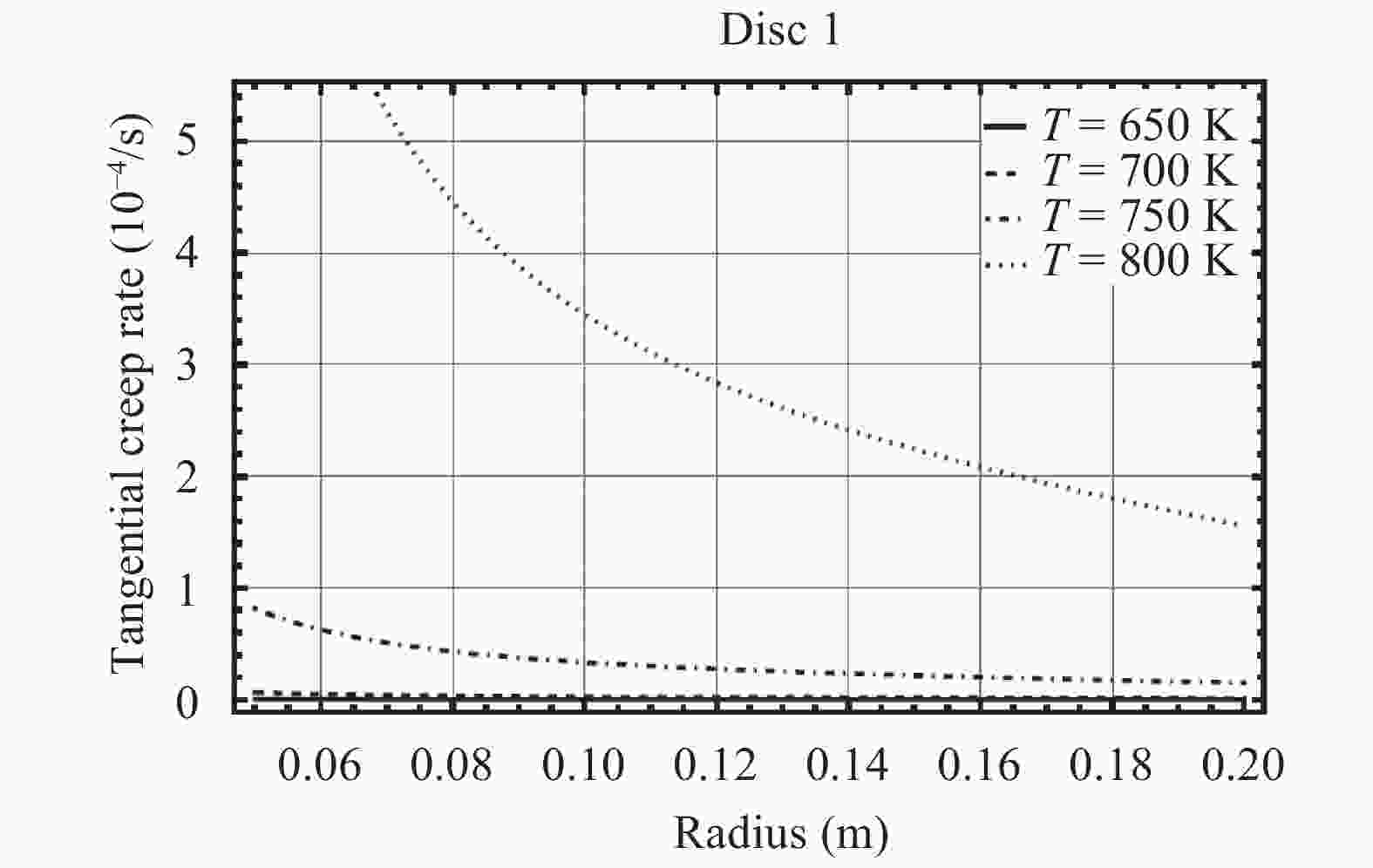
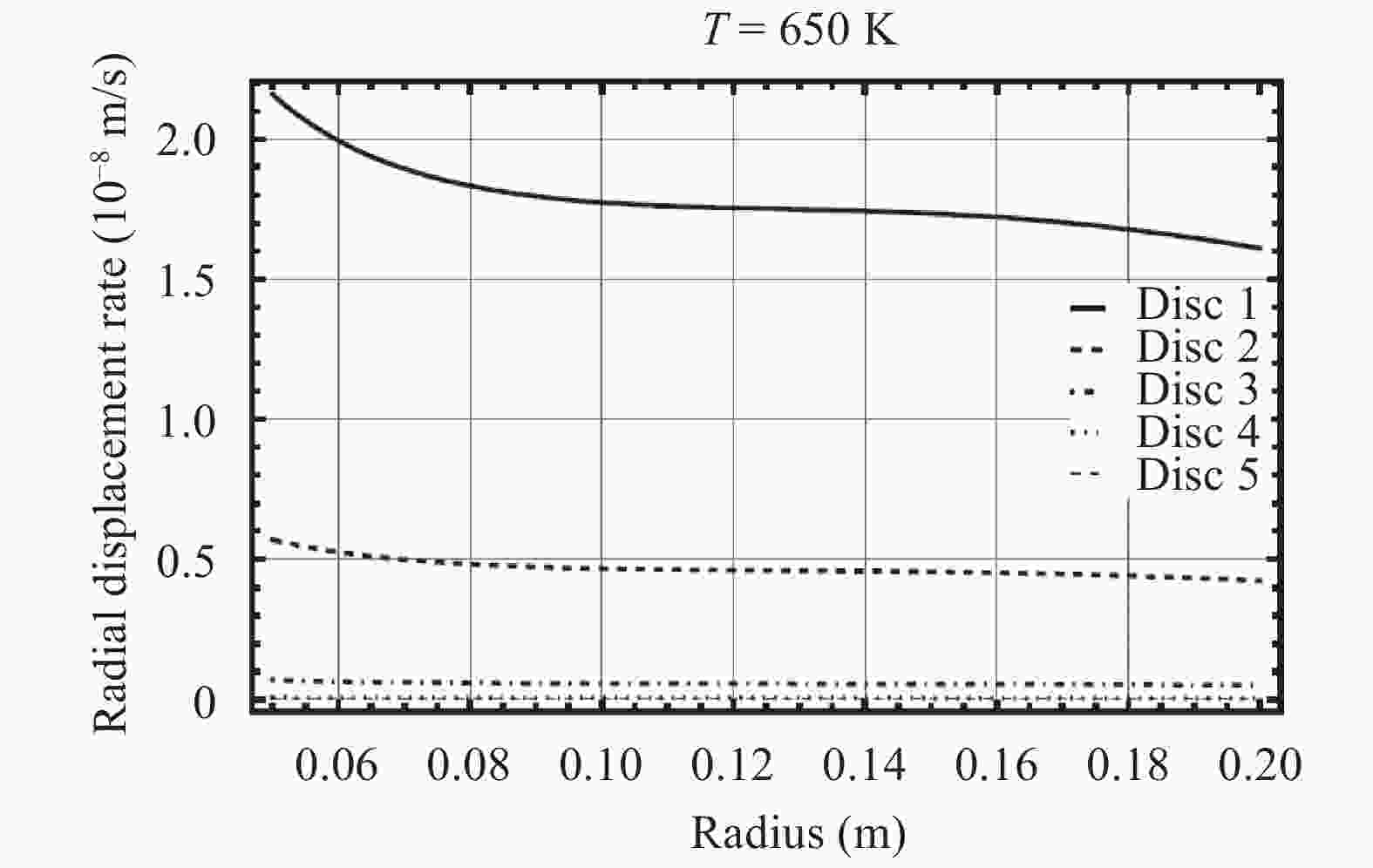
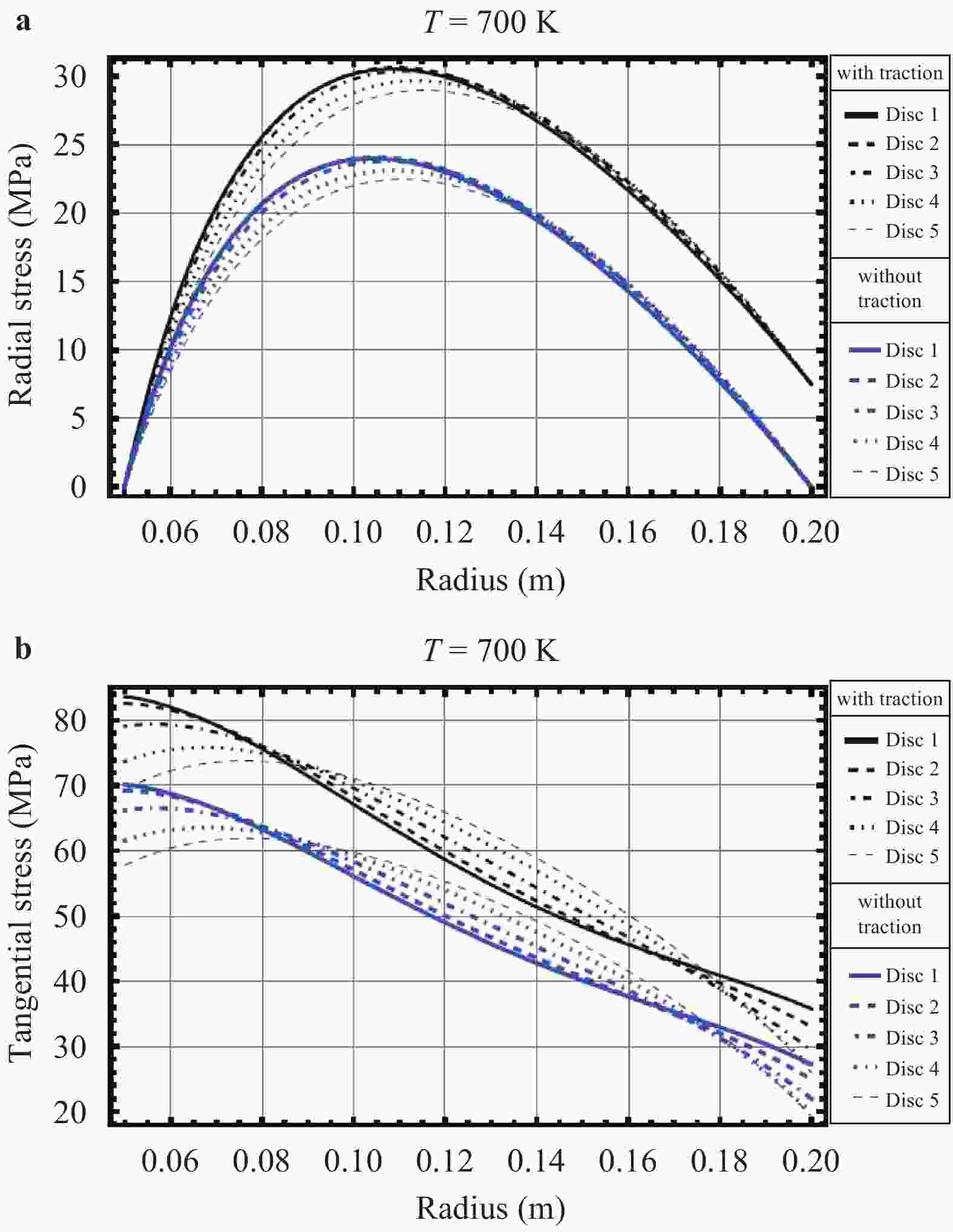
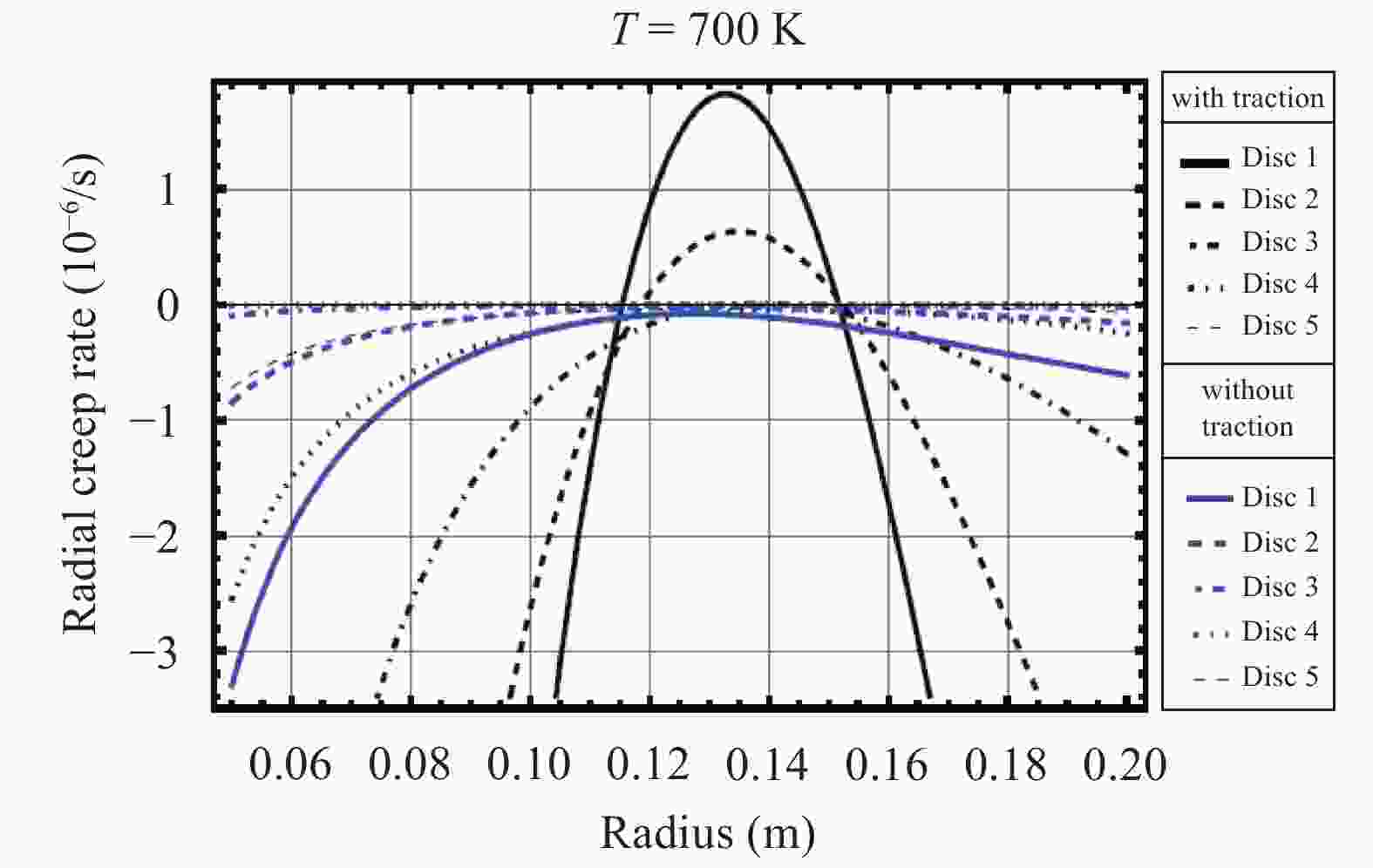
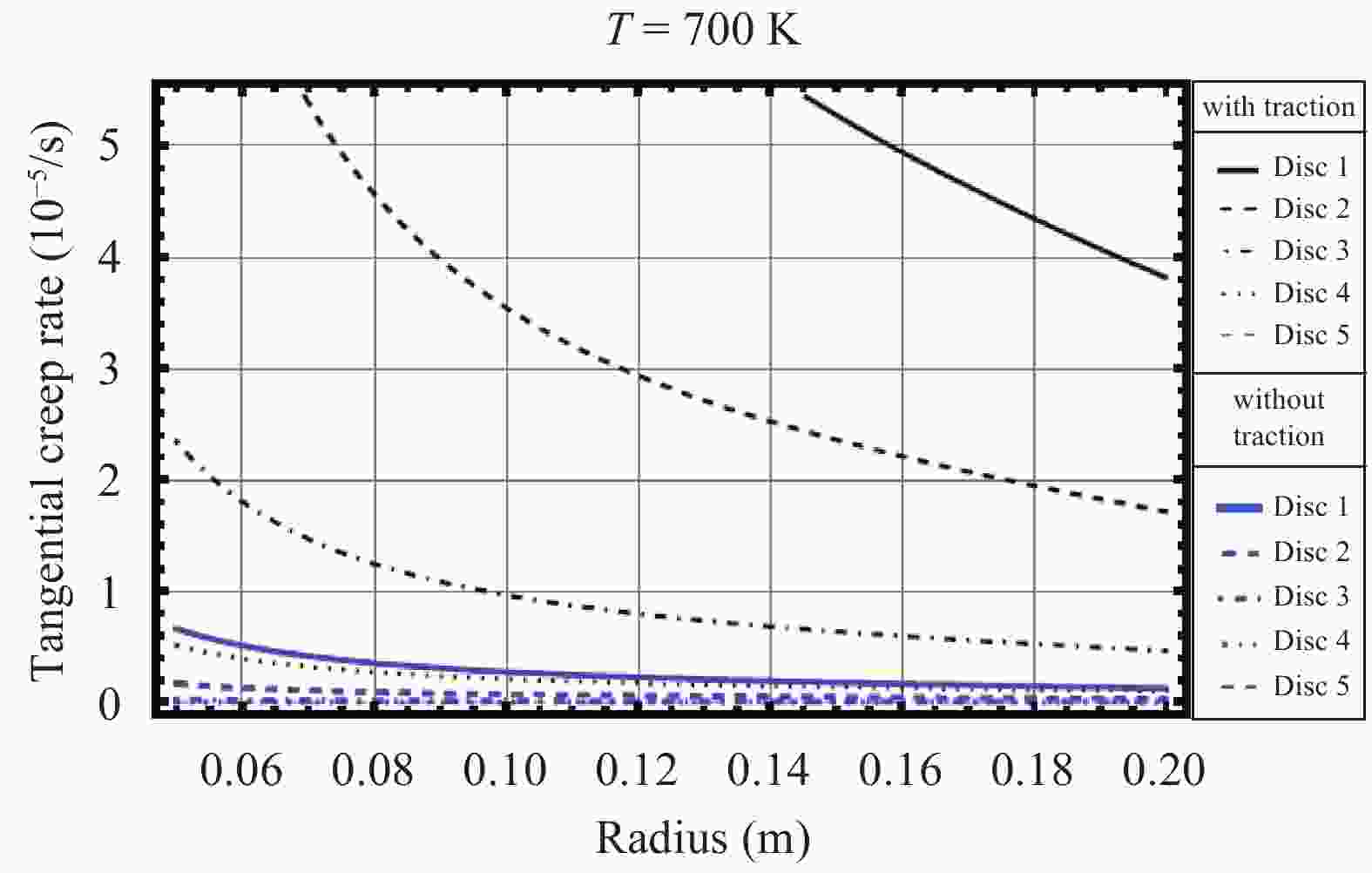
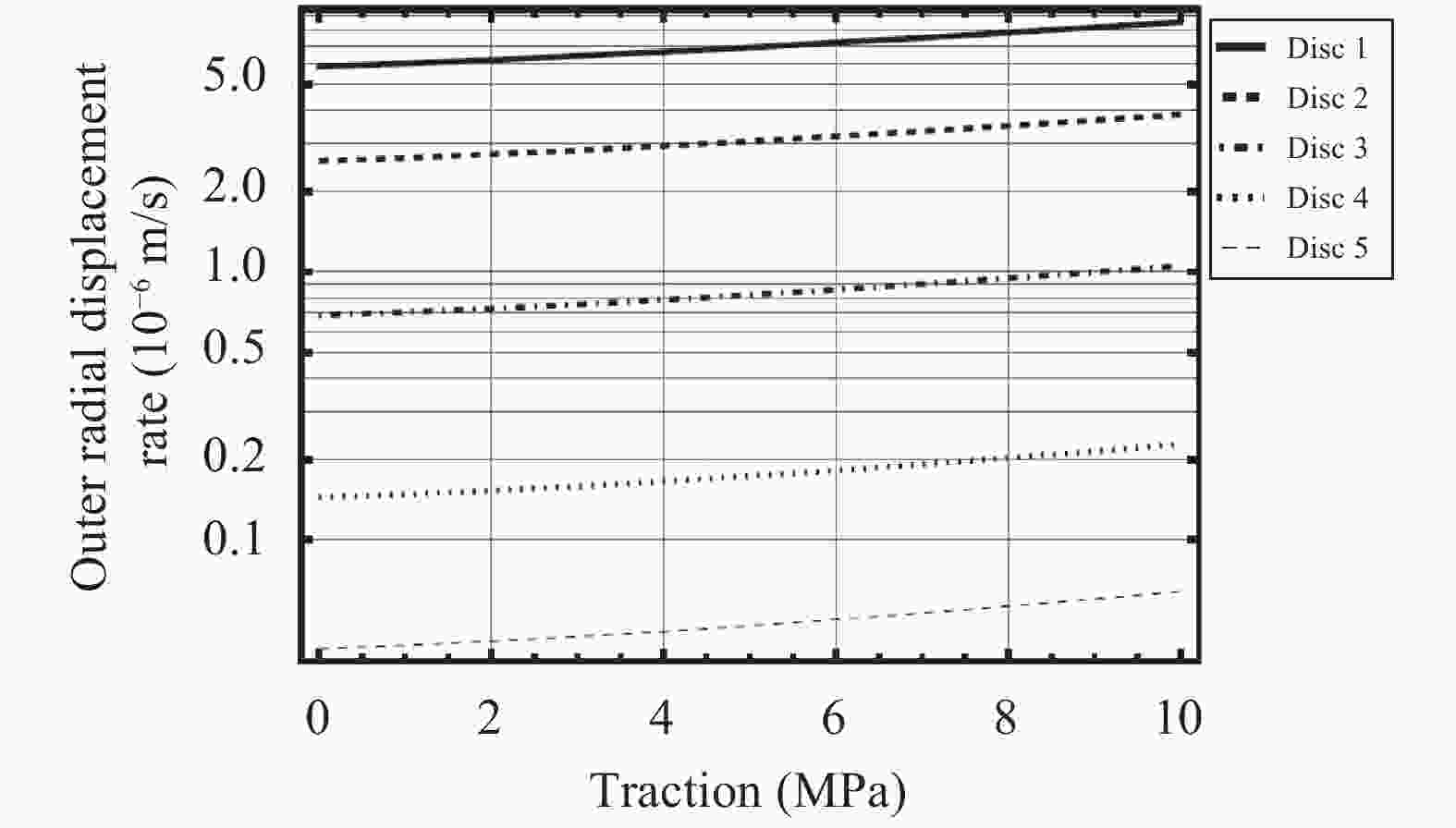
Rotating discs are the vital part of many types of machineries. Usually there is a tendency to make use of them in higher rotational speeds, but ahead of their complete break down the incidence of vibration, plastic failure or creep relaxation can create serious damages which finally prevent the increase of the rotational speed. The invention of new materials has provided new opportunities to increase the loading capacity and speed of the discs. Functionally graded materials (FGMs) are a kind of new materials utilized in the construction of rotating discs. Consequently an important aspect in the analyses of heterogeneous FGM discs is the study of their creep relaxation. One of the well known constitutive equations for the modeling of creep phenomenon is known as the Sherby's law. Based on the steady state creep, the behavior of a variety of FGM rotating discs are studied. The analysis considers the conditions in which the distribution of volume fraction follows a power-law pattern. The required mathematical model and its solution for the analysis of stress and creep strain rate is represented. Some case studies are considered in which the effects of nonlinearly distributed volume fractions are studied. In the case studies, the analysis of rotating FGM discs made of Aluminum-Silicon Carbide compounds is considered. Besides, the analyses of discs with outside tractions are considered and the effects of typical material compositions upon the creep deformations are studied. For instance, the investigation discloses the significance of the use of FGM hubs in the turbine constructions.
Rotating discs are the vital part of many types of machineries. Usually there is a tendency to make use of them in higher rotational speeds, but ahead of their complete break down the incidence of vibration, plastic failure or creep relaxation can create serious damages which finally prevent the increase of the rotational speed. The invention of new materials has provided new opportunities to increase the loading capacity and speed of the discs. Functionally graded materials (FGMs) are a kind of new materials utilized in the construction of rotating discs. Consequently an important aspect in the analyses of heterogeneous FGM discs is the study of their creep relaxation. One of the well known constitutive equations for the modeling of creep phenomenon is known as the Sherby's law. Based on the steady state creep, the behavior of a variety of FGM rotating discs are studied. The analysis considers the conditions in which the distribution of volume fraction follows a power-law pattern. The required mathematical model and its solution for the analysis of stress and creep strain rate is represented. Some case studies are considered in which the effects of nonlinearly distributed volume fractions are studied. In the case studies, the analysis of rotating FGM discs made of Aluminum-Silicon Carbide compounds is considered. Besides, the analyses of discs with outside tractions are considered and the effects of typical material compositions upon the creep deformations are studied. For instance, the investigation discloses the significance of the use of FGM hubs in the turbine constructions.
Theoretical and Applied Mechanics Letters 2019, 9(6): 391-396.
doi: 10.1016/j.taml.2019.06.002
Abstract:
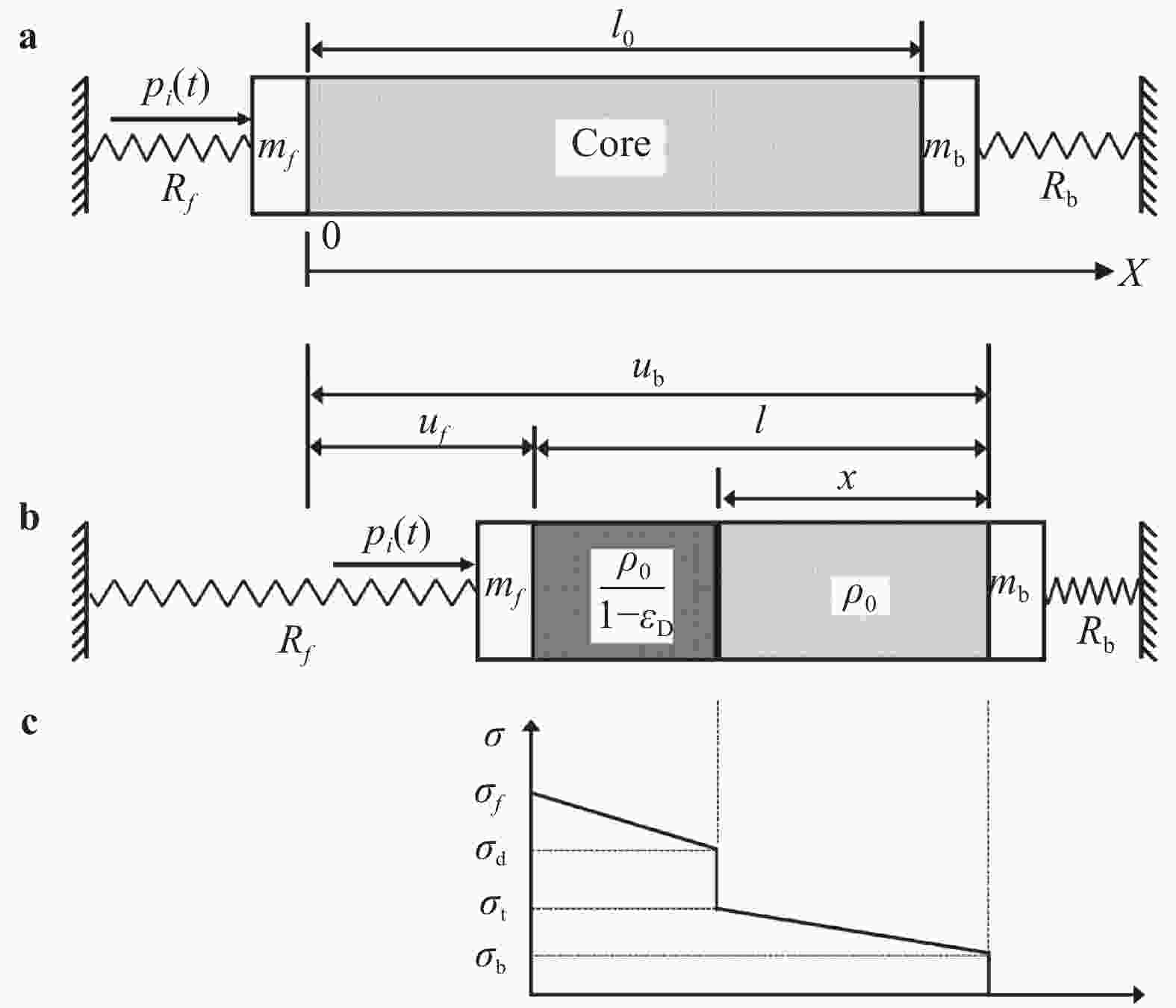
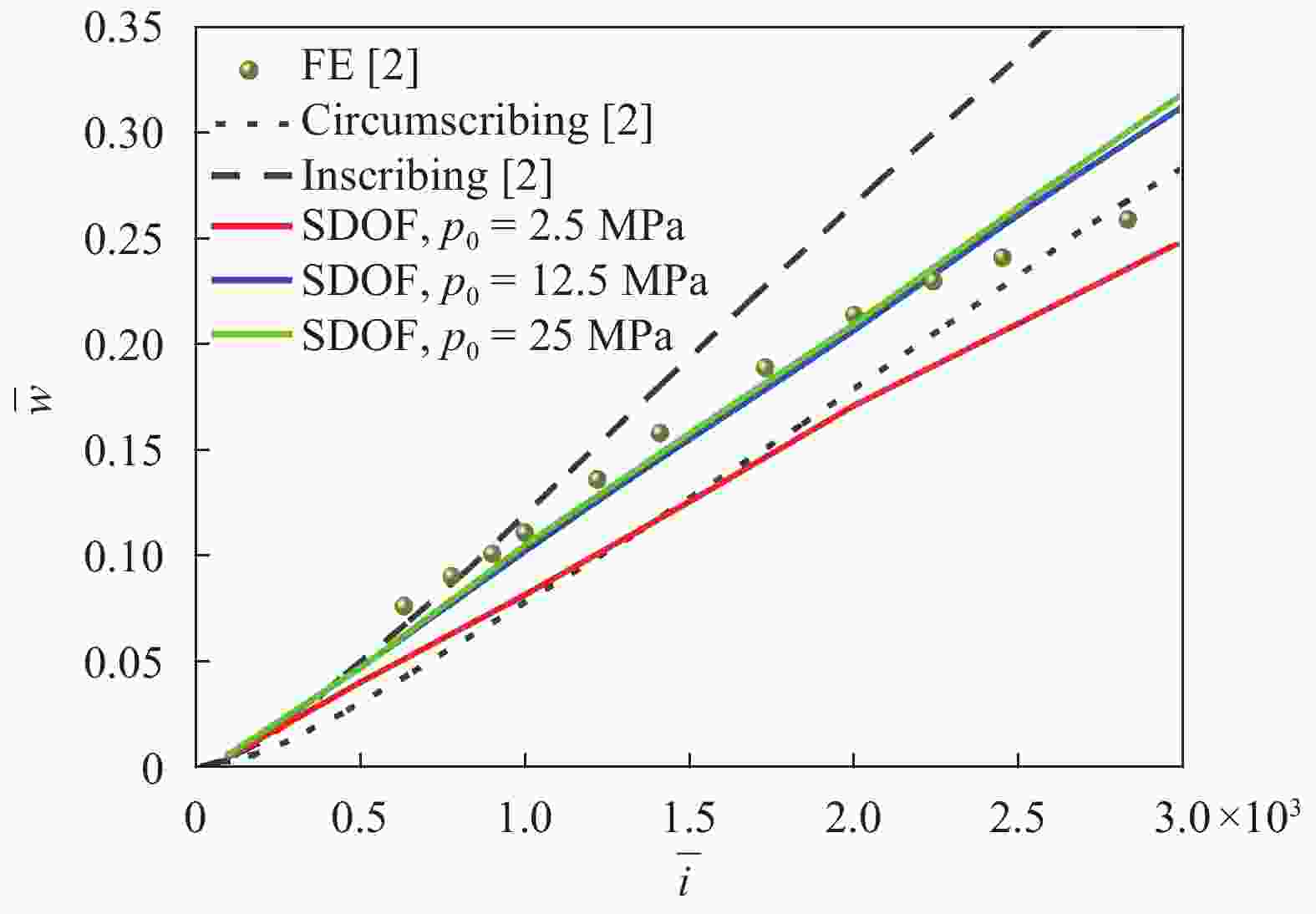
An improved analytical model is developed to predict the dynamic response of clamped lightweight sandwich beams with cellular cores subjected to shock loading over the entire span. The clamped face sheets are simplified as a single-degree-of-freedom (SDOF) system, and the core is idealized using the rigid-perfectly-plastic-locking (RPPL) model. Reflection of incident shock wave is considered by incorporating the bending/stretching resistance of the front face sheet and compaction of the core. The model is validated with existing analytical predictions and FE simulation results, with good agreement achieved. Compared with existing analytical models, the proposed model exhibits superiority in two aspects: the deformation resistance of front face sheet during shock wave reflection is taken into account; the effect of pulse shape is considered. The practical application range of the proposed model is therefore wider.
An improved analytical model is developed to predict the dynamic response of clamped lightweight sandwich beams with cellular cores subjected to shock loading over the entire span. The clamped face sheets are simplified as a single-degree-of-freedom (SDOF) system, and the core is idealized using the rigid-perfectly-plastic-locking (RPPL) model. Reflection of incident shock wave is considered by incorporating the bending/stretching resistance of the front face sheet and compaction of the core. The model is validated with existing analytical predictions and FE simulation results, with good agreement achieved. Compared with existing analytical models, the proposed model exhibits superiority in two aspects: the deformation resistance of front face sheet during shock wave reflection is taken into account; the effect of pulse shape is considered. The practical application range of the proposed model is therefore wider.
Theoretical and Applied Mechanics Letters 2019, 9(6): 397-402.
doi: 10.1016/j.taml.2019.06.003
Abstract:
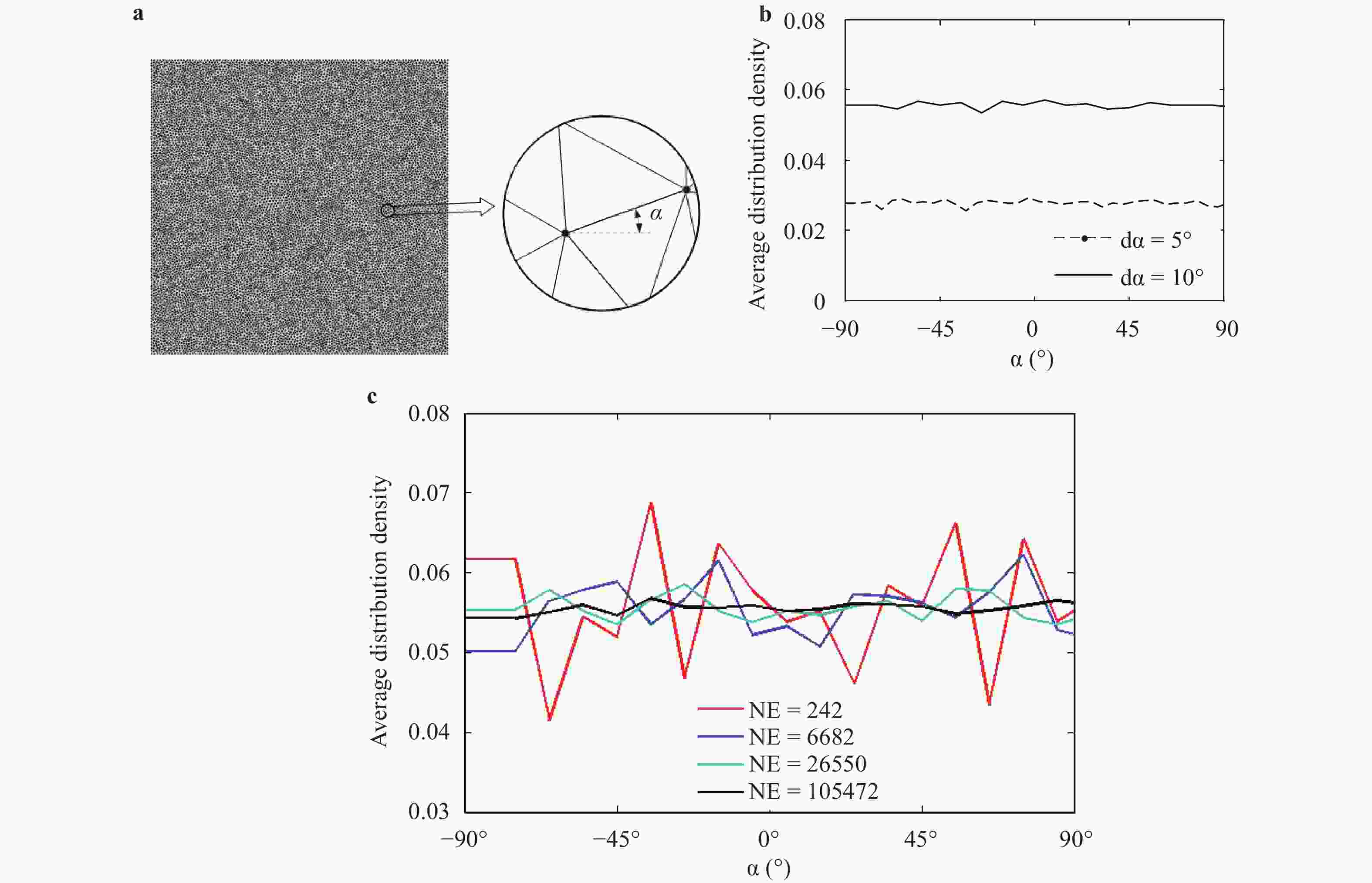
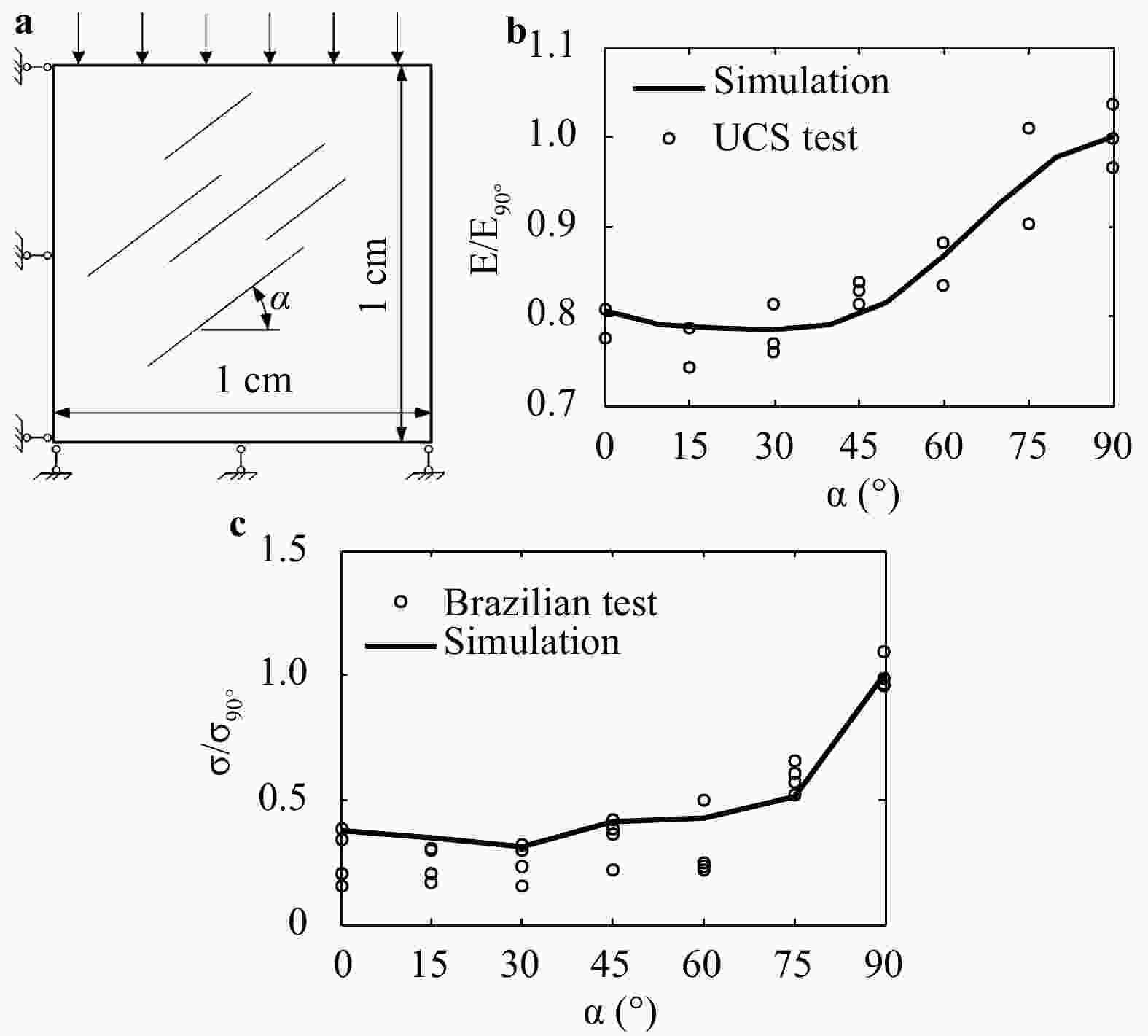
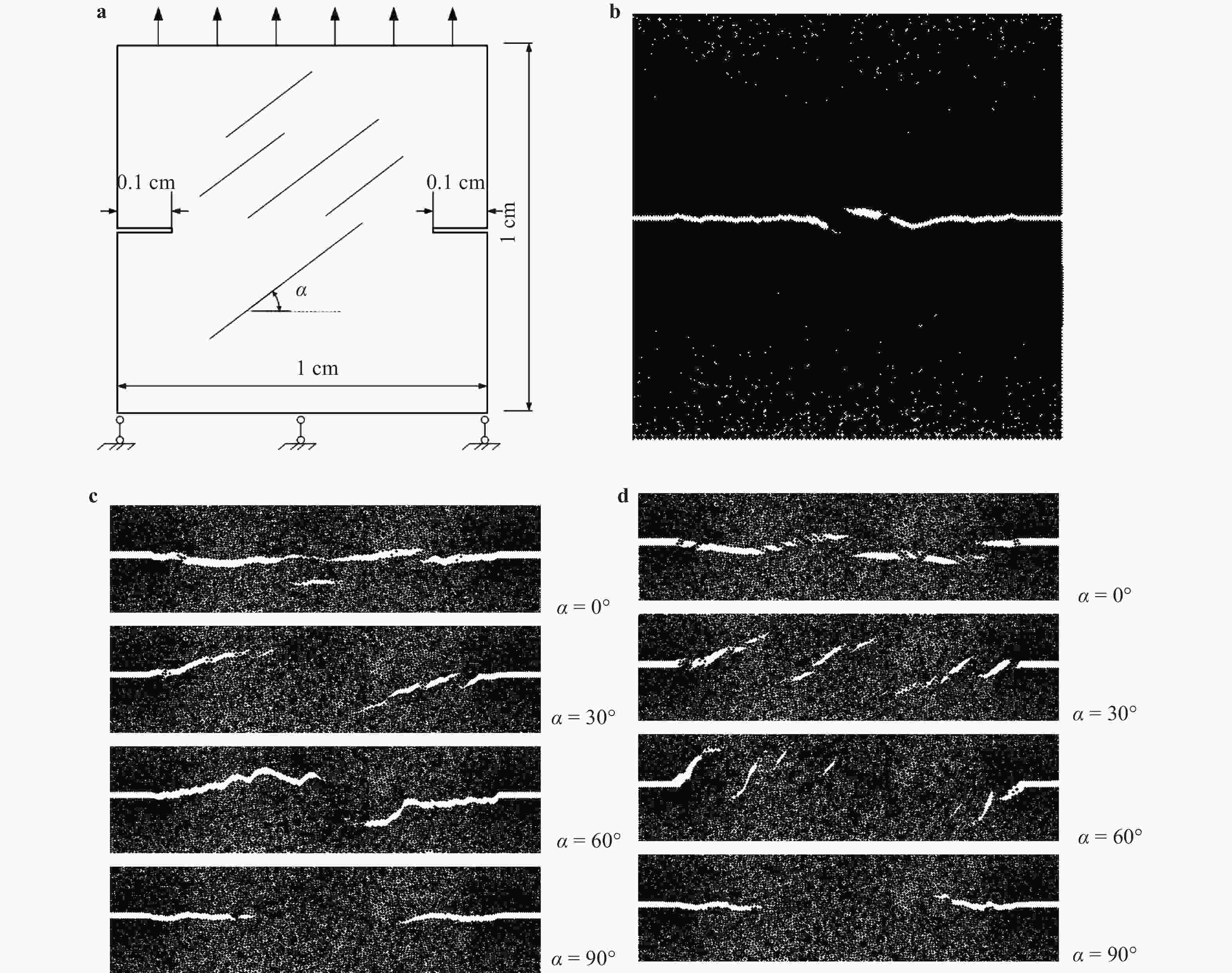
Shale contains distributed directional bedding planes, which make the shale transverse isotropic. To model shale with consideration of the bedding planes, a cohesive finite element method (CFEM) is developed based on the randomized triangular mesh. The interface orientation generated from such mesh tends to be uniformly distributed with the element number increasing. To represent the bedding plane, the interfaces aligned with the bedding plane are assigned the cohesive law that characterizes the bedding plane while the other interfaces are assigned the cohesive law that characterizes the matrix. By this means, the anisotropy characteristics of the stiffness and the strength of shale are well represented. The simulation examples demonstrate that the bedding plane has a significant influence on the fracture trajectory, which is consistent with the observation in the experiment. It is suggested that this modeling method of shale is feasible. It provides an alternative approach to fracture simulation in shale.
Shale contains distributed directional bedding planes, which make the shale transverse isotropic. To model shale with consideration of the bedding planes, a cohesive finite element method (CFEM) is developed based on the randomized triangular mesh. The interface orientation generated from such mesh tends to be uniformly distributed with the element number increasing. To represent the bedding plane, the interfaces aligned with the bedding plane are assigned the cohesive law that characterizes the bedding plane while the other interfaces are assigned the cohesive law that characterizes the matrix. By this means, the anisotropy characteristics of the stiffness and the strength of shale are well represented. The simulation examples demonstrate that the bedding plane has a significant influence on the fracture trajectory, which is consistent with the observation in the experiment. It is suggested that this modeling method of shale is feasible. It provides an alternative approach to fracture simulation in shale.
Theoretical and Applied Mechanics Letters 2019, 9(6): 403-408.
doi: 10.1016/j.taml.2019.06.005
Abstract:
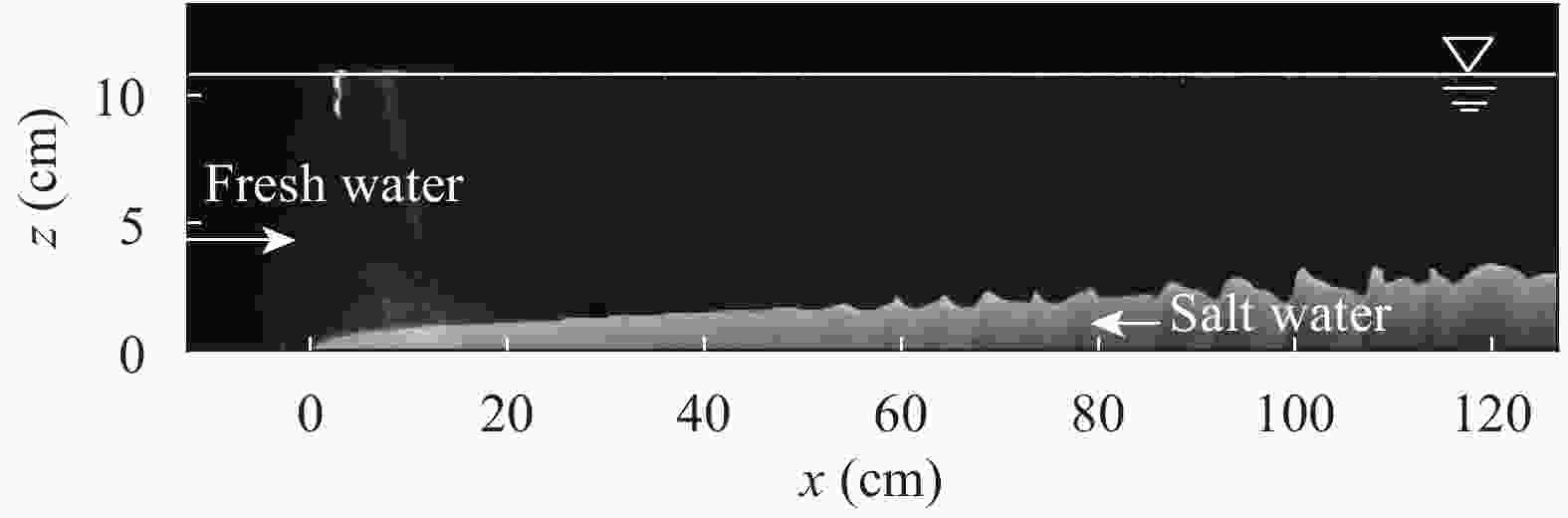
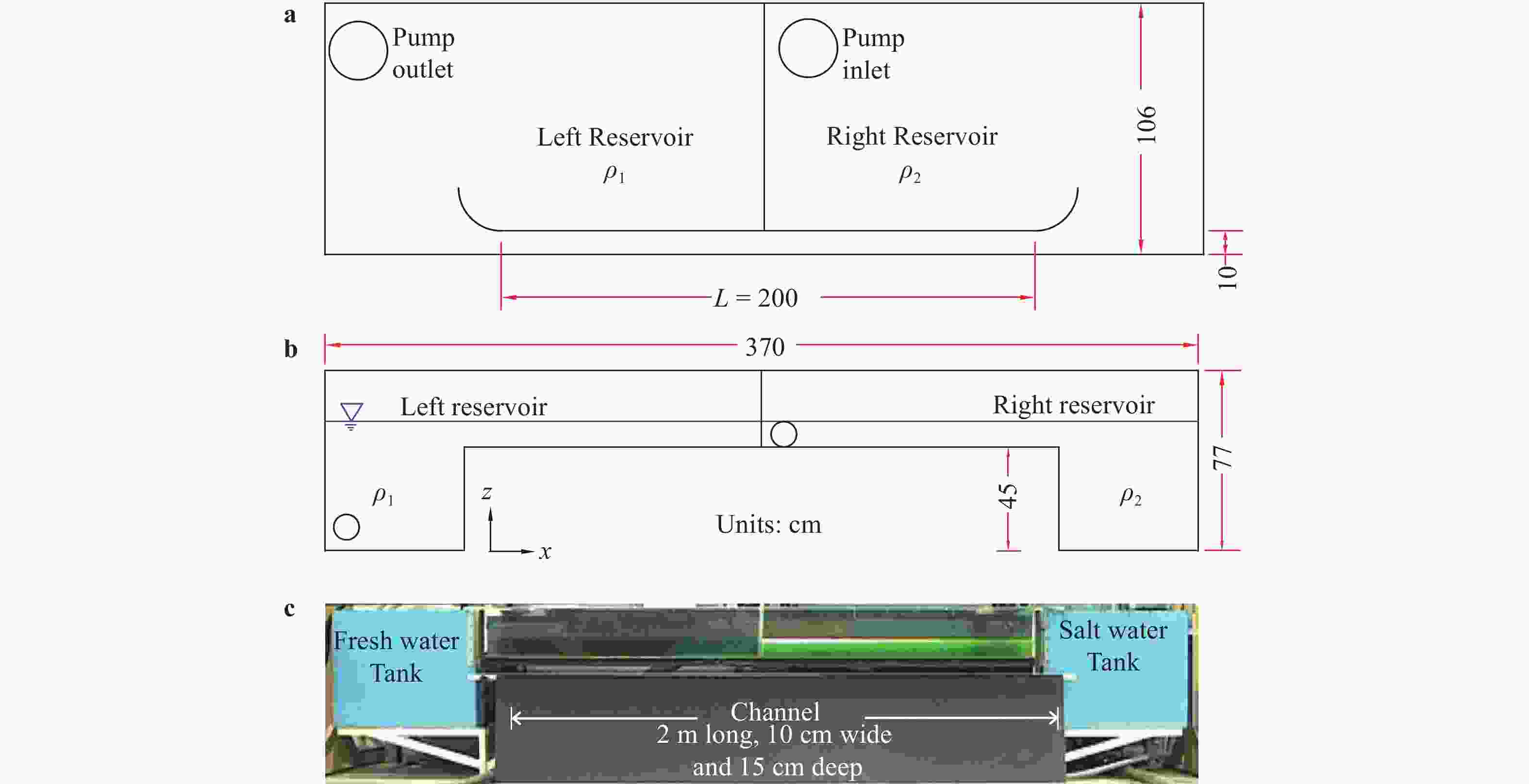
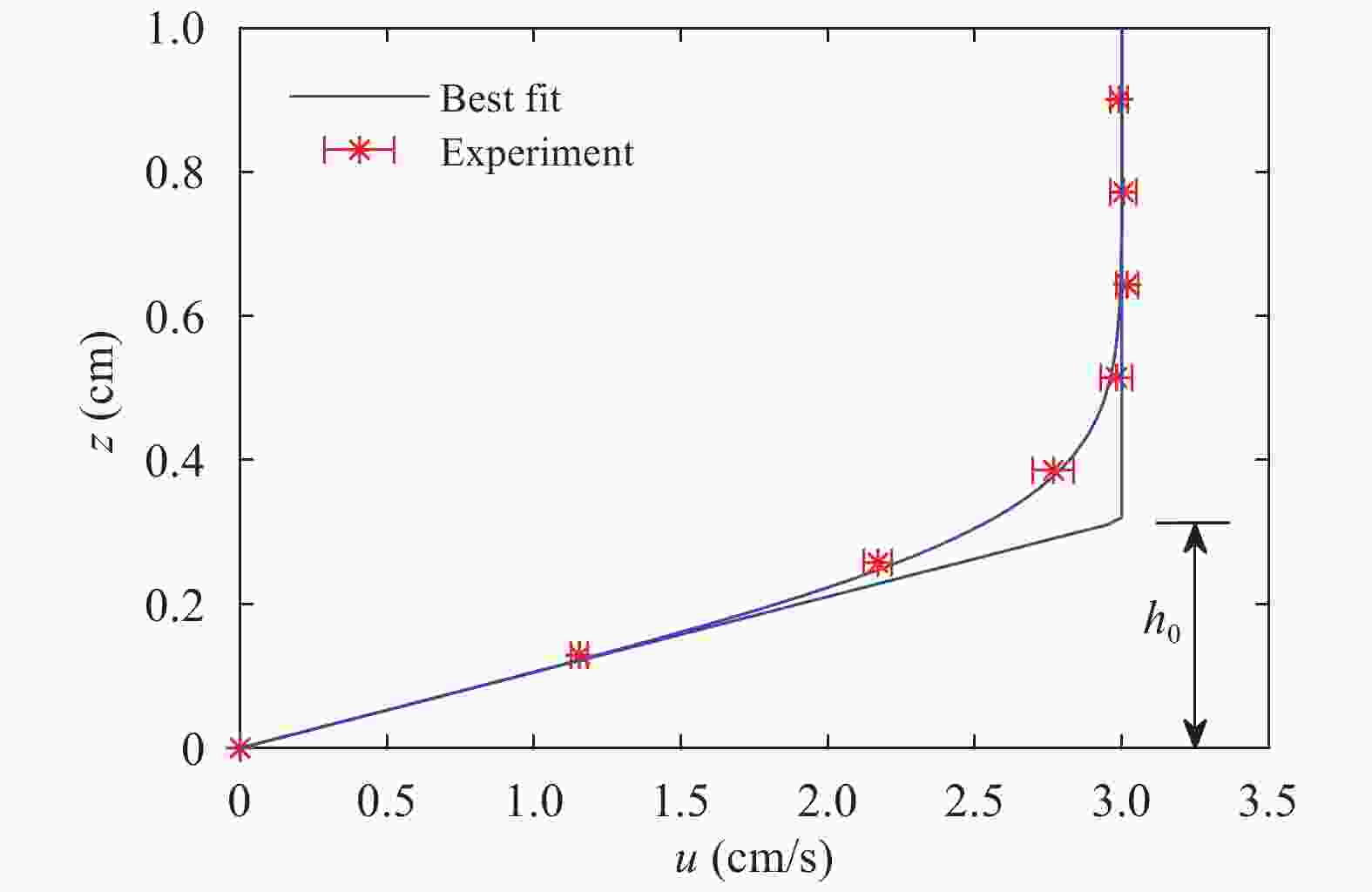
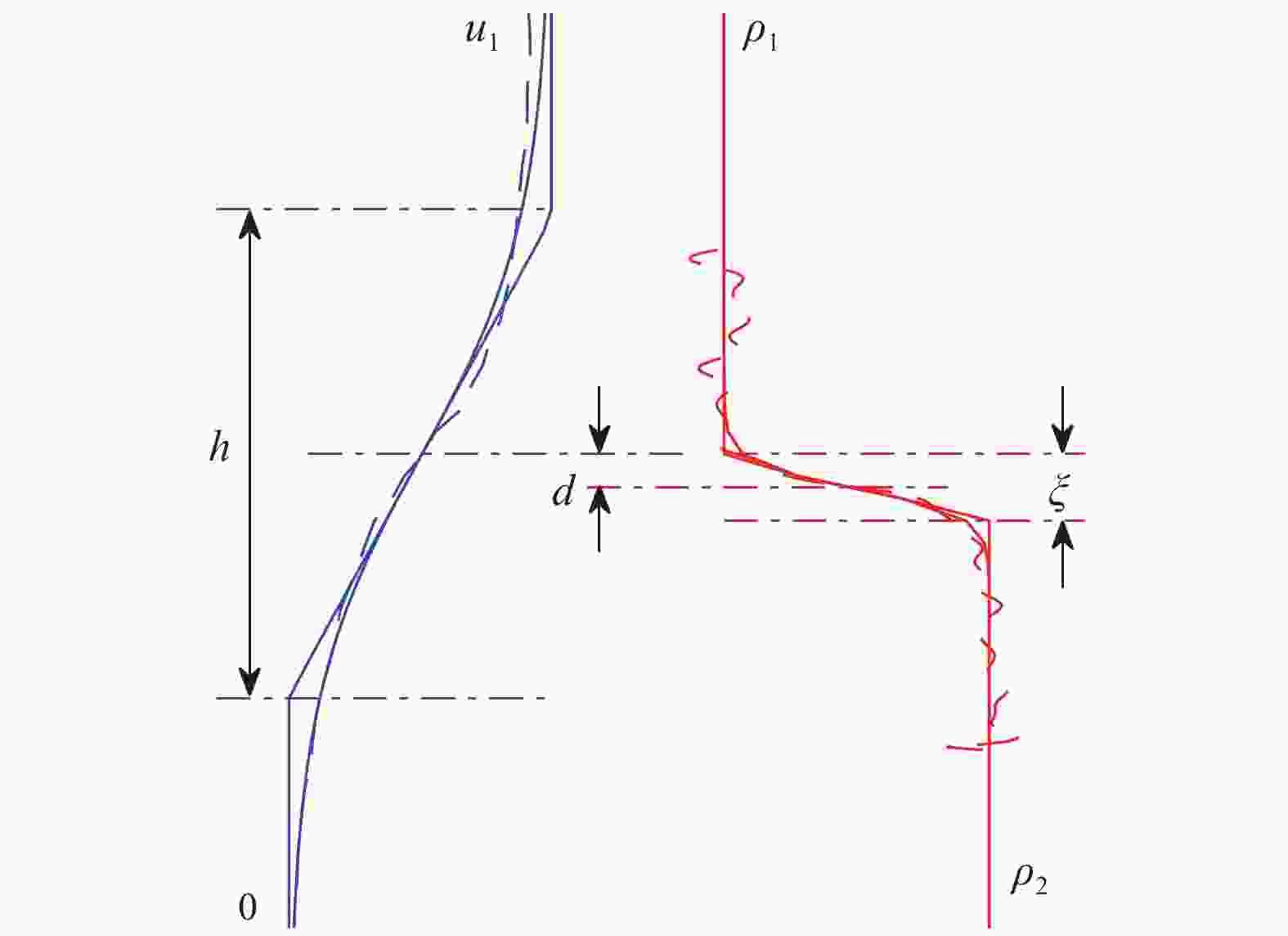
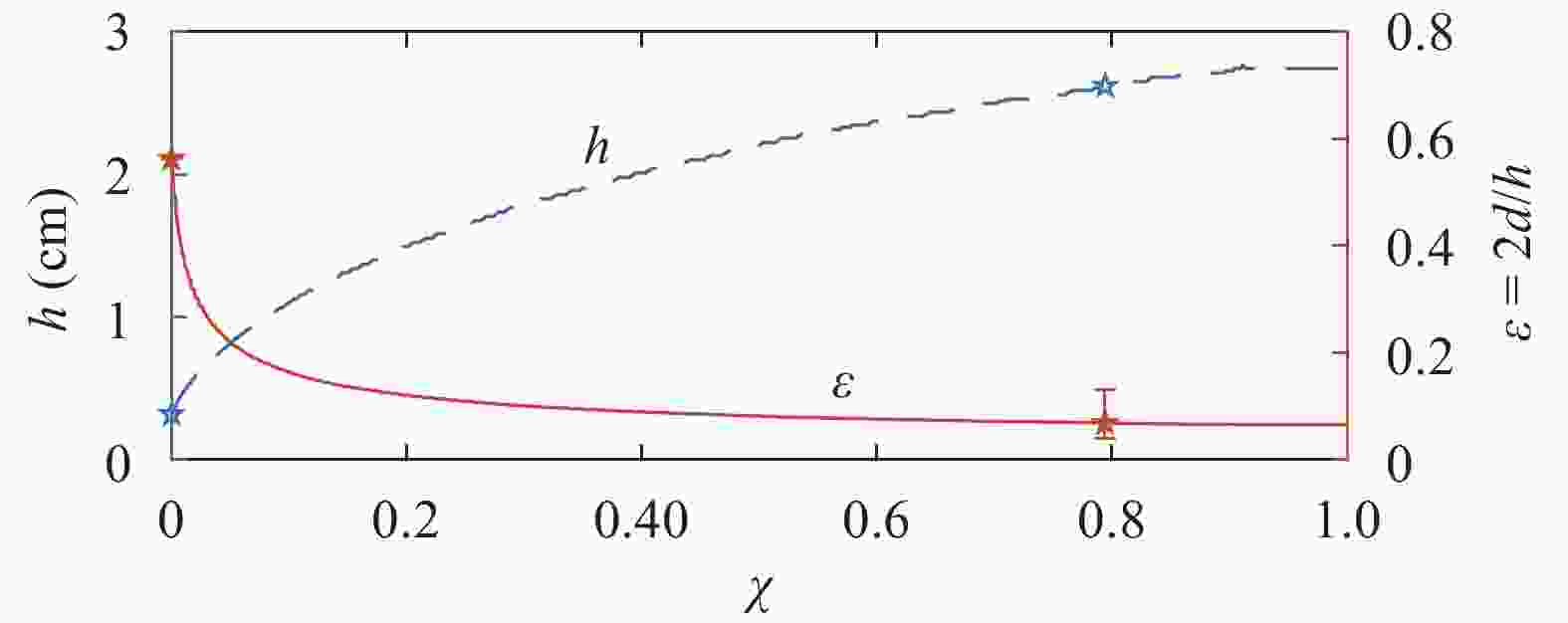
The spatial variation in the properties of an arrested salt wedge have been investigated, both analytically and in the laboratory. In the laboratory particle image velocimetry and laser induced fluorescence were used to obtain flow velocities and the height of the density interface. An analytical solution for the profile of interface height, in the absence of interfacial instabilities, has been developed from two-layer internal hydraulic theory. The evolution of the velocity profile is predicted using a momentum diffusion equation following a Lagrangian frame of reference along the interface of the salt wedge. The centre of the shear layer is predicted to lie above the density interface, with this offset decreasing in the downstream direction. Our theoretical predictions are in good agreement with our laboratory measurements.
The spatial variation in the properties of an arrested salt wedge have been investigated, both analytically and in the laboratory. In the laboratory particle image velocimetry and laser induced fluorescence were used to obtain flow velocities and the height of the density interface. An analytical solution for the profile of interface height, in the absence of interfacial instabilities, has been developed from two-layer internal hydraulic theory. The evolution of the velocity profile is predicted using a momentum diffusion equation following a Lagrangian frame of reference along the interface of the salt wedge. The centre of the shear layer is predicted to lie above the density interface, with this offset decreasing in the downstream direction. Our theoretical predictions are in good agreement with our laboratory measurements.
Theoretical and Applied Mechanics Letters 2019, 9(6): 409-412.
doi: 10.1016/j.taml.2020.01.002
Abstract:
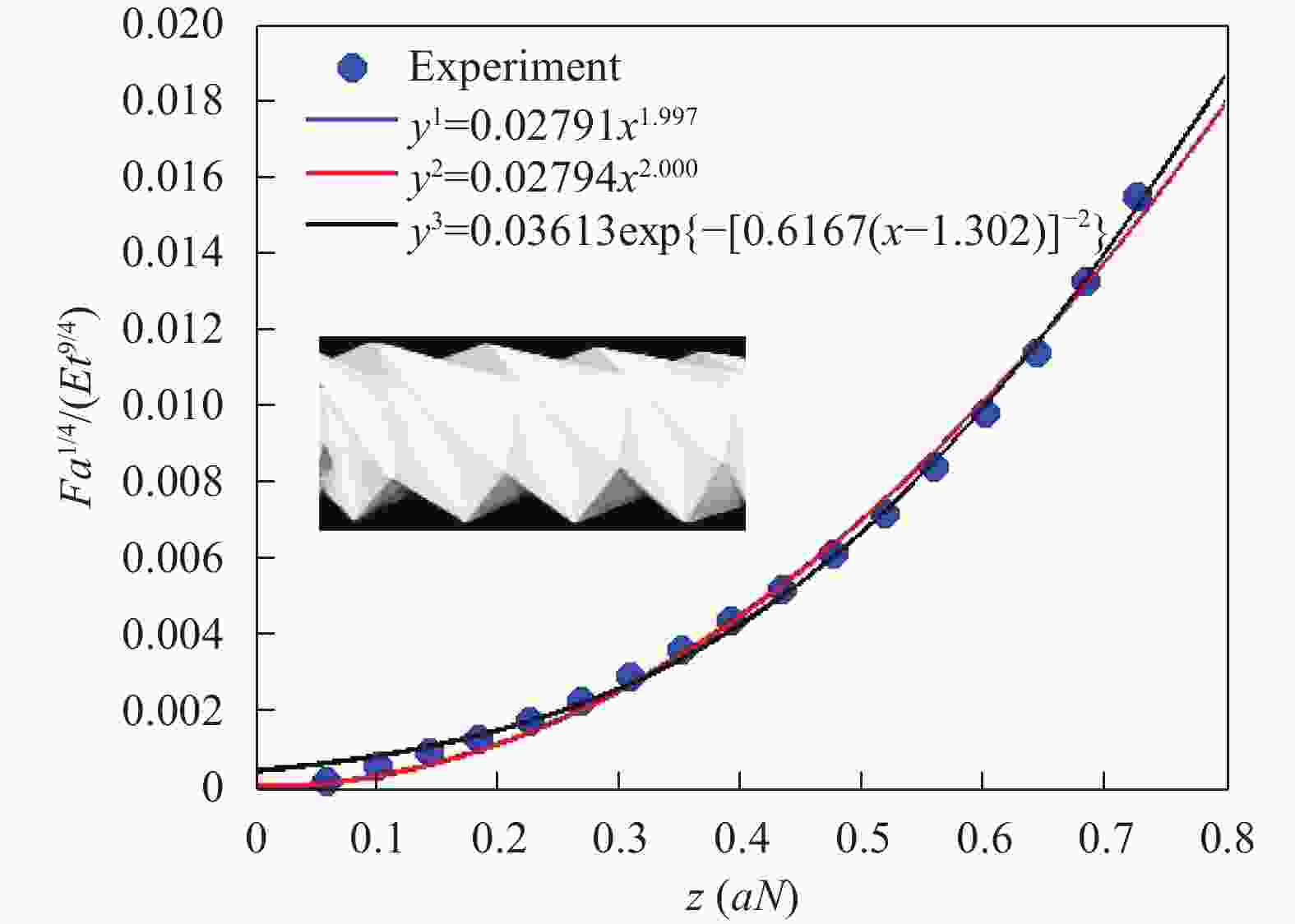
This letter solves an open question of origami paper spring risen by Yoneda et al.(Phys. Rev. E 2019). By using both dimensional analysis and data fitting, an universal scaling law of a paper spring is formulated. The scaling law shows that origami spring force obeys power square law of spring extension, however strong nonlinear to the total twist angle. The study has also successfully generalized the scaling law from the Poisson ratio 0.3 to an arbitrary Poisson's ratio with the help of dimensional analysis.
This letter solves an open question of origami paper spring risen by Yoneda et al.(Phys. Rev. E 2019). By using both dimensional analysis and data fitting, an universal scaling law of a paper spring is formulated. The scaling law shows that origami spring force obeys power square law of spring extension, however strong nonlinear to the total twist angle. The study has also successfully generalized the scaling law from the Poisson ratio 0.3 to an arbitrary Poisson's ratio with the help of dimensional analysis.
 Submit a Paper
Submit a Paper
 Subscription
Subscription
News
MORE+
Call for Papers
MORE+
- Crossing-Mechanics Driven by Big Data
- Machine learning in the fluid mechanics research of wind energy
- Mechanics of Origami/Kirigami structures and metamaterials
- New insights and perspectives on impact biomechanics for human tissues: from injury prevention, protection to protective equipment
- Environmental Mechanics for Extreme Natural Events