Institute of Mechanics,
Chinese Academy of Sciences
2017 Vol.7(5)
column
Display Mode: |
Theoretical and Applied Mechanics Letters 2017, 7(5): 265-268.
doi: 10.1016/j.taml.2017.09.012
Abstract:
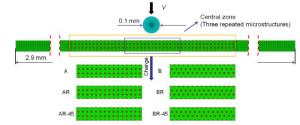
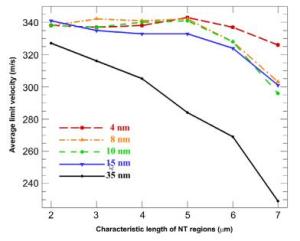
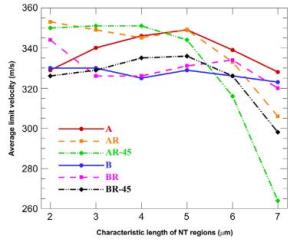
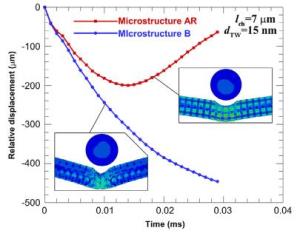
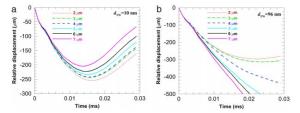
Coarse-grained (CG) metals strengthened by nanotwinned (NT) regions possess high strength and good ductility. As such, they are very suitable for applications in bullet-proof targets. Here, a numerical model based on the conventional theory of strain gradient plasticity and the Johnson-Cook failure criterion is employed to study the influences of volume fraction of NT regions on their ballistic performance. The results show that in general a relatively small twin spacing (4-10 nm) and a moderate volume fraction (7%-20%) will lead to excellent limit velocity and that the influences of volume fraction on limit displacement change with the category of impact processes.
Coarse-grained (CG) metals strengthened by nanotwinned (NT) regions possess high strength and good ductility. As such, they are very suitable for applications in bullet-proof targets. Here, a numerical model based on the conventional theory of strain gradient plasticity and the Johnson-Cook failure criterion is employed to study the influences of volume fraction of NT regions on their ballistic performance. The results show that in general a relatively small twin spacing (4-10 nm) and a moderate volume fraction (7%-20%) will lead to excellent limit velocity and that the influences of volume fraction on limit displacement change with the category of impact processes.
Theoretical and Applied Mechanics Letters 2017, 7(5): 269-275.
doi: 10.1016/j.taml.2017.11.001
Abstract:
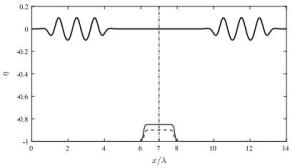
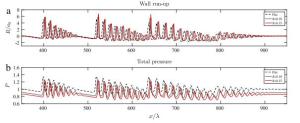
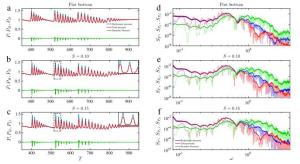
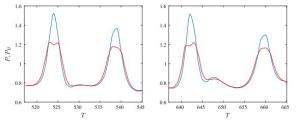
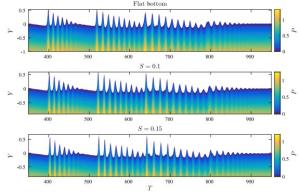
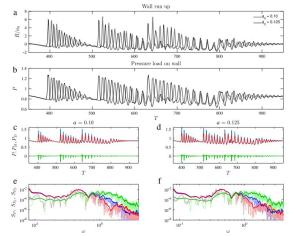
The pressure load at a vertical barrier caused by extreme wave run-up is analysed numerically, using the conformal mapping method to solve the two-dimensional free surface Euler equations in a pseudospectral model. Previously this problem has been examined in the case of a flat-bottomed geometry. Here, the model is extended to consider a varying bathymetry. Numerical experiments show that an increasing step-like bottom profile may enhance the extreme run-up of long waves but result in a reduced pressure load.
The pressure load at a vertical barrier caused by extreme wave run-up is analysed numerically, using the conformal mapping method to solve the two-dimensional free surface Euler equations in a pseudospectral model. Previously this problem has been examined in the case of a flat-bottomed geometry. Here, the model is extended to consider a varying bathymetry. Numerical experiments show that an increasing step-like bottom profile may enhance the extreme run-up of long waves but result in a reduced pressure load.
Theoretical and Applied Mechanics Letters 2017, 7(5): 276-279.
doi: 10.1016/j.taml.2017.09.009
Abstract:
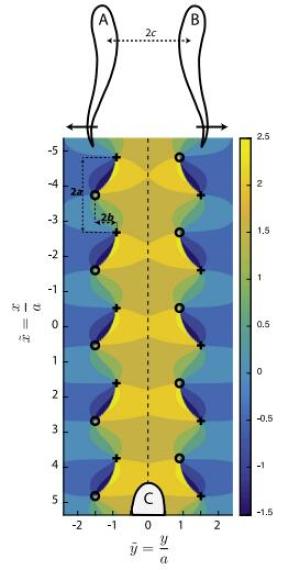
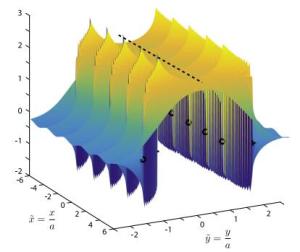
The "Lighthill conjecture" regarding passive forces created in a group of self-propelled objects moving in an inviscid fluid is examined. We show that pressure gradients are produced in the wakes of anterior members of the group, which both indicate and assist rear members to stay in advantageous positions, for saving energy.
The "Lighthill conjecture" regarding passive forces created in a group of self-propelled objects moving in an inviscid fluid is examined. We show that pressure gradients are produced in the wakes of anterior members of the group, which both indicate and assist rear members to stay in advantageous positions, for saving energy.
Theoretical and Applied Mechanics Letters 2017, 7(5): 280-285.
doi: 10.1016/j.taml.2017.10.001
Abstract:
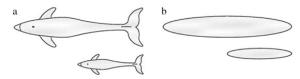
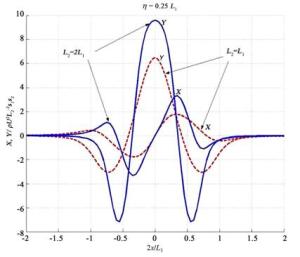
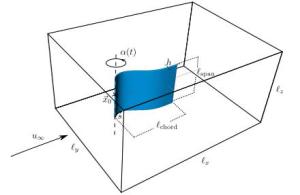
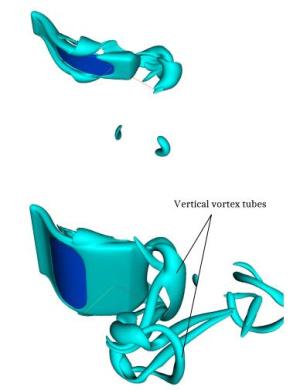
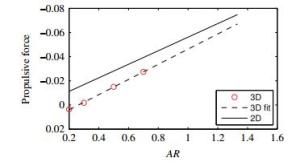
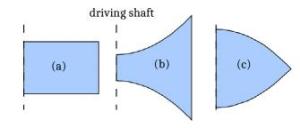
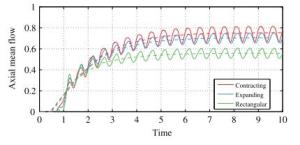
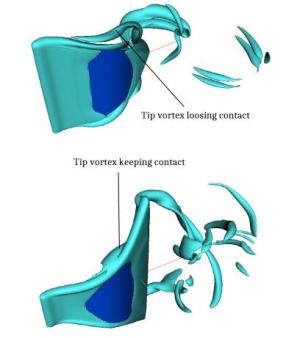
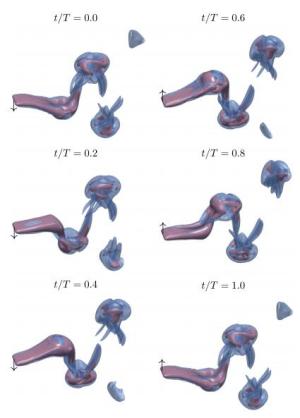
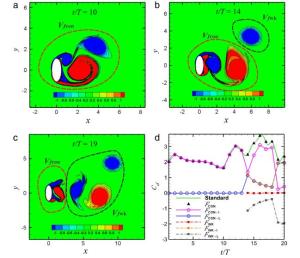
We present numerical simulations of simplified models for swimming organisms or robots, using chordwise flexible elastic plates. We focus on the tip vortices originating from three-dimensional effects due to the finite span of the plate. These effects play an important role when predicting the swimmer's cruising velocity, since they contribute significantly to the drag force. First we simulate swimmers with rectangular plates of different aspect ratios and compare the results with a recent experimental study. Then we consider plates with expanding and contracting shapes. We find the cruising velocity of the contracting swimmer to be higher than the rectangular one, which in turn is higher than the expanding one. We provide some evidence that this result is due to the tip vortices interacting differently with the swimmer.
We present numerical simulations of simplified models for swimming organisms or robots, using chordwise flexible elastic plates. We focus on the tip vortices originating from three-dimensional effects due to the finite span of the plate. These effects play an important role when predicting the swimmer's cruising velocity, since they contribute significantly to the drag force. First we simulate swimmers with rectangular plates of different aspect ratios and compare the results with a recent experimental study. Then we consider plates with expanding and contracting shapes. We find the cruising velocity of the contracting swimmer to be higher than the rectangular one, which in turn is higher than the expanding one. We provide some evidence that this result is due to the tip vortices interacting differently with the swimmer.
Theoretical and Applied Mechanics Letters 2017, 7(5): 286-291.
doi: 10.1016/j.taml.2017.09.006
Abstract:
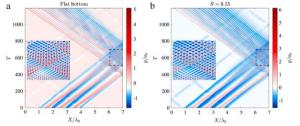
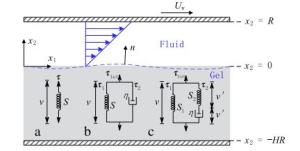
We study instability of a Newtonian Couette flow past a gel-like film in the limit of vanishing Reynolds number. Three models are explored including one hyperelastic (neo-Hookean) solid, and two viscoelastic (Kelvin-Voigt and Zener) solids. Instead of using the conventional Lagrangian description in the solid phase for solving the displacement field, we construct equivalent "differential" models in an Eulerian reference frame, and solve for the velocity, pressure, and stress in both fluid and solid phases simultaneously. We find the interfacial instability is driven by the first-normal stress difference in the basestate solution in both hyperelastic and viscoelastic models. For the neo-Hookean solid, when subjected to a shear flow, the interface exhibits a short-wave (finite-wavelength) instability when the film is thin (thick). In the Kelvin-Voigt and Zener solids where viscous effects are incorporated, instability growth is enhanced at small wavenumber but suppressed at large wavenumber, leading to a dominant finitewavelength instability. In addition, adding surface tension effectively stabilizes the interface to sustain fluid shear.
We study instability of a Newtonian Couette flow past a gel-like film in the limit of vanishing Reynolds number. Three models are explored including one hyperelastic (neo-Hookean) solid, and two viscoelastic (Kelvin-Voigt and Zener) solids. Instead of using the conventional Lagrangian description in the solid phase for solving the displacement field, we construct equivalent "differential" models in an Eulerian reference frame, and solve for the velocity, pressure, and stress in both fluid and solid phases simultaneously. We find the interfacial instability is driven by the first-normal stress difference in the basestate solution in both hyperelastic and viscoelastic models. For the neo-Hookean solid, when subjected to a shear flow, the interface exhibits a short-wave (finite-wavelength) instability when the film is thin (thick). In the Kelvin-Voigt and Zener solids where viscous effects are incorporated, instability growth is enhanced at small wavenumber but suppressed at large wavenumber, leading to a dominant finitewavelength instability. In addition, adding surface tension effectively stabilizes the interface to sustain fluid shear.
Theoretical and Applied Mechanics Letters 2017, 7(5): 292-300.
doi: 10.1016/j.taml.2017.09.011
Abstract:
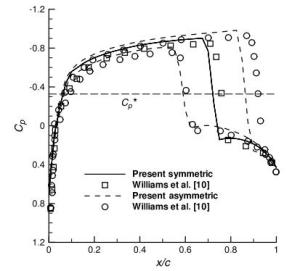
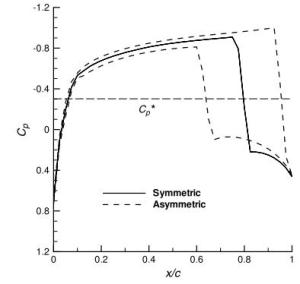
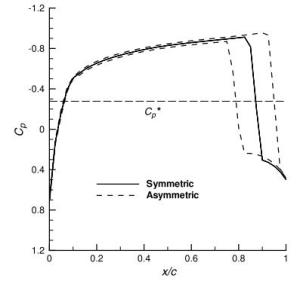
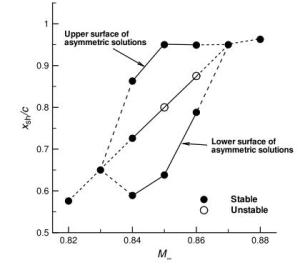
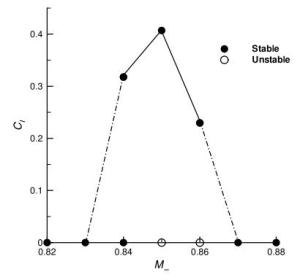
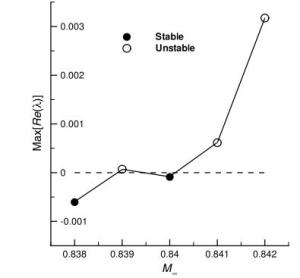
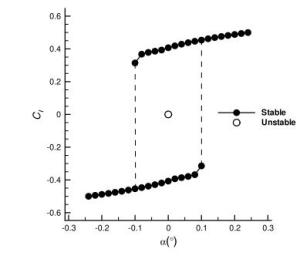
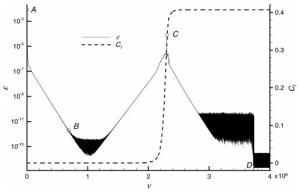
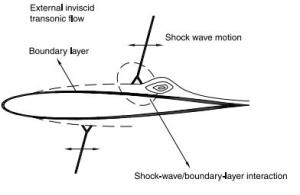
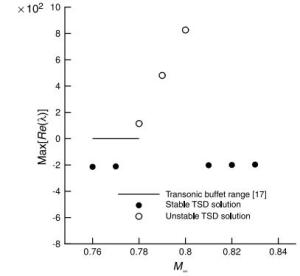
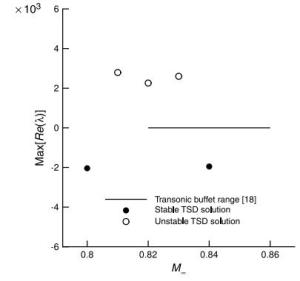
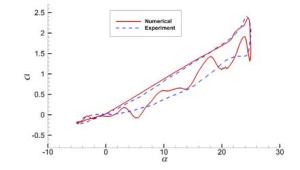
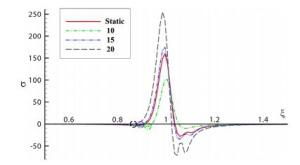
Numerical solutions of the steady transonic small-disturbance (TSD) potential equation are computed using the conservative Murman-Cole scheme. Multiple solutions are discovered and mapped out for the Mach number range at zero angle of attack and the angle of attack range at Mach number 0.85 for the NACA 0012 airfoil. We present a linear stability analysis method by directly assembling and evaluating the Jacobian matrix of the nonlinear finite-difference equation of the TSD equation. The stability of all the discovered multiple solutions are then determined by the proposed eigen analysis. The relation of stability to convergence of the iterative method for solving the TSD equation is discussed. Computations and the stability analysis demonstrate the possibility of eliminating the multiple solutions and stabilizing the remaining unique solution by adding a sufficiently long splitter plate downstream the airfoil trailing edge. Finally, instability of the solution of the TSD equation is shown to be closely connected to the onset of transonic buffet by comparing with experimental data.
Numerical solutions of the steady transonic small-disturbance (TSD) potential equation are computed using the conservative Murman-Cole scheme. Multiple solutions are discovered and mapped out for the Mach number range at zero angle of attack and the angle of attack range at Mach number 0.85 for the NACA 0012 airfoil. We present a linear stability analysis method by directly assembling and evaluating the Jacobian matrix of the nonlinear finite-difference equation of the TSD equation. The stability of all the discovered multiple solutions are then determined by the proposed eigen analysis. The relation of stability to convergence of the iterative method for solving the TSD equation is discussed. Computations and the stability analysis demonstrate the possibility of eliminating the multiple solutions and stabilizing the remaining unique solution by adding a sufficiently long splitter plate downstream the airfoil trailing edge. Finally, instability of the solution of the TSD equation is shown to be closely connected to the onset of transonic buffet by comparing with experimental data.
Theoretical and Applied Mechanics Letters 2017, 7(5): 301-305.
doi: 10.1016/j.taml.2017.09.010
Abstract:
We review the concept of "equilibrium" in turbulence. It generally means a property of the energy spectrum, it can also be understood in terms of a scalar property, the Taylor-Kolmogorov formula relating the dissipation rate to the total energy and integral length scale. The implications of equilibrium and strong departure from equilibrium for turbulence modeling are stressed.
We review the concept of "equilibrium" in turbulence. It generally means a property of the energy spectrum, it can also be understood in terms of a scalar property, the Taylor-Kolmogorov formula relating the dissipation rate to the total energy and integral length scale. The implications of equilibrium and strong departure from equilibrium for turbulence modeling are stressed.
Theoretical and Applied Mechanics Letters 2017, 7(5): 306-310.
doi: 10.1016/j.taml.2017.11.003
Abstract:
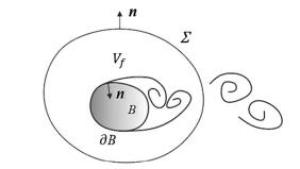
We extend the impulse theory for unsteady aerodynamics, from its classic global form to finite-domain formulation, then to a minimum-domain version for discrete wake. Each extension has been confirmed numerically. The minimum-domain theory indicates that the numerical finding of Li and Lu (2012) is of general significance:The entire force is completely determined by only the time rate of impulse of those vortical structures still connecting to the body, along with the Lamb-vector integral thereof that captures the contribution of all the rest disconnected vortical structures.
We extend the impulse theory for unsteady aerodynamics, from its classic global form to finite-domain formulation, then to a minimum-domain version for discrete wake. Each extension has been confirmed numerically. The minimum-domain theory indicates that the numerical finding of Li and Lu (2012) is of general significance:The entire force is completely determined by only the time rate of impulse of those vortical structures still connecting to the body, along with the Lamb-vector integral thereof that captures the contribution of all the rest disconnected vortical structures.
Theoretical and Applied Mechanics Letters 2017, 7(5): 311-315.
doi: 10.1016/j.taml.2017.11.004
Abstract:
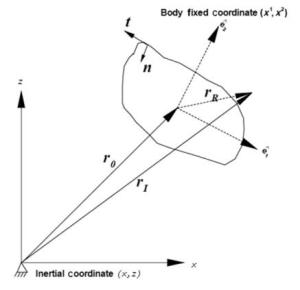
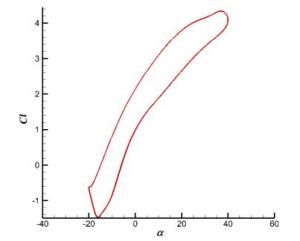
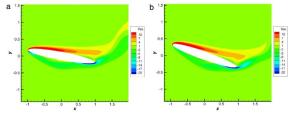
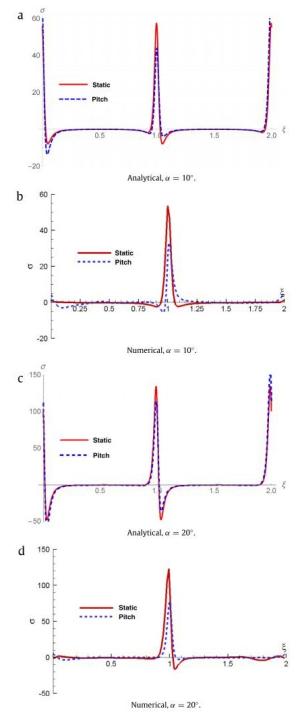
Why the stall of an airfoil can be significantly delayed by its pitching-up motion? Various attempts have been proposed to answer this question over the past half century, but none is satisfactory. In this letter we prove that a chain of vorticity-dynamics processes at accelerating boundary is fully responsible for the causal mechanism underlying this peculiar phenomenon. The local flow behavior is explained by a simple potential-flow model.
Why the stall of an airfoil can be significantly delayed by its pitching-up motion? Various attempts have been proposed to answer this question over the past half century, but none is satisfactory. In this letter we prove that a chain of vorticity-dynamics processes at accelerating boundary is fully responsible for the causal mechanism underlying this peculiar phenomenon. The local flow behavior is explained by a simple potential-flow model.
 Submit a Paper
Submit a Paper
 Subscription
Subscription
News
MORE+
Call for Papers
MORE+
- Crossing-Mechanics Driven by Big Data
- Machine learning in the fluid mechanics research of wind energy
- Mechanics of Origami/Kirigami structures and metamaterials
- New insights and perspectives on impact biomechanics for human tissues: from injury prevention, protection to protective equipment
- Environmental Mechanics for Extreme Natural Events