Institute of Mechanics,
Chinese Academy of Sciences
2017 Vol.7(3)
Display Mode: |
Theoretical and Applied Mechanics Letters 2017, 7(3): 121-125.
doi: 10.1016/j.taml.2017.02.004
Abstract:
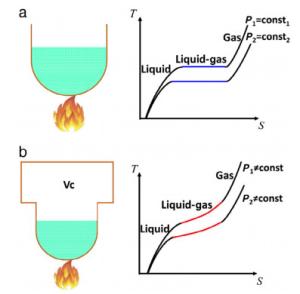
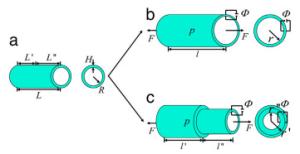
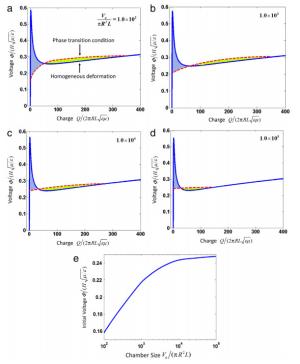
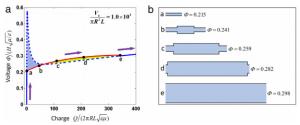
The electromechanical phase transition for a dielectric elastomer (DE) tube has been demonstrated in recent experiments, where it is found that the unbulged phase gradually changed into bulged phase. Previous theoretical works only studied the transition process under pressure control condition, which is not consistent with the real experimental condition. This paper focuses on more complex features of the electromechanical phase transition under internal pressure of constant mass. We derive the equilibrium equations and the condition for coexistent states for a DE tube under an internal pressure, a voltage through the thickness and an axial force. We find that under mass control condition the voltage needed to maintain the phase transition increases as the process proceeds. We analyze the entire process of electromechanical phase transition and find that the evolution of configurations is also different from that for pressure control condition.
The electromechanical phase transition for a dielectric elastomer (DE) tube has been demonstrated in recent experiments, where it is found that the unbulged phase gradually changed into bulged phase. Previous theoretical works only studied the transition process under pressure control condition, which is not consistent with the real experimental condition. This paper focuses on more complex features of the electromechanical phase transition under internal pressure of constant mass. We derive the equilibrium equations and the condition for coexistent states for a DE tube under an internal pressure, a voltage through the thickness and an axial force. We find that under mass control condition the voltage needed to maintain the phase transition increases as the process proceeds. We analyze the entire process of electromechanical phase transition and find that the evolution of configurations is also different from that for pressure control condition.
Theoretical and Applied Mechanics Letters 2017, 7(3): 126-133.
doi: 10.1016/j.taml.2017.01.006
Abstract:
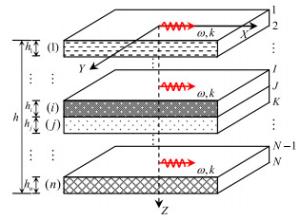
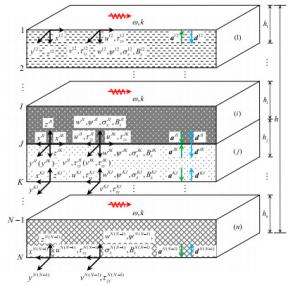
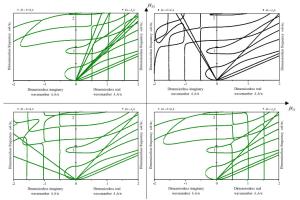
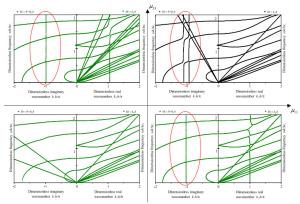
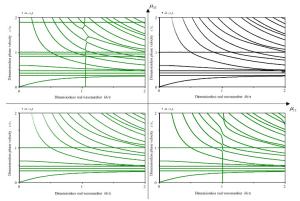
With the advent of left-handed magnetic materials, it is desirable to develop high-performance wave devices based on their novel properties of wave propagation. This letter reports the special properties of elastic wave propagation in magnetoelastic multilayered composites with negative permeability as compared to those in counterpart structures with positive permeability. These novel properties of elastic waves are discerned from the diversified dispersion curves, which represent the propagation and attenuation characteristics of elastic waves. To compute these dispersion curves, the method of reverberation-ray matrix is extended for the analysis of elastic waves in magnetoelastic multilayered composites. Although only the results of a single piezomagnetic and a binary magnetoelastic layers with mechanically free and magnetically short surfaces as well as perfect interface are illustrated in the numerical examples, the analysis is applicable to magnetoelastic multilayered structures with other kinds of boundaries/interfaces.
With the advent of left-handed magnetic materials, it is desirable to develop high-performance wave devices based on their novel properties of wave propagation. This letter reports the special properties of elastic wave propagation in magnetoelastic multilayered composites with negative permeability as compared to those in counterpart structures with positive permeability. These novel properties of elastic waves are discerned from the diversified dispersion curves, which represent the propagation and attenuation characteristics of elastic waves. To compute these dispersion curves, the method of reverberation-ray matrix is extended for the analysis of elastic waves in magnetoelastic multilayered composites. Although only the results of a single piezomagnetic and a binary magnetoelastic layers with mechanically free and magnetically short surfaces as well as perfect interface are illustrated in the numerical examples, the analysis is applicable to magnetoelastic multilayered structures with other kinds of boundaries/interfaces.
Theoretical and Applied Mechanics Letters 2017, 7(3): 134-137.
doi: 10.1016/j.taml.2017.02.006
Abstract:
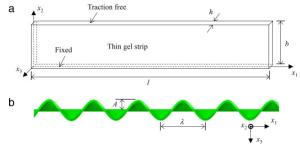
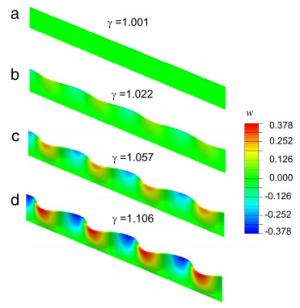
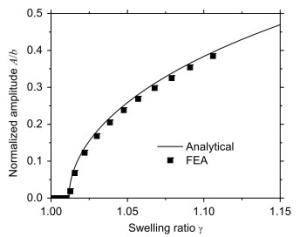
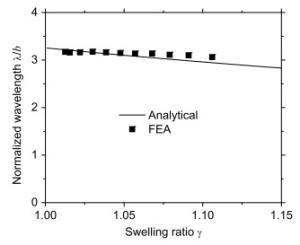
The buckling of thin gel film has attracted much attention due to its applications in the design of threedimensional structure from two-dimensional template. We have established an analytical model to study the swelling-induced buckling of a thin gel strip with one edge clamped and the others free. The closed-form solutions for the amplitude and wavelength of the buckled shape are obtained by energy minimization of the total potential energy. The analytical results agree well with finite element analysis based on the inhomogeneous gel theory without any parameter fitting. The model provides a route to study complex postbuckling behaviors of thin gel films and guidelines to design the buckled configuration quantitatively by controlling the swelling ratio.
The buckling of thin gel film has attracted much attention due to its applications in the design of threedimensional structure from two-dimensional template. We have established an analytical model to study the swelling-induced buckling of a thin gel strip with one edge clamped and the others free. The closed-form solutions for the amplitude and wavelength of the buckled shape are obtained by energy minimization of the total potential energy. The analytical results agree well with finite element analysis based on the inhomogeneous gel theory without any parameter fitting. The model provides a route to study complex postbuckling behaviors of thin gel films and guidelines to design the buckled configuration quantitatively by controlling the swelling ratio.
Theoretical and Applied Mechanics Letters 2017, 7(3): 138-144.
doi: 10.1016/j.taml.2017.04.002
Abstract:
We present second-order expressions for the free-surface elevation, velocity potential and pressure resulting from the interaction of surface waves in water of arbitrary depth. When the surface waves have nearly equal frequencies and nearly opposite directions, a second-order pressure can be felt all the way to the sea bottom. There are at least two areas of applications: reflective structures and microseisms. Microseisms generated by water waves in the ocean are small vibrations of the ground resulting from pressure oscillations associated with the coupling of ocean surface gravity waves and the sea floor. They are recorded on land-based seismic stations throughout the world and they are divided into primary and secondary types, as a function of spectral content. Secondary microseisms are generated by the interaction of surface waves with nearly equal frequencies and nearly opposite directions. The efficiency of microseism generation thus depends in part on ocean wave frequency and direction. Based on the second-order expressions for the dynamic pressure, a simple theoretical analysis that quantifies the degree of nearness in amplitude, frequency, and incidence angle, which must be reached to observe the phenomenon, is presented.
We present second-order expressions for the free-surface elevation, velocity potential and pressure resulting from the interaction of surface waves in water of arbitrary depth. When the surface waves have nearly equal frequencies and nearly opposite directions, a second-order pressure can be felt all the way to the sea bottom. There are at least two areas of applications: reflective structures and microseisms. Microseisms generated by water waves in the ocean are small vibrations of the ground resulting from pressure oscillations associated with the coupling of ocean surface gravity waves and the sea floor. They are recorded on land-based seismic stations throughout the world and they are divided into primary and secondary types, as a function of spectral content. Secondary microseisms are generated by the interaction of surface waves with nearly equal frequencies and nearly opposite directions. The efficiency of microseism generation thus depends in part on ocean wave frequency and direction. Based on the second-order expressions for the dynamic pressure, a simple theoretical analysis that quantifies the degree of nearness in amplitude, frequency, and incidence angle, which must be reached to observe the phenomenon, is presented.
Theoretical and Applied Mechanics Letters 2017, 7(3): 145-151.
doi: 10.1016/j.taml.2017.05.003
Abstract:
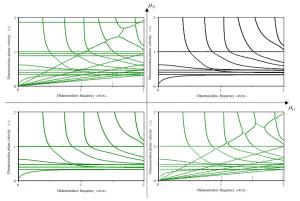
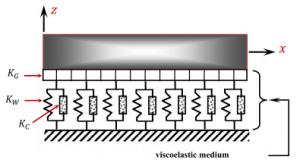
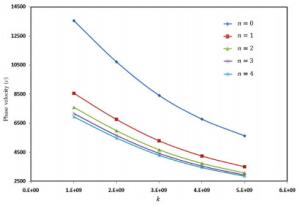
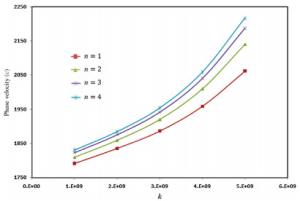
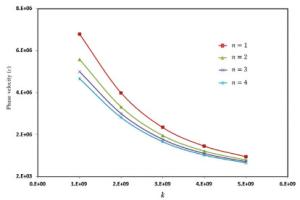
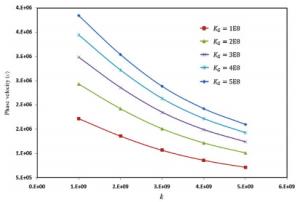
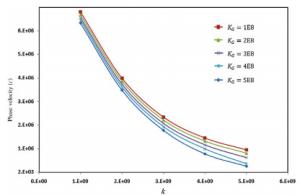
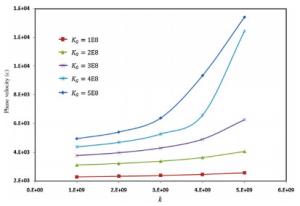
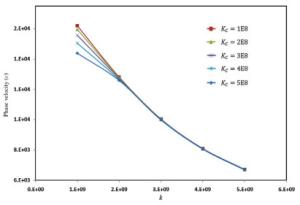
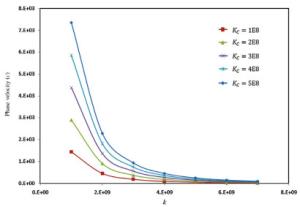
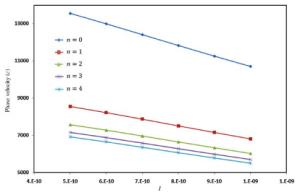
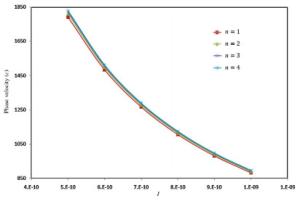
Wave propagation analysis for a functionally graded nanobeam with rectangular cross-section resting on visco-Pasternak's foundation is studied in this paper. Timoshenko's beam model and nonlocal elasticity theory are employed for formulation of the problem. The equations of motion are derived using Hamilton's principals by calculating kinetic energy, strain energy and work due to viscoelastic foundation. The effects of various parameters such as wavenumber, non-homogeneous index, nonlocal parameter and three parameters of foundation are performed on the phase velocity of the nanobeam. The obtained results indicate that some parameters such as non-homogeneous index, nonlocal parameter and wavenumber have significant effect on the response of the system.
Wave propagation analysis for a functionally graded nanobeam with rectangular cross-section resting on visco-Pasternak's foundation is studied in this paper. Timoshenko's beam model and nonlocal elasticity theory are employed for formulation of the problem. The equations of motion are derived using Hamilton's principals by calculating kinetic energy, strain energy and work due to viscoelastic foundation. The effects of various parameters such as wavenumber, non-homogeneous index, nonlocal parameter and three parameters of foundation are performed on the phase velocity of the nanobeam. The obtained results indicate that some parameters such as non-homogeneous index, nonlocal parameter and wavenumber have significant effect on the response of the system.
Theoretical and Applied Mechanics Letters 2017, 7(3): 152-158.
doi: 10.1016/j.taml.2017.03.001
Abstract:
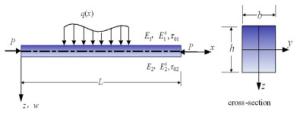
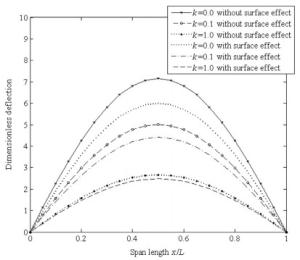
The bending responses of functionally graded (FG) nanobeams with simply supported edges are investigated based on Timoshenko beam theory in this article. The Gurtin-Murdoch surface elasticity theory is adopted to analyze the influences of surface stress on bending response of FG nanobeam. The material properties are assumed to vary along the thickness of FG nanobeam in power law. The bending governing equations are derived by using the minimum total potential energy principle and explicit formulas are derived for rotation angle and deflection of nanobeams with surface effects. Illustrative examples are implemented to give the bending deformation of FG nanobeam. The influences of the aspect ratio, gradient index, and surface stress on dimensionless deflection are discussed in detail.
The bending responses of functionally graded (FG) nanobeams with simply supported edges are investigated based on Timoshenko beam theory in this article. The Gurtin-Murdoch surface elasticity theory is adopted to analyze the influences of surface stress on bending response of FG nanobeam. The material properties are assumed to vary along the thickness of FG nanobeam in power law. The bending governing equations are derived by using the minimum total potential energy principle and explicit formulas are derived for rotation angle and deflection of nanobeams with surface effects. Illustrative examples are implemented to give the bending deformation of FG nanobeam. The influences of the aspect ratio, gradient index, and surface stress on dimensionless deflection are discussed in detail.
Theoretical and Applied Mechanics Letters 2017, 7(3): 169-174.
doi: 10.1016/j.taml.2017.03.004
Abstract:
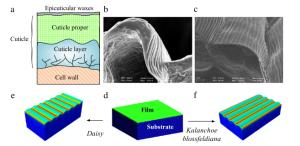
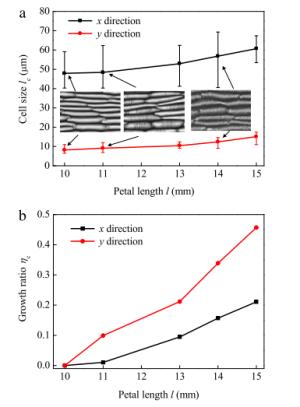
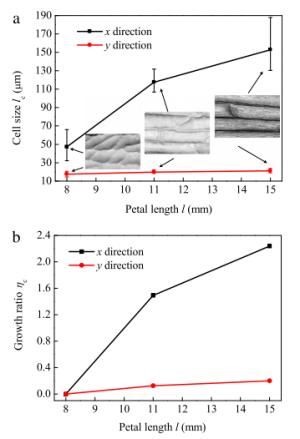
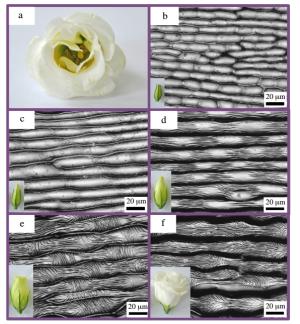
Flower petals have not only diverse macroscopic morphologies but are rich in microscopic surface patterns, which are crucial to their biological functions. Both experimental measurements and theoretical analysis are conducted to reveal the physical mechanisms underlying the formation of minute wrinkles on flower petals. Three representative flowers, daisy, kalanchoe blossfeldiana, and Eustoma grandiflorum, are investigated as examples. A surface wrinkling model, incorporating the measured mechanical properties and growth ratio, is used to elucidate the difference in their surface morphologies. The mismatch between the anisotropic epidermal cell growth and the isotropic secretion of surficial wax is found to dictate the surface patterns.
Flower petals have not only diverse macroscopic morphologies but are rich in microscopic surface patterns, which are crucial to their biological functions. Both experimental measurements and theoretical analysis are conducted to reveal the physical mechanisms underlying the formation of minute wrinkles on flower petals. Three representative flowers, daisy, kalanchoe blossfeldiana, and Eustoma grandiflorum, are investigated as examples. A surface wrinkling model, incorporating the measured mechanical properties and growth ratio, is used to elucidate the difference in their surface morphologies. The mismatch between the anisotropic epidermal cell growth and the isotropic secretion of surficial wax is found to dictate the surface patterns.
Theoretical and Applied Mechanics Letters 2017, 7(3): 159-163.
doi: 10.1016/j.taml.2017.04.001
Abstract:
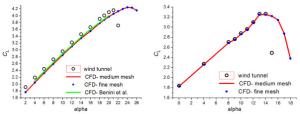
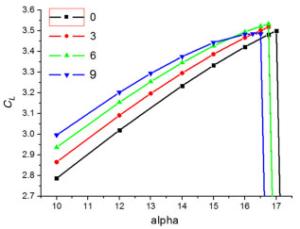
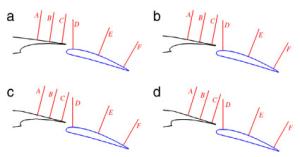
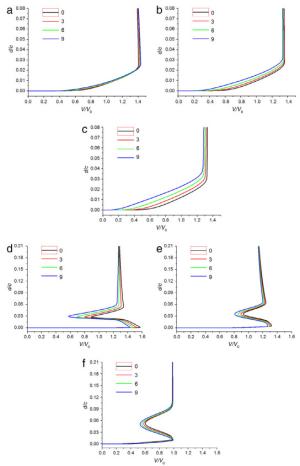
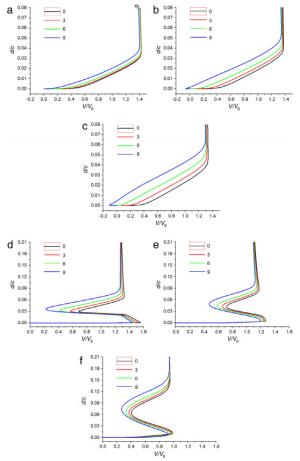
This paper numerically studies the influence of the downward spoiler deflection on the boundary layer flow of a high-lift two-element airfoil consisting of a droop nose, a main wing, a downward deflecting spoiler and a single slotted flap. Both of the boundary layer of the upper surface of the spoiler and the confluent boundary layer of the upper surface of the flap become thicker, as the downward spoiler deflection increases. Compared to the attached flow at the angle of attack of 10°, the flow of the upper surface of the spoiler becomes separated at the angle of attack of 16° when the spoiler deflection is large enough, which corresponds to the boundary layer flow reversal in velocity profiles.
This paper numerically studies the influence of the downward spoiler deflection on the boundary layer flow of a high-lift two-element airfoil consisting of a droop nose, a main wing, a downward deflecting spoiler and a single slotted flap. Both of the boundary layer of the upper surface of the spoiler and the confluent boundary layer of the upper surface of the flap become thicker, as the downward spoiler deflection increases. Compared to the attached flow at the angle of attack of 10°, the flow of the upper surface of the spoiler becomes separated at the angle of attack of 16° when the spoiler deflection is large enough, which corresponds to the boundary layer flow reversal in velocity profiles.
Theoretical and Applied Mechanics Letters 2017, 7(3): 164-168.
doi: 10.1016/j.taml.2017.05.004
Abstract:
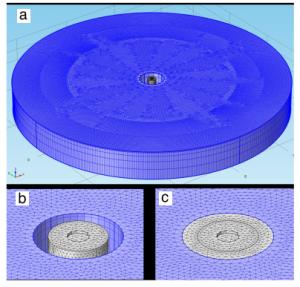
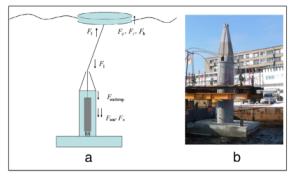
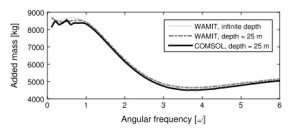
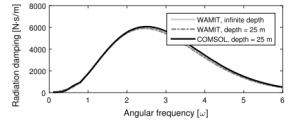
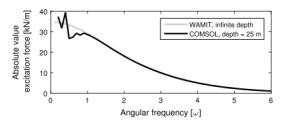
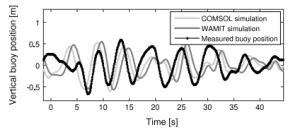
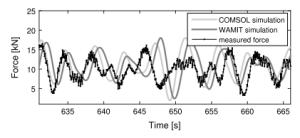
When designing a wave power plant, reliable and fast simulation tools are required. Computational fluid dynamics (CFD) software provides high accuracy but with a very high computational cost, and in operational, moderate sea states, linear potential flow theories may be sufficient to model the hydrodynamics. In this paper, a model is built in COMSOL Multiphysics to solve for the hydrodynamic parameters of a point-absorbing wave energy device. The results are compared with a linear model where the hydrodynamical parameters are computed using WAMIT, and to experimental results from the Lysekil research site. The agreement with experimental data is good for both numerical models.
When designing a wave power plant, reliable and fast simulation tools are required. Computational fluid dynamics (CFD) software provides high accuracy but with a very high computational cost, and in operational, moderate sea states, linear potential flow theories may be sufficient to model the hydrodynamics. In this paper, a model is built in COMSOL Multiphysics to solve for the hydrodynamic parameters of a point-absorbing wave energy device. The results are compared with a linear model where the hydrodynamical parameters are computed using WAMIT, and to experimental results from the Lysekil research site. The agreement with experimental data is good for both numerical models.
Theoretical and Applied Mechanics Letters 2017, 7(3): 175-178.
doi: 10.1016/j.taml.2017.05.005
Abstract:
The main objective for this research was the analytical exploration of the dynamics of planar satellite rotation during the motion of an elliptical orbit around a planet. First, we revisit the results of J. Wisdom et al. (1984), in which, by the elegant change of variables (considering the true anomaly f as the independent variable), the governing equation of satellite rotation takes the form of an Abel ordinary differential equation (ODE) of the second kind, a sort of generalization of the Riccati ODE. We note that due to the special character of solutions of a Riccati-type ODE, there exists the possibility of sudden jumping in the magnitude of the solution at some moment of time. In the physical sense, this jumping of the Riccati-type solutions of the governing ODE could be associated with the effect of sudden acceleration/deceleration in the satellite rotation around the chosen principle axis at a definite moment of parametric time. This means that there exists not only a chaotic satellite rotation regime (as per the results of J. Wisdom et al. (1984)), but a kind of gradient catastrophe (Arnold, 1992) could occur during the satellite rotation process. We especially note that if a gradient catastrophe could occur, this does not mean that it must occur:such a possibility depends on the initial conditions. In addition, we obtained asymptotical solutions that manifest a quasi-periodic character even with the strong simplifying assumptions e → 0, p=1, which reduce the governing equation of J. Wisdom et al. (1984) to a kind of Beletskii's equation.
The main objective for this research was the analytical exploration of the dynamics of planar satellite rotation during the motion of an elliptical orbit around a planet. First, we revisit the results of J. Wisdom et al. (1984), in which, by the elegant change of variables (considering the true anomaly f as the independent variable), the governing equation of satellite rotation takes the form of an Abel ordinary differential equation (ODE) of the second kind, a sort of generalization of the Riccati ODE. We note that due to the special character of solutions of a Riccati-type ODE, there exists the possibility of sudden jumping in the magnitude of the solution at some moment of time. In the physical sense, this jumping of the Riccati-type solutions of the governing ODE could be associated with the effect of sudden acceleration/deceleration in the satellite rotation around the chosen principle axis at a definite moment of parametric time. This means that there exists not only a chaotic satellite rotation regime (as per the results of J. Wisdom et al. (1984)), but a kind of gradient catastrophe (Arnold, 1992) could occur during the satellite rotation process. We especially note that if a gradient catastrophe could occur, this does not mean that it must occur:such a possibility depends on the initial conditions. In addition, we obtained asymptotical solutions that manifest a quasi-periodic character even with the strong simplifying assumptions e → 0, p=1, which reduce the governing equation of J. Wisdom et al. (1984) to a kind of Beletskii's equation.
 Submit a Paper
Submit a Paper
 Subscription
Subscription
News
MORE+
Call for Papers
MORE+
- Crossing-Mechanics Driven by Big Data
- Machine learning in the fluid mechanics research of wind energy
- Mechanics of Origami/Kirigami structures and metamaterials
- New insights and perspectives on impact biomechanics for human tissues: from injury prevention, protection to protective equipment
- Environmental Mechanics for Extreme Natural Events